9.2: Forces on Bed Particles
- Page ID
- 4205
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Look at a representative sediment particle resting on the surface of a cohesionless sediment bed at the bottom of a flowing fluid (Figure \(\PageIndex{1}\)). If the fluid is not moving fast enough to move the particle, then the particle is motionless, therefore not accelerating, so all the forces acting on it must be in balance. What are those forces? They are of three kinds: particle weight, particle-to-particle contact forces, and fluid forces.
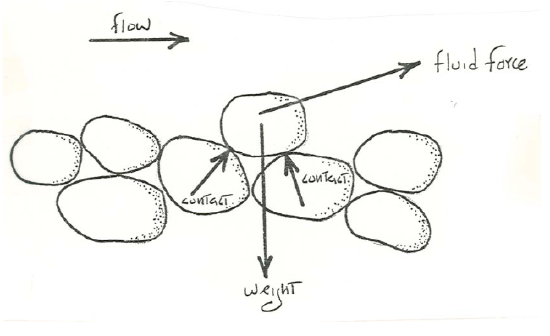
The particle weight is easy to deal with: it is just the submerged weight per unit volume of the sediment material, \(\gamma^{\prime}\), times the volume of the particle. It acts vertically downward through the center of mass of the particle. The contact forces, exerted upward on the given particle by the underlying particles (usually three) on which it rests, become adjusted in light of the contact geometry, the particle weight, and the fluid forces so that the particle is motionless.
The fluid forces are much more difficult to deal with. First we need a little more background on the nature of flow very near the bed in a turbulent shear flow.
Fluid Forces
Because there is locally a flow around the bed particle, you should expect there to be both viscous shear stresses and pressure acting at every point of the surface of the particle (Figure \(\PageIndex{2}\)). It is those viscous and pressure forces, summed over the entire surface of the particle, that give rise to the resultant fluid force on the particle. This resultant force is specified by its magnitude, direction, and line of action through the particle.
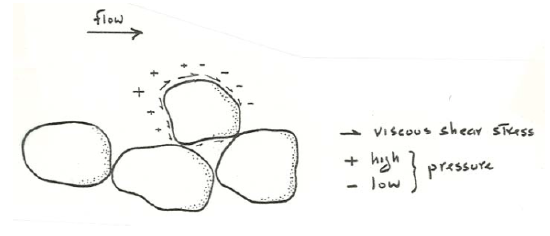
Keep in mind that if the flow is turbulent, which is almost always the case in problems of sedimentological interest, the resultant force varies strongly with time, on time scales ranging from small fractions of a second to many minutes (in the case of very large-scale flows, in which the maximum eddy size can be very large), even if the flow is steady in the time-average sense. And this is true even if the particle is within the viscous sublayer. Remember that the viscous sublayer is not really nonturbulent: the local velocity fluctuates substantially within it. The important point is that the turbulence is unimportant in contributing turbulent shear stress to the total shear stress in the viscous sublayer. You can readily understand the existence of velocity fluctuations in the viscous sublayer in the context of the burst–sweep cycle described in Chapter 4: the viscous sublayer is thinned and accelerated as masses of high-speed fluid impinge on the bed, and then it thickens and decelerates again.
What determines the magnitude, distribution, and relative importance of the viscous and pressure forces? Think about the variables that govern the fluid force on a bed particle. Some should come to mind readily: the diameter \(D\) of the particle (which determines the surface area of the particle, and also how far up into the flow the particle projects), the fluid viscosity \(\mu\) (viscous stresses are important); the fluid density \(\rho\) (fluid is accelerating in the vicinity of the particle); the boundary shear stress \(\tau_{\text{o}}\) (that is the variable that best characterizes the strength of the flow around the particle); and the geometry of the particle itself and its relationship to underlying particles. The geometry varies widely—it is different for each particle—but, for any given particle, the other variables lead naturally to a single dimensionless variable \(\rho u_{*}D / \mu\), which you have already seen in Chapter 4 as the boundary Reynolds number.
A further comment about the boundary shear stress is in order here. It is not the boundary shear stress, as carefully defined in Chapter 4 as the time-average force per unit area on the bed, averaged over an area of the bed that is large enough to guarantee a representative spatial average, that is directly relevant to threshold of movement; it is the picture of local fluid forces on individual bed particles and how those forces vary with time. Nonetheless, \(\tau_{\text{o}}\) is a good descriptor of the threshold condition for movement, because it represents the average of the forces on the bed particles. There is an important qualification to that statement, however: the bed has to be planar in the large, without any features like bed forms that are much larger than the particles themselves, or otherwise much or most of the bed shear stress is associated with form drag rather than with the skin friction, which is what actually moves the particles.
Figure \(\PageIndex{3}\) shows in a qualitative way how the fluid force on a given particle should vary with the boundary Reynolds number \(\text{Re}_{*}\).
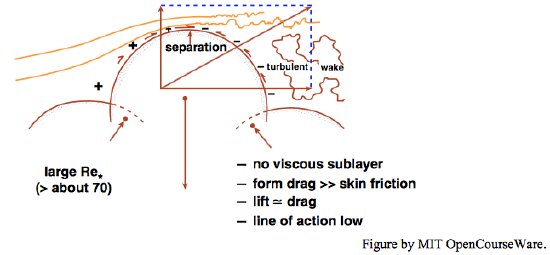
- For small \(\bf{Re}_{*}\) (which corresponds to relatively small values of a Reynolds number based on local flow velocity around the particle) there is no well defined boundary layer along the top surface of the particle, and there is no flow separation behind the particle (Figure \(\PageIndex{3}\)A). Both viscous forces and pressure forces are important. The line of action of the resultant force lies well above the center of mass of the particle, because the viscous forces are strongest on the uppermost surface of the particle.
- For large \(\bf{Re}_{*}\) (which corresponds to relatively large values of a Reynolds number based on local flow velocity) there is a well defined local boundary layer on the surface of the particle, and pronounced flow separation, with a turbulent wake behind the particle (Figure \(\PageIndex{3}\)B). Pressure forces far outweigh viscous forces, and because the net pressure force comes about mainly by the difference in pressure from front to back the line of action of the resultant force is closer to the center of mass of the particle.
There is no reason to expect the resultant force to be parallel to the overall surface of the bed; this leads to the idea of resolving the resultant force into a component parallel to the bed, called the drag, and a component normal to the bed, called the lift (Figure \(\PageIndex{4}\)). Several investigators, using sometimes ingenious experimental methods, have attempted to make direct measurements of the lift and drag forces on bed particles (or surrogates, like regularly spaced hemispheres on a planar boundary); see Einstein and El-Samni (1949), Chepil (1958, 1961), Coleman (1967), and Coleman and Ellis (1976).
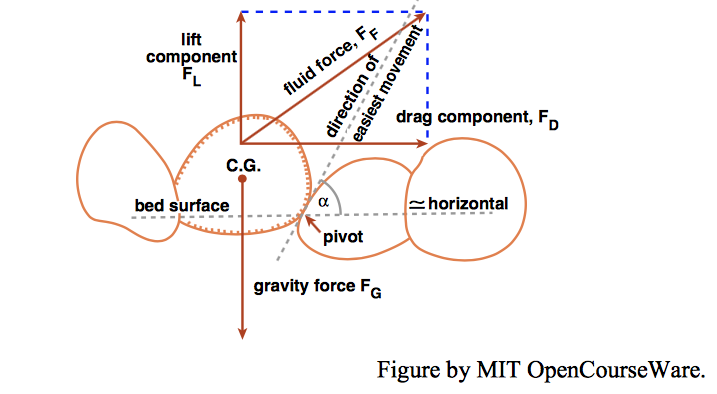
A lift force on the particle is to be expected because the pressure is high around the base of the particle (the front stagnation point is located low on the front surface of the particle), and relatively low over the top surface of the particle, as well as in the rear; to see that, all you have to do is apply the Bernoulli equation qualitatively. People have made ingenious experiments to measure the lift force, and the lift force has been found to be almost equal to the drag force at high boundary Reynolds numbers. There is some evidence that at very low Reynolds numbers the lift force actually becomes weakly negative, for reasons no one seems to understand very well yet.
Another important thing you should expect about the fluid force is that it is extremely unsteady, because of fluctuations in velocity associated with the passage of fairly large eddies just outside the near-boundary layer of the flow. Actual measurements have shown fluctuations by as much as a factor of four in the instantaneous fluid forces on bed particles.


