5.5.2: Radiation Stress
- Page ID
- 16327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Newton’s second law states that the rate of change of momentum of a fluid element equals the forces on the element. Waves can change the momentum through net ‘inflow’ or ‘outflow’ of momentum, either by net inflow or outflow of momentum with the particle velocity or via a net wave-induced pressure force. Radiation stress is the name that has been given to the depth-integrated and wave-averaged flow (or flux) of momentum due to waves. It was first defined by Longuet-Higgins and Stewart (1964) as the excess momentum flux due to the presence of waves.
If there is change in wave-induced momentum flux (radiation stress) from one location to another, wave forces act on the fluid, impacting mean water motion and levels. These wave forces are responsible for:
- lowering the mean water level in the shoaling zone (set-down);
- raising the mean water level in the surf zone (set-up);
- driving a longshore current in the case of waves obliquely approaching the shore (1 m/s under some conditions).
Definition of radiation stress components
The wave-induced horizontal flux of momentum through a vertical plane at a given location consists of:
- the transfer of momentum \(\rho \vec{u}\) through that plane with the particle velocity normal to that plane;
- the wave-induced pressure force acting on the plane due to the wave induced pressure \(p_{\text{wave}}\) in the water.
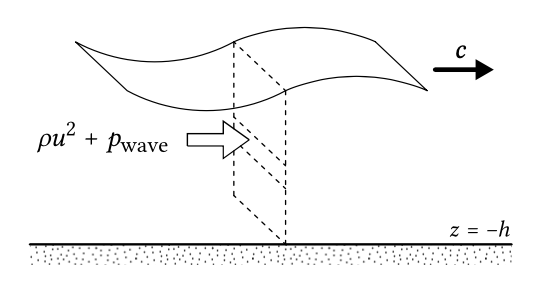
First assume that the plane under consideration is perpendicular to the wave propagation (Fig. 5.27). The wave-induced pressure \(p_{\text{wave}}\) acts by definition normal to the plane. Besides, at every height above the bed the particle velocity \(u\) transports momentum \(\rho u\) through the plane (per unit crest length).

Figure 5.28: Coordinate system and velocity vector.
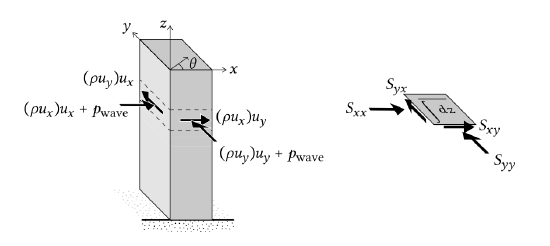
Figure 5.29: Schematic of the momentum transport and radiation stress components at a certain point in \(x,y\)-space for obliquely incident waves. The radiation stresses are obtained by integration of the momentum transport over the water column and averaging in time.
Now consider a coordinate system according to Fig. 5.28. The wave propagates at an angle with the \(x\)-axis. The particle velocity has a component \(u_x\) in the \(x\)-direction and a component \(u_y\) in the \(y\)-direction. The particle velocity \(u_x\) transports both \(x\)-momentum \(\rho u_x\) and \(y\)-momentum \(\rho u_y\). The transport of \(x\)-momentum by the particle velocity \(u_x\) through a vertical plane perpendicular to the \(x\)-axis (per unit time and per unit area) is \((\rho u_x) u_x\) and the transport of \(y\)-momentum through the plane is \((\rho u_y) u_x\). The momentum fluxes can be seen in the left part of Fig. 5.29).
Figure 5.29 visualises the momentum transport and radiation stress components in \(x\)-direction and \(y\)-direction at a certain point in \(x,y\)-space. The momentum transport through the entire plane per unit crest length is obtained by integration over the depth from bottom to instantaneous water surface. Time-averaging yields for the total wave-averaged transport of \(x\)-momentum in the \(x\)-direction or the radiation stress \(S_{xx}\):
\[S_{xx} = \underbrace{\overline{\int_{-h_0}^{\eta} (\rho u_x) u_x dz}}_{\text{part due to advection by horizontal particle velocity}} + \underbrace{\overline{\int_{-h_0}^{\eta} p_{\text{wave}} dz}}_{\text{pressure part}}\label{eq5.5.2.1}\]
\(S_{xx}\) acts normal to the considered plane and is therefore a normal component of the radiation stress. It is equivalent to a normal stress acting in the \(x\)-direction.
The radiation stress component \(S_{xy}\) (the shear component of the radiation stress) is defined as the transport of \(x\)-momentum in the \(y\)-direction. It acts as a shear stress on the plane (it is directed in the \(x\)-direction, and works on the plane normal to the \(y\)-direction) and is given by:
\[S_{xy} = \overline{\int_{-h_0}^{\eta} (\rho u_x) u_y + \tau_{xy} dz}\]
The shear stress due to waves is zero for an irrotational ideal fluid so that we have:
\[S_{xy} = \overline{\int_{-h_0}^{\eta} (\rho u_x) u_y dz} \label{eq5.5.2.3}\]
It consists of a contribution due to advection by the horizontal orbital velocity only. Note that for the special case of normally incident waves the \(x\)-direction is the wave propagation direction, and \(u_y\) and hence \(S_{xy}\) are zero.
Considering a plane normal to the \(y\)-direction, we find for the momentum fluxes in the \(y\)-direction, the normal component:
\[S_{yy} = \underbrace{\overline{\int_{-h_0}^{\eta} (\rho u_y) u_y dz}}_{\text{part due to advection by horizontal particle velocity}} + \underbrace{\overline{\int_{-h_0}^{\eta} p_{\text{wave}} dz}}_{\text{pressure part}}\]
and the shear component:
\[S_{yx} = \overline{\int_{-h_0}^{\eta} (\rho u_y) u_x dz} \label{eq5.5.2.5}\]
In the special case that the \(x\)-direction is the wave propagation direction \(u_y = 0, S_{yy}\) reduces to the pressure part and \(S_{yx} = S_{xy} = 0\).
Radiation stress expressions using linear wave theory
By using linear (first order) wave theory, expressions for the radiation stress can be obtained that are valid to second order. The complete derivation can be found in Holthuijsen (2007). Intermezzo 5.4 gives an excerpt of this derivation.
It is easiest to start from a wave propagating in positive \(x\)-direction so that \(u_x = u\) and \(u_y = 0\). If we substitute \(u = \hat{u} \cos (\omega t - kx)\) with \(\hat{u}\) according to Sect. 5.4.1 in the particle velocity part of Eq. \(\ref{5.5.2.1}\) we find (see Holthuijsen (2007) for the derivation):
\[S_{xx, \text{horizontal particle velocity}} = \overline{\int_{-h_0}^{\eta} (\rho u^2) dz} \approx \int_{-h_0}^{0} \rho \overline{u^2} dz = nE\]
where:
| \(S_{xx}, \text{hor, part, vel.}\) | radiation stress in the wave propagation direction due to advection of momentum by the horizontal orbital motion | \(N/m\) |
| \(n\) | ratio of group velocity and phase velocity | - |
| \(E\) | wave energy in the water column per \(m^2\) | \(J/m^2\) |
In the case of irregular waves this equation can be applied using \(E = 1/8 \rho g H_{rms}^2\). For the mass flux we found a zero contribution for every level below the wave trough because \(\bar{u} = 0\). The momentum flux however is non-zero for the entire water depth since \(\overline{u^2} \ne 0\). It varies in principle over the depth. Only in shallow water, where the horizontal orbital velocity is uniformly distributed, the particle velocity part of the radiation stress is uniformly distributed.
The pressure for any level below the trough would give a zero time-averaged result according to linear theory. There is however a contribution to the time-averaged wave-induced pressure \(\overline{p_{\text{wave}}}\) due to the vertical flux of momentum by the vertical fluid motion. This may be thought of as the vertical oscillatory fluid motion helping carry the weight of the water column and is given by \(-\rho \overline{w^2}\), in which \(w\) is the vertical orbital velocity. The contribution to the radiation stress can be found by substituting the linear expression for \(w\) and integrate to the mean water level. We find:
\[S_{xx, \text{pressure, 1}} = -\overline{\int_{-h_0}^{\bar{\eta}} \rho w^2 dz} \approx -\int_{-h_0}^{0} \rho \overline{w^2} dz = (n - 1)E\]
Besides, there is a contribution to the radiation stress due to the pressure fluctuations between wave trough and wave crest level. In Sect. 5.4.2 we assumed that the pressure between wave trough and crest level fluctuates as \(\tilde{p} = \rho g \eta\). This gives the following net contribution to the radiation stress:
\[S_{xx, \text{pressure, 2}} = \overline{\int_{0}^{\bar{\eta}} \rho g \eta dz} = \dfrac{1}{2} \rho g \overline{\eta^2} = \dfrac{1}{2} E \label{eq5.5.2.8}\]
This gives for the pressure part of the radiation stresses:
\[S_{xx, \text{pressure}} = \underbrace{(n - 1)E}_{\text{contribution due to (depth-varying) vertical momentum flux}} + \underbrace{1/2 E}_{\text{contribution at top of water column}} = (n - 1/2) E\label{eq5.5.2.9}\]
The term \(\overline{w^2}\) varies in principle with the water depth, whereas the other part (from Eq. \(\ref{eq5.5.2.8}\)) is located at the top of the water column. In shallow water (\(n = 1\)) the vertical orbital velocities are zero and the pressure part of the radiation stresses reduces to a contribution \(S_{xx, \text{pressure}} = 1/2 E\) at the top of the water column. In deep water where \(n = 1/2\) the pressure component to the radiation stress is \((n - 1/2) E\).
The total radiation stress in the wave propagation direction (\(x\)-direction) is now:
\[S_{xx} = S_{xx, \text{pressure}} + S_{xx, \text{horizontal particle velocity}} = (n -1/2) E + nE \label{eq5.5.2.10}\]
The stresses normal to the wave propagation direction \(S_{yy}\) consist of the pressure part \((n - 1/2) E\) only. The shear stresses are zero.
From Intermezzo 5.4 – or more specifically from Eq. \(\ref{eq5.5.2.10}\) – we conclude that:
- The pressure part of the radiation stress is equal to \((n - 1/2) E\). Since pressure is a scalar this term is part of radiation normal stresses in all directions.
- The magnitude of the advective part of the radiation stress, the part due to transport of momentum by the particle velocity, is \(nE\). It is by definition in the wave propagation direction.
With this result, we can now deduce the more general expressions for the radiation stress components for waves travelling in a direction \(\theta\) relative to the positive \(x\)-direction (see Fig. 5.28). If the \(x\)-axis is not the propagation direction we have \(\vec{u} = (u_x , u_y) = (u \cos \theta, u \sin \theta)\) and with Eqs. \(\ref{eq5.5.2.1}\), \(\ref{eq5.5.2.3}\) and \(\ref{eq5.5.2.5}\) we find:
\[S_{xx} = (n - \dfrac{1}{2} + n \cos^2 \theta) E \label{eq5.5.2.11}\]
\[S_{yy} = (n - \dfrac{1}{2} + n \sin^2 \theta) E\]
\[S_{xy} = S_{yx} = n \cos \theta \sin \theta E \label{eq5.5.2.13}\]
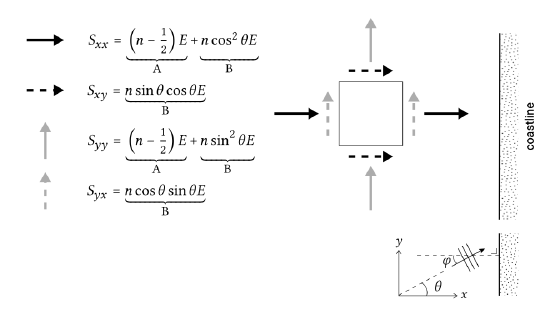
In the situation of an alongshore uniform coast, the positive \(x\)-direction is generally taken as the shore-normal direction and the positive \(y\)-direction is parallel to the coast-line. The angle of incidence of the wave \(\varphi\) with respect to the depth contours is now equal to the angle \(\theta\) with the positive \(x\)-axis. For that situation, the radiation stress components are sketched in Fig. 5.30.
Note that if the \(x\)-axis coincides with the wave propagation direction ( = 0), the above Eqs. \(\ref{eq5.5.2.11}\) to \(\ref{eq5.5.2.13}\) reduce to:
\[S_{xx} = (2n - 1/2) E\]
\[S_{yy} = (n - 1/2) E \ \ \text{for waves propagating in the } x\text{-dircetion}\]
\[S_{xy} = S_{yx} = 0\]
This is in accordance with the earlier findings that:
- The normal stresses perpendicular to the direction of wave propagation consist of the pressure part \((n - 1/2) E\) only;
- The normal stresses in the direction of wave propagation consist of the pressure part \((n - 1/2) E\) plus the part due to momentum transfer by the horizontal orbital motion \(n E\);
- The shear stresses are zero if the \(x\)-direction is the direction of wave propagation.
In deep water where \(n = 1/2\), the pressure component to the radiation stress is \((n - 1/2)E = 0\) and the fluid particle part becomes \(n E = 1/2 E\) in the direction of wave propagation. Thus in the case of wave propagation in the \(x\)-direction, we find \(S_{xx} = 1/2 E\), and \(S_{yy} = 0\). In shallow water, on the other hand, where \(n = 1\), it follows that \(S_{xx} = 3/2 E\), and \(S_{yy} = 1/2 E\). Here both contributions add to the total radiation stress \(S_{xx}\) and \(S_{yy}\) is equal to the pressure part. The radiation (normal) stress in shallow water is clearly larger than in deep water. And, it has two components in shallow water: parallel and perpendicular to the direction of wave propagation.
Radiation stress in breaking waves
In breaking surf zone waves, the effect of the surface roller will be to delay the momentum release from the wave breaking. In practice this means that the equations for the radiation stresses will contain a term due to roller energy too. Different models exist for this term, enhancing either the pressure part or advection part of the radiation stress or both. Svendsen (1984) proposes an additional contribution to the radiation stress in the propagation direction due to the velocity in the roller by an amount \(q_{\text{roller}} c = \alpha E_r\) (see Eq. \(\ref{eq5.5.2.9}\)). This contribution is concentrated near the water surface where the wave breaking takes place. Under the assumption of shallow water, the radiation stress below the wave trough level is dominated by the part due to advection of momentum by the horizontal orbital motion (verify this from Intermezzo 5.4). Since in shallow water the horizontal orbital velocity is uniformly distributed, the advective part of the radiation stress is uniformly distributed as well.


