22.5: Diffraction and Interference
- Page ID
- 10981
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
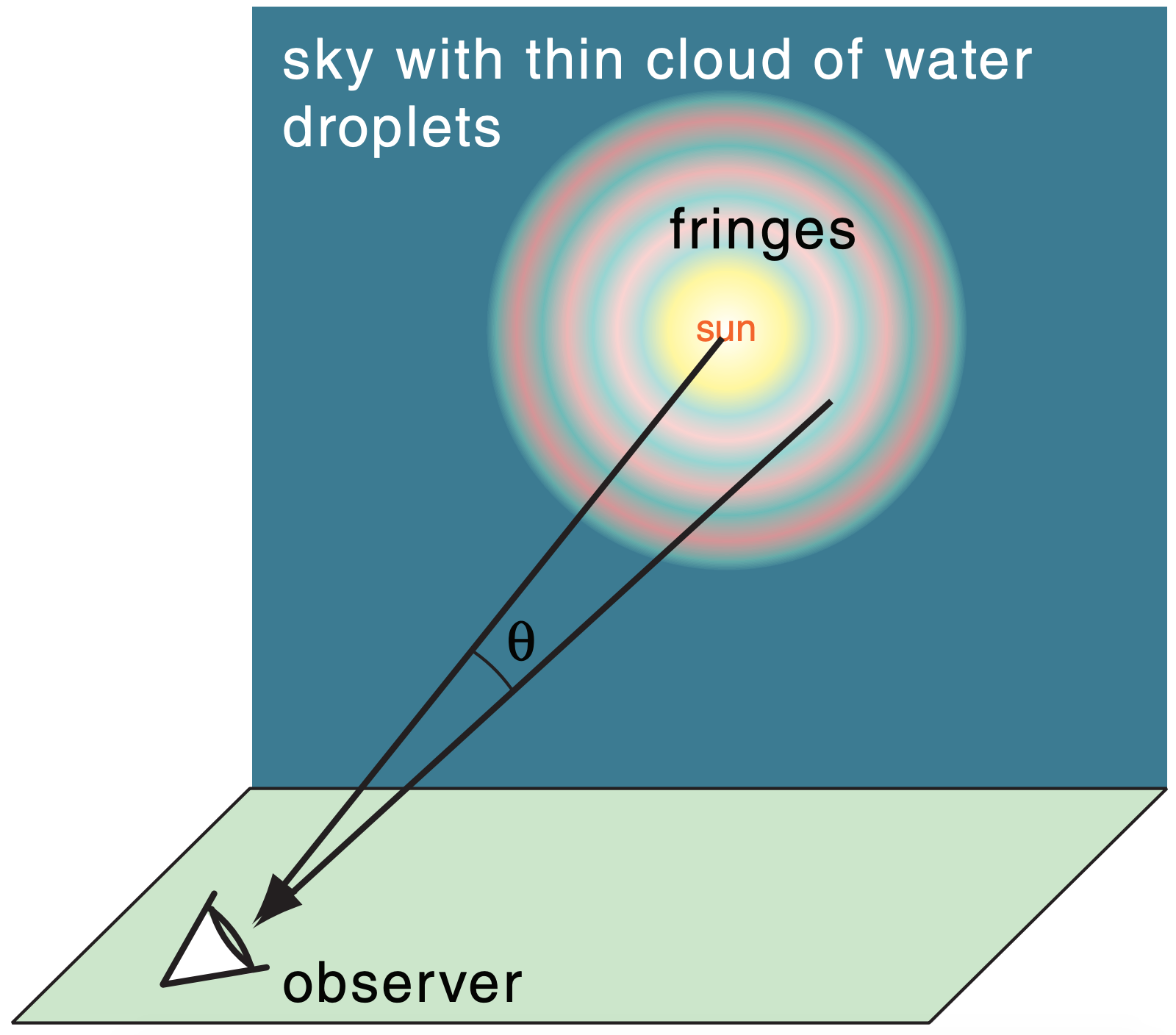
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When sunlight or moonlight passes through a thin cloud of water droplets, diffraction and interference can produce a disk of bright sky centered on the luminary (light source), surrounded by one or more colored rings or fringes (Fig. 22.48).
Recall from physics that when wave fronts hit the edge of an object, part of the wave bends around the edge — a process called diffraction. This is consistent with Huygens’ principle, where every point on an incident wave front can be thought of as a source of new wavelets radiating away, and where the subsequent position of the wave front depends on the superposition of the wavelets. An analogy is ocean waves moving past vertical posts or pilings.
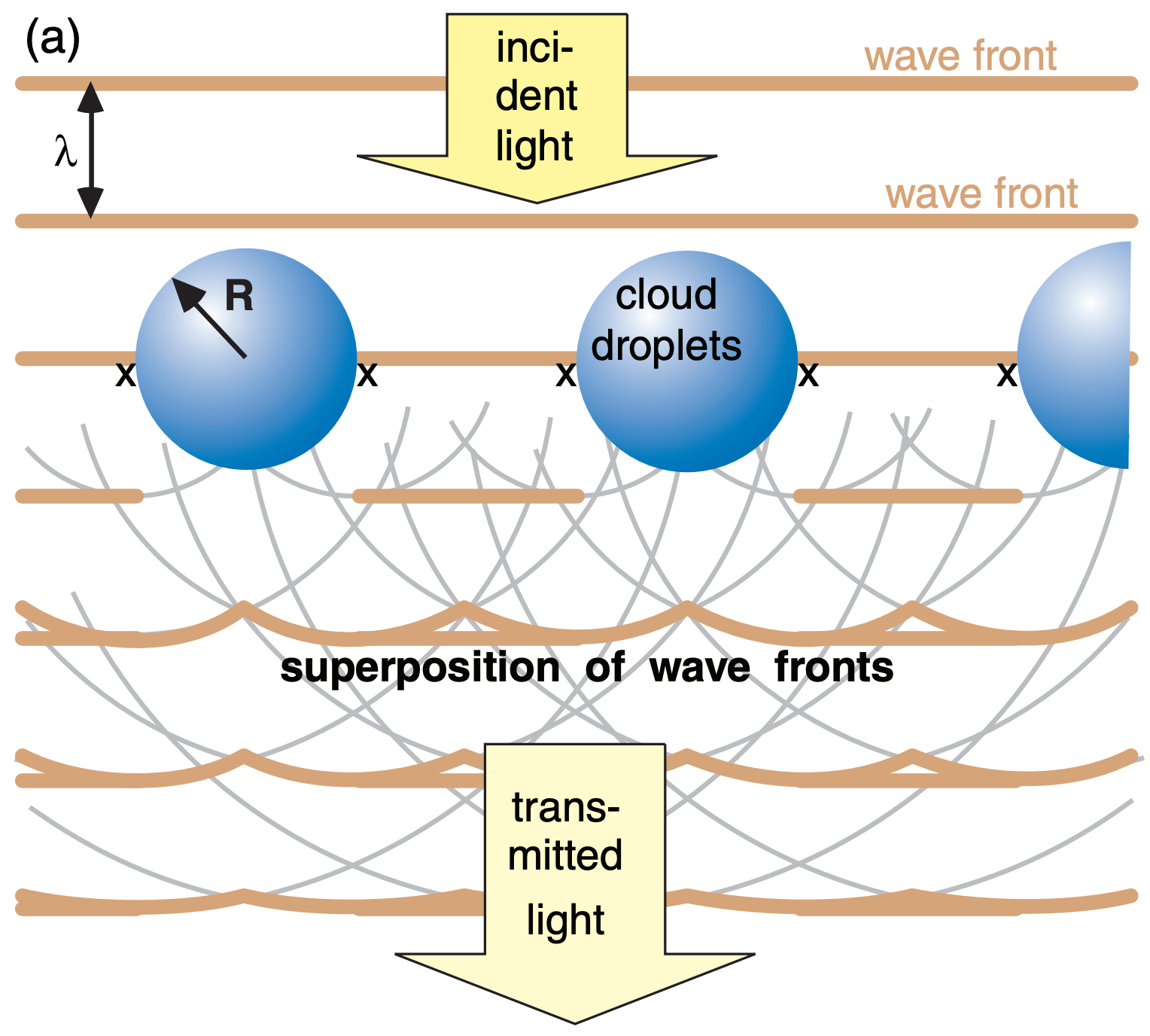
Fig. 22.49a sketches cloud droplets and the wave fronts of incident light from the sun or moon. The edge of each droplet is marked with an “x”. Consider the wavelets generated from each edge, sketched as the thin grey concentric circles. Superposition of these wavelets, indicated with the thick tan wavy line, can constructively interfere to create a new wave train. Fig. 22.49a shows one of the resulting wave trains — the one for light that is transmitted straight through the cloud to the observer. Other angles have destructive interference.
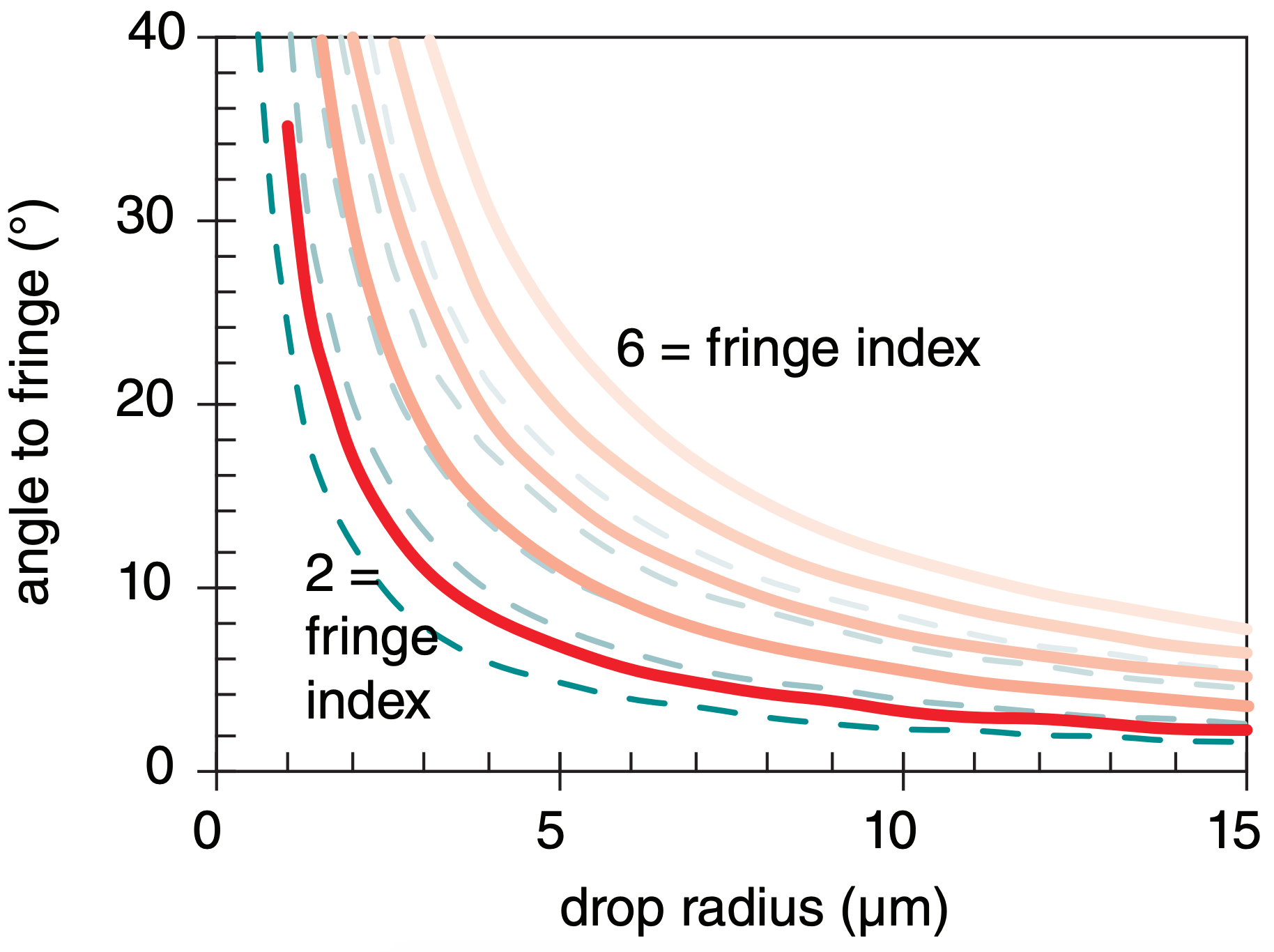
However, there are many other angles where the wavelet fronts constructively interfere, one of which is sketched in Fig. 22.49b. This has the net effect of producing an additional train of wave fronts that leaves the cloud at a different angle. Because this angle of light leaving the cloud is the same as the angle observed by the observer, the observer sees the constructive interference (i.e., bright light) from all those different drops that happen to be the same viewing angle away from the sun. The different angles that can be produced from a set of drops produces many rings of different radii, called fringes.
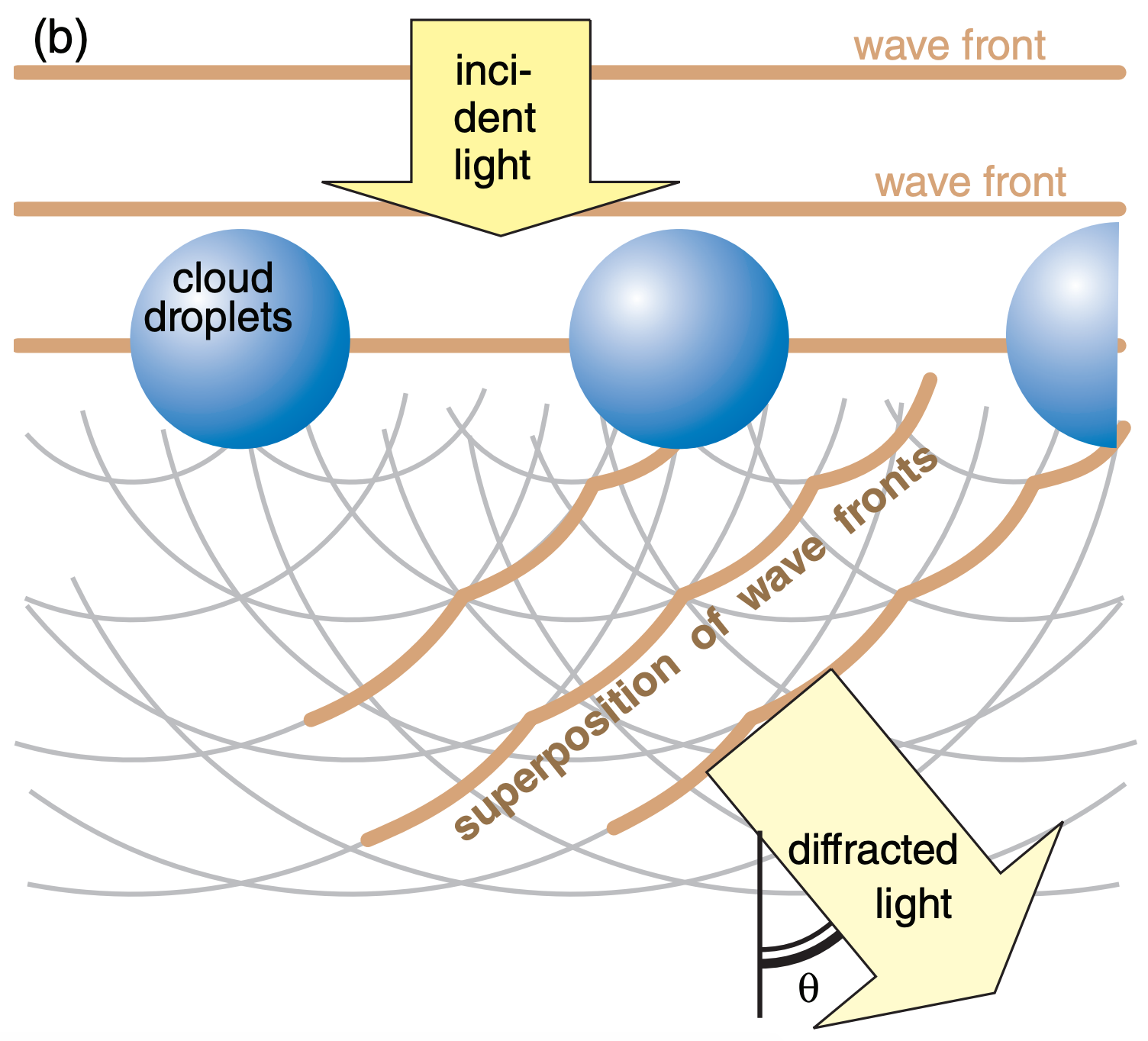
The angle θ to each ring depends on the radius R of the droplet and the wavelength λ of light:
\begin{align}\theta=\arcsin \left(\frac{m \cdot \lambda}{R}\right)\tag{22.23}\end{align}
where m is a dimensionless diffraction parameter given in Table 22-5.
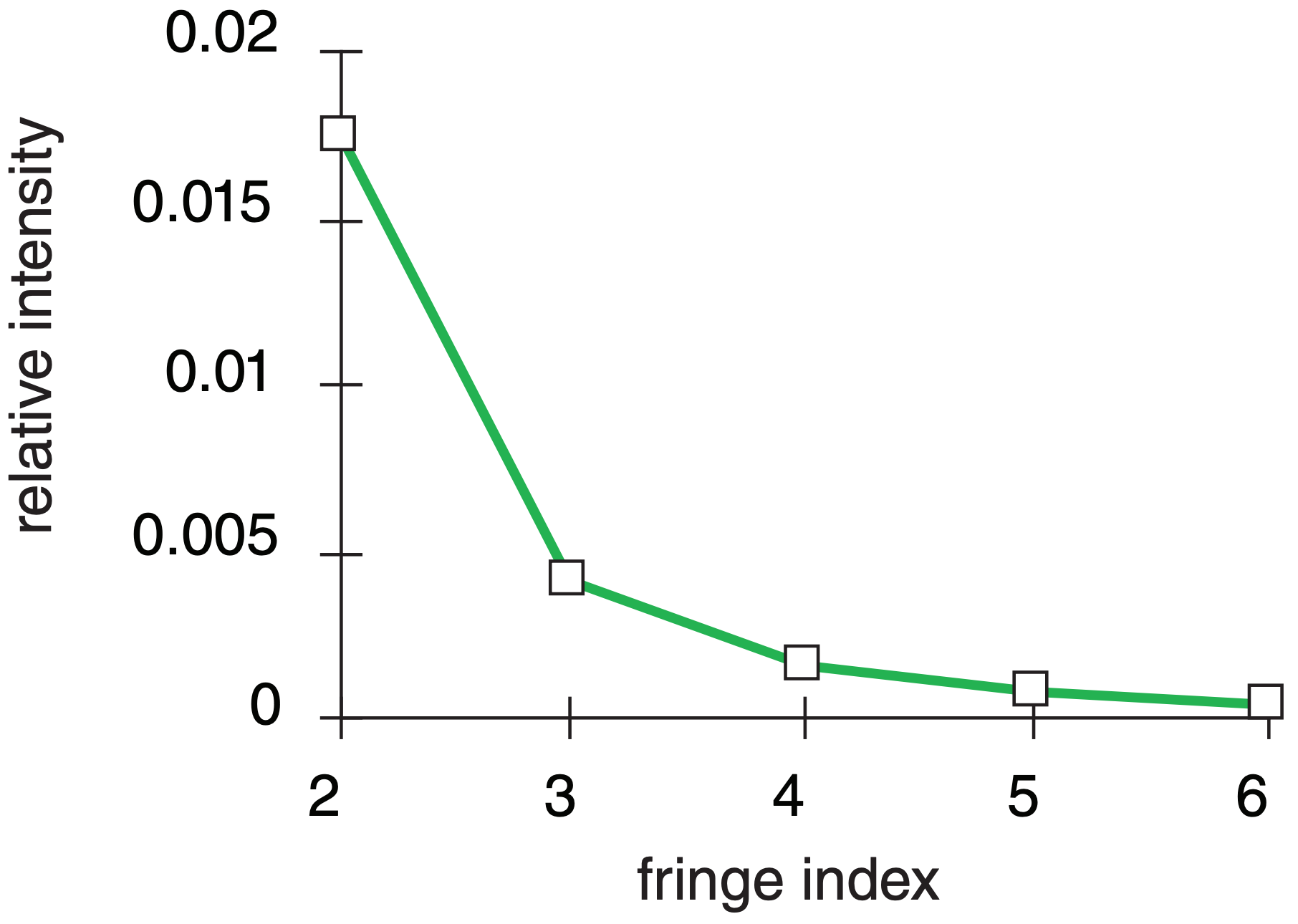
| Table 22-5. Diffraction fringes. | ||
| Fringe Index | m | Relative Intensity |
|---|---|---|
|
1 2 3 4 5 6 7 8 |
0 0.819 1.346 1.858 2.362 2.862 3.362 3.862 |
1.0 0.01745 0.00415 0.00165 0.00078 0.00043 0.00027 0.00018 |
For any one color, there are faint rings of light separated by darker gray background. The different colors of the spectrum have different fringe radii, causing the fringes of any one color (e.g. blue-green) to appear in the dark spaces between fringes of another color (e.g., red). Fringes further from the sun (with higher fringe index) are less bright, as given in Table 22-5 and plotted in Fig. 22.50.
22.5.1. Corona, Iridescence and Glory
Wave clouds (standing lenticular clouds) have extremely uniform drop sizes. This means that all the drops in the cloud produce the same fringe angles, for any one color. Hence, the diffraction from all the droplets reinforce each other to produce bright colorful fringes (rings) called corona. Most other clouds contain drops with a wide range of sizes, causing the colors to smear together to form a whitish disk (called an aureole) touching the sun or moon.
Eq. (22.23) can be solved on a spreadsheet for various cloud droplet sizes and colors. The results in Fig. 22.51 show that smaller droplets produce larger-diameter fringes. For reference, typical cloud droplets have 10 µm radii, and the viewing angle subtended by the sun is 0.534°.
To help discriminate between corona and halos, remember that corona are bright disks of light that touch the sun or moon, while halos have a dark region between the luminary and the halo ring. Also, corona are formed from liquid water droplets, while halos are formed from ice crystals.
Droplets near the edges of clouds (particularly wave clouds) can be very small as they form or evaporate, and can cause fringes of very large angular radius. As a result, the edges of clouds near the sun or moon are often colorful, a phenomenon called iridescence.
When looking down from above a cloud, diffraction patterns are sometimes seen around the shadow of the observer. This is called glory, and is associated with both diffraction and reflection from the cloud droplets. When viewed from an aircraft flying above the clouds, the glory is a circle of light centered on the shadow of the airplane.
Sample Application
The first visible fringe (index = 2) of red is 10° from the moon. What is the cloud drop radius?
Find the Answer
Given: θ = 10°, λ = 0.7 µm.
m = 0.819 from Table 19-3 for fringe #2.
Find: R = ? µm
Assume nair ≈ 1.0002753 for red light.
Rearrange eq. (22.23):
R=\frac{m \cdot \lambda}{\sin \theta}=\frac{0.819 \cdot(0.7 \mu \mathrm{m})}{\sin \left(10^{\circ}\right)}=\underline{\bf{3.3 \mu \mathrm{m}}}
Check: Units OK. Physics OK.
Agrees with Fig. 22.51.
Exposition: Smaller than typical cloud-droplet size, perhaps associated with a wave cloud.
22.5.2. Supernumerary Bows
As sketched in Fig. 22.7, supernumerary bows are closely spaced faint pinkish-purple and turquoise diffraction arcs touching the inside of the primary rainbow arc. The viewing-angle width of this bow (containing 2 to 4 sequences of fringes) is 1 to 2°. Supernumerary bows are most visible when the raindrop diameter is smaller than about 1 mm, during a rain shower when most of the falling drops have nearly the same size (i.e., a narrow drop-size distribution).
When the rain shower has a wider drop-size distribution, the greater flattening of the larger drops causes many drops to have nearly the same vertical thickness, even though their horizontal diameters vary widely. Thus, supernumerary bows are often most visible inside the top of the rainbow arc (because drops of equal vertical thickness cause equal diffraction fringes that constructively interfere), and less visible inside the sides. Rainbows and supernumerary bows are also visible when the sun shines on dew drops on grass, and in water sprays from irrigation systems. Very faint supernumerary bows can sometimes be seen outside the secondary rainbow.
To explain the optics, look at Fig. 22.13b and consider red light at viewing angle 40°, for example. We see that light at this viewing angle comes from two different paths through the raindrop: one at impact parameter 0.74 and the other at impact parameter 0.94. These two different paths travel different distances through the drop, hence their wave fronts can get out of phase with each other. At certain angles for certain colors the wave fronts interfere with each other, canceling to yield no light of that color. At other angles for other colors, the wave fronts are in phase and reinforce each other, yielding a bright color. This constructive and destructive interference of wave fronts creates supernumeraries.


