14.10: Homework Exercises
- Page ID
- 10245
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)14.10.1. Broaden Knowledge & Comprehension
B1. Search the internet for (and print the best examples of) photographs of:
- airmass thunderstorms
- multicell thunderstorms
- orographic thunderstorms
- squall-line thunderstorms
- supercell thunderstorms
- classic
- low precipitation
- high precipitation
- mammatus clouds
- wall clouds
- beaver tail clouds
- flanking lines
- tail cloud
(Hint: search on “storm stock images photographs”.) Discuss the features of your resulting image(s) with respect to information you learned in this chapter.
B2. Search the internet for (and print the best examples of) radar reflectivity images of
- airmass thunderstorms
- multicell thunderstorms
- squall line thunderstorms
- mesoscale convective systems
- bow echoes
Discuss the features of your resulting image(s) with respect to information you learned in this chapter.
B3. Same as the previous question, but for radar Doppler velocity images.
B4. Search the internet for (and print the best examples of) satellite images of:
- airmass thunderstorms
- multicell thunderstorms
- squall line thunderstorms
- mesoscale convective systems
- dry lines
Do this for visible, IR, and water vapor channels. Discuss the features of your resulting image(s) with respect to information you learned in this chapter.
B5. Search the internet for plotted soundings. In particular, find web sites that also list the values of key stability indices and key altitudes along with the sounding. From this site, get a sounding for a location in the pre-storm environment toward which thunderstorms are moving. Print the sounding and the stability indices, and use the sounding and indices to discuss the likelihood and severity of thunderstorms. (Hint: To find regions where thunderstorms are likely, first search the web for a weather radar image showing where the thunderstorms are. Alternately, find via web search the regions where the weather service has issued thunderstorm watches.)
B6. Search the internet for plotted hodographs. (Hint: Some sites plot hodographs along with plotted soundings, while others have separate hodograph plots.) Find a web site that also shows key windshear parameters associated with the hodograph, and perhaps also gives expected storm motion and/ or storm-relative winds. Do this for a location into which thunderstorms are moving (see hint from previous exercise). Print and discuss the results.
B7. Search the internet for (and print the best examples of) real-time weather-map analyses or forecasts (from numerical models) showing plotted fields of the four conditions needed for convective storm formation. (Hint, you might find these 4 conditions on 4 separate maps, so you should print and discuss all 4 maps.) Discuss.
B8. Search the internet for maps showing real-time thunderstorm and tornado watches. Print and discuss the results. If you also did the previous exercise, then discuss the amount of agreement of the watch areas with the regions that satisfy the conditions for thunderstorms.
B9. Use the internet to find thunderstorm tutorials. (Hints: some elementary tutorials are at the “university of Illinois online meteorology guide” site. More advanced tutorials are at the “ucar meted” site. Much miscellaneous info is at the “Wikipedia” site.) After reading the tutorial, print and discuss one new aspect of thunderstorms that wasn’t in this textbook, but which you find interesting and/or important.
B10. Search the web for newer thunderstorm indices than were discussed in this chapter. Summarize and print key information (e.g., definitions for, equations governing, advantages compared to older indices) for one of these new indices, and if possible show a real-time map of the values of this index.
B11. Search the internet for a recent sounding close to your present location. Get and print this sounding data in text form. Then manually plot the temperatures and dew points on a thermo diagram, and plot the winds on a hodograph. Manually calculate a few key thunderstorm indices, and make your own forecast about whether thunderstorms are likely.
B12. Same as the previous exercise, but for a sounding just ahead of a severe thunderstorm location.
B13. Search the internet for a “storm spotter glossary”, and list 10 new thunderstorm-related terms and their definitions that were not discussed in this chapter, but which you feel are important. Justify your choice of terms.
B14. Search the internet for (& print good examples of) new research that is being done on thunderstorms or any of the topics discussed in this chapter.
B15. Search the internet for four key storm components that spotters analyze to estimate thunderstorm strength, type, and stage of evolution.
B16. Search the internet to explain the difference between “storm chasers” and “storm spotters”.
B17. Search the internet to find which agency or agencies within your own country are responsible for making the national forecasts of severe thunderstorms. Print their web address, along with basic information about their mission and location. Also, find and print a list of qualifications they want in new meteorologists that they hire.
B18. For the following country, where on the internet can you find up-to-date tornado/thunderstorm watches/warnings?
| a. Canada | b. Japan | c. China |
| d. Australia | e. Europe | f. USA |
| g. or a teacher-assigned country? | ||
14.10.2. Apply
A1(§). Plot the pressure difference (∆P = PMCS – Pstd. atm.) vs. height within a mesoscale convective system (MCS), given the temperature differences (∆T = TMCS – Tstd.atm.) below. Also plot the given temperature difference vs. height. The surface pressure PMCS sfc under the MCS is also given below. For the standard atmosphere (std. atm.), assume the surface pressure is 101.325 kPa. Use a vertical resolution of ∆z = 250 m.
| Exercise Part | a. | b. | c. | d. |
|---|---|---|---|---|
| ∆T (K) | ||||
| 0 ≤ z < 2 (km) | –10 | –8 | –13 | –15 |
| 2 ≤ z < 4 (km) | 0 | 0 | 0 | 0 |
| 4 ≤ z < 9 (km) | +6.5 | +5 | +10 | +9 |
| 9 ≤ z < 11 (km) | –10 | –7.7 | –15 | –13 |
| 11 ≤ z ≤ 12 (km) | 0 | 0 | 0 | 0 |
| PMCS sfc (kPa) | 101.8 | 101.7 | 101.9 | 102.05 |
A2. Using your answer for ∆P at 2 km altitude from the previous exercise, calculate the rear-inflow jet (RIJ) speed into the mid-tropospheric meso-low within an MCS. Assume the RIJ is geostrophic, for a latitude of 40°N. Assume the MCS has a horizontal radius (km) of:
| a. 80 | b. 100 | c. 120 | d. 140 | e. 160 |
| f. 180 | g. 200 | h. 220 | i. 240 | j. 260 |
A3. Given the following prestorm sounding. Plot it on a thermo diagram (use a skew-T, unless your instructor specifies a different one). Find the mixedlayer height, tropopause height, lifting condensation level, level of free convection, and equilibrium level, for an air parcel rising from the surface. Use a surface (P = 100 kPa) dew-point temperature (°C) of:
| a. 22 | b. 21 | c. 20 | d. 19 | e. 18 | f. 17 | g. 16 |
| h. 15 | i. 14 | j. 13 | k. 12 | l. 11 | m. 10 | n. 9 |
| o. 8 | p. 7 | q. 6 | r. 5 | s. 4 |
Sounding:
| P (kPa) | T (°C) |
| 20 | –45 |
| 25 | –45 |
| 30 | –40 |
| 40 | –30 |
| 50 | –19 |
| 70 | +5 |
| 80 | 15 |
| 88 | 21 |
| 92 | 21 |
| 98 | 26 |
| 100 | 30 |
A4. Using the result from the previous exercise, forecast the intensity (i.e., category) of thunderstorm and possibly tornadoes that are likely, given the lifting condensation level you found.
A5. Find the median and interquartile range for the following data sets:
| a. | 6 | 3 | 9 | 7 | 2 | 1 | 6 | 0 | 8 | |||||
| b. | 8 | 5 | 9 | 8 | 1 | 1 | 3 | 2 | 6 | 8 | 4 | 9 | 7 | 0 |
| c. | 3 | 5 | 2 | 7 | 9 | 4 | 7 | 7 | ||||||
| d. | 9 | 6 | 8 | 0 | 9 | 1 | 3 | 2 | 9 | 7 | 8 | |||
| e. | 5 | 8 | 2 | 2 | 1 | 6 | 4 | 3 | 7 | 9 | ||||
| f. | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | ||||
| g. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
| h. | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | |||||
| i. | 0 | 0 | 0 | 0 | 3 | 6 | 8 | 3 | 4 | 8 | 9 | 0 | 6 |
A6. Find the mean and standard deviation for the data set from the previous exercise.
A7. For the sounding from exercise A3, find the value of surface-based CAPE, using:
(1) the height (z) tiling method.
(2) the pressure (P) tiling method.
Assume Tv ≈ T. Also, on the plotted sounding, shade or color the CAPE area.
A8. Start with the sounding from exercise A3. Assume that the forecast high temperature for the day is 2°C warmer than the surface temperature from the sounding. Find the value of surface-based CAPE. Assume Tv ≈ T.
A9. For the sounding from exercise A3, find the value of mean-layer CAPE. Assume Tv ≈ T. For the air parcel that you conceptually lift, assume its initial temperature equals the average temperature in the bottom 1 km of the sounding, and its initial dewpoint is the average dew-point temperature in the bottom 1 km of the sounding (assuming that the mixing ratio is constant with height in this 1 km mixed layer).
A10. Using the result from the previous exercise, forecast the intensity of thunderstorms and possibly tornadoes that are likely, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast, given the MLCAPE you found.
A11. Forecast the thunderstorm and/or tornado intensity, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast, given a ML CAPE (J·kg–1) value of:
| a. 1000 | b. 1250 | c. 1500 | d. 1750 | e. 2000 |
| f. 2250 | g. 2500 | h. 2750 | i. 3000 | j. 3250 |
| k. 3500 | l. 250 | m. 500 | n. 750 |
A12. Given the sounding from exercise A3, except with a surface temperature of T = 24°C at P = 100 kPa. Assume the surface dew point from exercise A3 defines a mixing ratio that is uniform in the bottom 2 layers of the sounding.
Find the most unstable CAPE considering air parcels that start their rise from just the bottom two levels of the sounding (i.e., for air parcels that start at P = 100 and 98 kPa). Assume Tv ≈ T.
A13. Using the result from the previous exercise, forecast the intensity (i.e., category) of thunderstorm and possibly tornadoes that are likely, given the MUCAPE you found, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast.
A14. Forecast the thunderstorm and/or tornado intensity, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast, given a MU CAPE (J·kg–1) value of:
| a. 1000 | b. 1250 | c. 1500 | d. 1750 | e. 2000 |
| f. 2250 | g. 2500 | h. 2750 | i. 3000 | j. 3250 |
| k. 3500 | l. 3750 | m. 4000 | n. 4250 | n. 4500 |
A15. Using the SBCAPE you found in exercise A7, and the sounding and key altitudes from exercise A3, find the value of normalized CAPE, indicate of the CAPE is tall thin or short wide, and suggest whether thunderstorms would favor heavy precipitation or tornadoes.
A16. Estimate the max likely updraft speed in a thunderstorm, given a SB CAPE (J·kg–1) value of:
| a. 1000 | b. 1250 | c. 1500 | d. 1750 | e. 2000 |
| f. 2250 | g. 2500 | h. 2750 | i. 3000 | j. 3250 |
| k. 3500 | l. 3750 | m. 4000 | n. 500 | n. 750 |
A17. Given a wind of (U, V) = (10, 5) m s–1 at z = 1 km. Find the wind difference magnitude, shear direction, and shear magnitude between z = 1 and 2 km, given winds at 2 km of (U, V) (m s–1) of:
| a. (20, –3) | b. (25, –15) | c. (30, 0) | d. (25, 5) |
| e. (10, 15) | f. (5, 20) | g. (–15, 15) | h. (–5, 0) |
| i. (–20, –30) | j. (–5, 8) | k. (–10, –10) | l. (0, 0) |
A18. Plot the following wind sounding data on a hodograph. (Make copies of the blank hodograph from Fig. 14.51 to use for all the hodograph exercises.)
| z (km) | In each cell: wind direction (°), speed (m s–1) | |||
|---|---|---|---|---|
| Exercise | ||||
| a | b | c | d | |
| 0 | calm | 100, 5 | 120, 8 | 150, 10 |
| 1 | 120, 5 | 120, 10 | 150, 5 | 180, 5 |
| 2 | 150, 8 | 160, 15 | 210, 5 | 240, 5 |
| 3 | 180, 12 | 220, 25 | 240, 10 | 260, 10 |
| 4 | 210, 15 | 240, 30 | 250, 15 | 260, 20 |
| 5 | 240, 25 | 250, 33 | 258, 25 | 250, 30 |
| 6 | 260, 40 | 250, 33 | 260, 35 | 240, 40 |
A19. On your plotted hodograph from the previous exercise, draw wind vectors from the origin to each wind data point. Discuss the relationship between these wind vectors and the original hodograph that connected just the tips of all the vectors.
A20. Using your hodograph plot from exercise A18, use the hodograph (not equations) to find the (U, V) components (m s–1) at each altitude in the sounding.
A21. Graphically, using your hodograph plot from exercise A18, plot the local shear vector (m s–1) across the z = 2 to 3 km layer.
A22. Same as the previous exercise, except solve for the local shear vector (m s–1) mathematically.
A23. Graphically, using your hodograph plot from exercise A18, plot the 0 to 6 km mean shear vector (m s–1).
A24. Same as exercise A23, except solve for the 0 to 6 km mean shear vector (m s–1) mathematically.
A25. Using your hodograph plot from exercise A18, graphically find the 0 to 6 km total shear magnitude (m s–1). Also, predict the likely thunderstorm and possibly tornado intensity based on this parameter, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast.
A26(§). Same as the previous exercise, except solve for the 0 to 6 km total shear magnitude (m s–1) mathematically. Also, predict the likely thunderstorm and possibly tornado intensity based on this parameter, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast.
A27. Predict the thunderstorm and possibly tornado intensity based on the following total shear magnitude (m s–1) across the 0 to 6 km layer, and indicate the uncertainty (i.e., the range of possible storm intensities) in this forecast.
| a. 4 | b. 6 | c. 8 | d. 10 | e. 12 | f. 14 | g. 16 |
| h. 18 | i. 20 | j. 22 | k. 24 | l. 26 | m. 28 | n. 30 |
A28. Graphically, using your hodograph plot from exercise A18, find the mean environmental wind direction (°) and speed (m s–1), for normal storm motion.
A29(§). Same as the previous exercise, except solve mathematically for the mean environmental wind direction (°) and speed (m s–1), for normal storm motion.
A30. Given the hodograph shape from exercise A18, indicate whether right or left-moving supercells would dominate. Also, starting with the “normal storm motion” from exercise A28 (based on hodograph from exercise A18), use the Internal Dynamics method on your hodograph to graphically estimate the movement (i.e., direction and speed) of
(1) Right-moving supercell thunderstorms
(2) Left-moving supercell thunderstorms
A31. Using your result from exercise A28 for normal storm motion (based on exercise A18), and assuming CAPE = 2750 J·kg–1:
(1) calculate the shear ∆M (m s–1) between the mean (0-6 km) environment winds and the average winds at z = 0.5 km.
(2) calculate the bulk Richardson number shear (BRN shear) in m2·s–2.
(3) calculate the bulk Richardson number (BRN).
(4) forecast the thunderstorm likelihood, thunderstorm type, and tornado intensity.
A32. Given the following value of bulk Richardson number, determine the likely thunderstorm type:
| a. 7 | b. 12 | c. 17 | d. 22 | e. 27 | f. 32 | g. 37 |
| h. 42 | i. 47 | j. 52 | k. 57 | l. 62 | m. 67 | n. 72 |
A33. Given the following value of bulk Richardson number (BRN) shear (m2·s–2), determine the likely thunderstorm and tornado intensity:
| a. 5 | b. 10 | c. 20 | d. 30 | e. 40 | f. 45 | g. 50 |
| h. 55 | i. 60 | j. 65 | k. 70 | l. 75 | m. 80 | n. 90 |
A34. Given the sounding from exercise A3, calculate the value of the convective inhibition (CIN) in J·kg–1 for an air parcel lifted from the surface. Assume Tv ≈ T. Also, shade or color the CIN area on the plotted sounding.
A35. Given your answer to the previous exercise, interpret the strength of the cap and how it affects thunderstorm triggering.
A36. Calculate the mean-layer CIN using the sounding from exercise A3. Temperatures in the bottom 10 kPa of atmosphere are as plotted from the sounding, and assume that the mixing ratio is constant over this layer and equal to the mixing ratio that corresponds to the surface dew point.
A37. For the sounding from exercise A3:
(1) To what altitude must a surface air parcel be lifted by an airmass boundary or a mountain, to trigger thunderstorms?
(2) To what temperature must the surface air be heated in order to convectively trigger thunderstorms (i.e., find the convective temperature), and what is the value of the convective condensation level?
A38. What values of K index, Lifted Index, Showalter Stability Index, SWEAT Index, and Total-totals Index would you anticipate for the following intensity of thunderstorm (CB)?
- no CB
- ordinary CB
- marginal supercell
- supercell with no tornado
- supercell with EF0 - EF1 tornado
- supercell with EF2 - EF5 tornado
A39. What value of the Bulk Richardson Number, BRN-Shear, ML CAPE, MU CAPE, CIN, Energy Helicity Index, Lifting Condensation Level, Supercell Composite Parameter, 0-6 km Shear, Storm-Relative Helicity, effective Storm-Relative Helicity, and Significant Tornado Parameter would you anticipate for the following intensity of thunderstorm (CB)?
- no CB
- ordinary CB
- marginal supercell
- supercell with no tornado
- supercell with EF0 - EF1 tornado
- supercell with EF2 - EF5 tornado
14.10.3. Evaluate & Analyze
E1. Identify as many thunderstorm features as you can, from the photo below. (Image “wea00106” courtesy of NOAA photo library).

E2. Why does a thunderstorm have a flat (anvil or mushroom) top, instead of a rounded top such as cumulus congestus clouds? (Ignore the overshooting dome for this question.
E3. Almost all clouds associated with thunderstorms are caused by the lifting of air. List each of these clouds, and give their lifting mechanisms.
E4. Consider Figs. 14.4a & b. If you were a storm chaser, and were off to the side of the storm as indicated below, sketch which components of the storm and associated clouds would be visible (i.e., could be seen if you had taken a photo). Label the key cloud features in your sketch. Assume you are in the following direction from the storm:
| a. northeast | b. southwest | c. northwest |
For example, Fig. 14.4a shows the sketch for the view from southeast of the storm.
E5. Consider Fig. 14.4b. If a Doppler radar were located near the words in that figure given below, then sketch the resulting color patterns on the Doppler PPI wind display for near-surface winds.
| a. “FFD” | b. “RFD” | c. “Anvil Edge” | d. “Cu con” | e. “Gust Front” | f. “Beaver Tail” |
| g. “Outflow Boundary Layer Winds” | h. “Inflow Boundary Layer Winds” | i. “Main Updraft” | j. “Storm Movement” | k. “Forward Flank Downdraft” | |
E6. Circle the stations in the weather map below that are reporting thunderstorms. (Image courtesy of the Storm Prediction Center, NWS, NOAA.
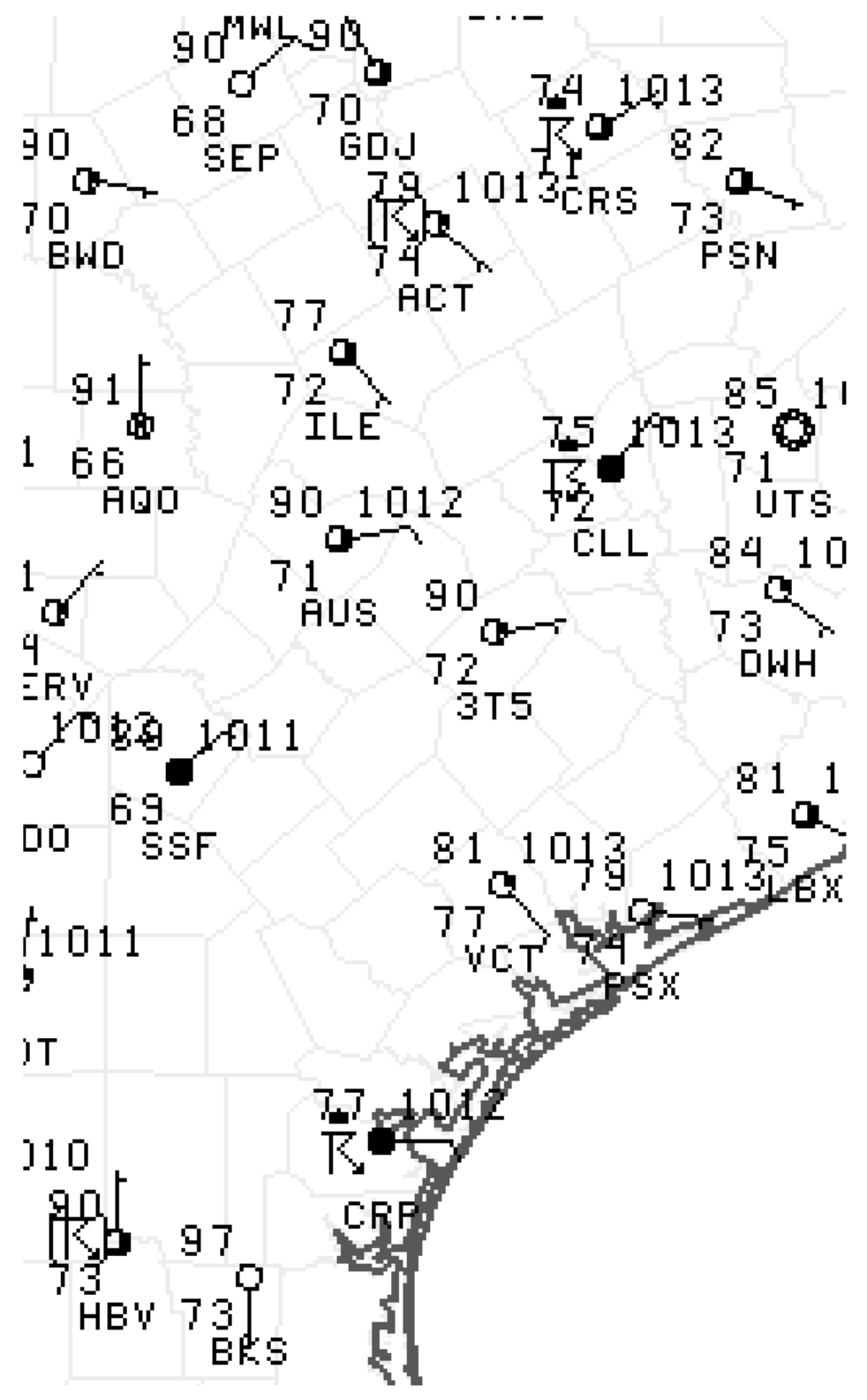
E7. Can a thunderstorm exist without one or more cells? Explain.
E8. For each thunderstorm type or organization, explain which triggered mechanism(s) would have most likely initiated it.
E9. For each thunderstorm type or organization, explain how the phenomenon would differ if there had been no wind shear.
E10. What is a derecho, and what causes it? Also, if strong straight-line winds can cause damage similar to that from a weak tornado, what are all the ways that you could use to determine (after the fact) if a damaged building was caused by a tornado or derecho?
E11. Summarize the different types of supercells, and list their characteristics and differences. Explain what factors cause a supercell to be of a specific type, and where you would most likely find it.
E12. In a thunderstorm, there is often one or more updrafts interspersed with one or more downdrafts. Namely, up- and down-drafts are often adjacent. Do these adjacent up- and down-drafts interfere or support each other? Explain.
E13. List the 4 conditions needed for thunderstorm formation. Then, consider a case where one of the conditions is missing, and explain why thunderstorms would be unlikely, and what would form instead (if anything). Do this for each of the 4 conditions separately.
E14. If thunderstorms normally occur at your town, explain how the 4 conditions needed for thunderstorm formation are satisfied for your region. Namely, where does the humid air usually come from, what conditions contribute to shear, what trigger mechanisms dominate in your region, etc.
E15. If thunderstorms are rare in your region, identify which one or more of the 4 conditions for thunderstorms is NOT satisfied, and also discuss how the other conditions are satisfied for your region.
E16. If the cap inhibits thermals from rising, why is it considered a good thing for thunderstorms?
E17. If your national weather service were to make only one upper-air (rawinsonde) sounding per day, when would you want it to happen, in order to be most useful for your thunderstorm forecasts?
E18. In the section on convective conditions and key altitudes, one thermo diagram was presented with the LCL above zi (the mixed layer top), while the Sample Application showed a different situation with the LCL below zi . Both are frequently observed, and both can be associated with thunderstorms.
Discuss and justify whether it is possible to have an environment favorable for thunderstorms if:
- zi is above the LFC
- zi is above the tropopause
- LCL is at the Earth’s surface
- LFC is at the Earth’s surface
- LCL is above the LFC
E19. The tops of thunderstorms are often near the tropopause.
- Why is that?
- Why are thunderstorm tops usually NOT exactly at the tropopause.
E20. Based on tropopause info from earlier chapters, how would you expect thunderstorm depth to vary with:
- latitude
- season
E23. Same as the previous exercise, but for the sounding given in the Sample Application after Fig. 14.26.
E24. Fig. 14.22 shows schematically the information that is in Fig. 14.25. Explain how these two figures relate to each other.
E25. Consider Fig. 14.22. Why is the following environmental condition conducive to severe thunderstorms?
- cold air near the top of the troposphere
- dry air near the middle of the troposphere
- a stable cap at the top of the boundary layer
- a warm humid boundary layer
- wind shear
- strong winds aloft.
(Hint, consider info from the whole chapter, not just the section on convective conditions.)
E26. Fig. 14.26 shows a nonlocally conditionally unstable environment up to the EL, yet the sounding in the top of that region (i.e., between the tropopause and the EL) is locally statically stable. Explain how that region can be both stable and unstable at the same time.
E27. How much energy does an airmass thunderstorm release (express your answer in units of megatons of TNT equivalent)? Assume all the water vapor condenses. Approximate the cloud by a cylinder of radius 5 km, with base at P = 90 kPa and top at P = 30 kPa. The ABL air has depth 1 km, and dew-point temperature (°C) of:
| a. 17 | b. 16 | c. 15 | d. 14 | e. 13 | f. 12 | g. 11 |
| h. 18 | i. 19 | j. 20 | k. 22 | l. 23 | m. 24 | n. 25 |
E28. Why do thunderstorms have (nearly) flat bases? (Hint, what determines the height of cloud base in a convective cloud?)
E29. Compare the different ways to present information about “high humidity in the boundary layer”, such as the different weather maps shown in that section. What are the advantages and disadvantages of each?
Normally, meteorologists need use only one of the humidity metrics to get the info they need on moisture availability. Which one moisture variable would you recommend using, and why?
E30. Look up the definitions of the residual layer and nocturnal stable layer from the Atmospheric Boundary Layer chapter. Consider atmospheric conditions (temperature, humidity) in the residual layer, relative to the conditions in the mixed layer from the afternoon before. Use this information to explain why strong thunderstorms are possible at night, even after the near-surface air temperature has cooled significantly
E31. Often statistical data is presented on a boxand-whisker diagram, such as sketched below.
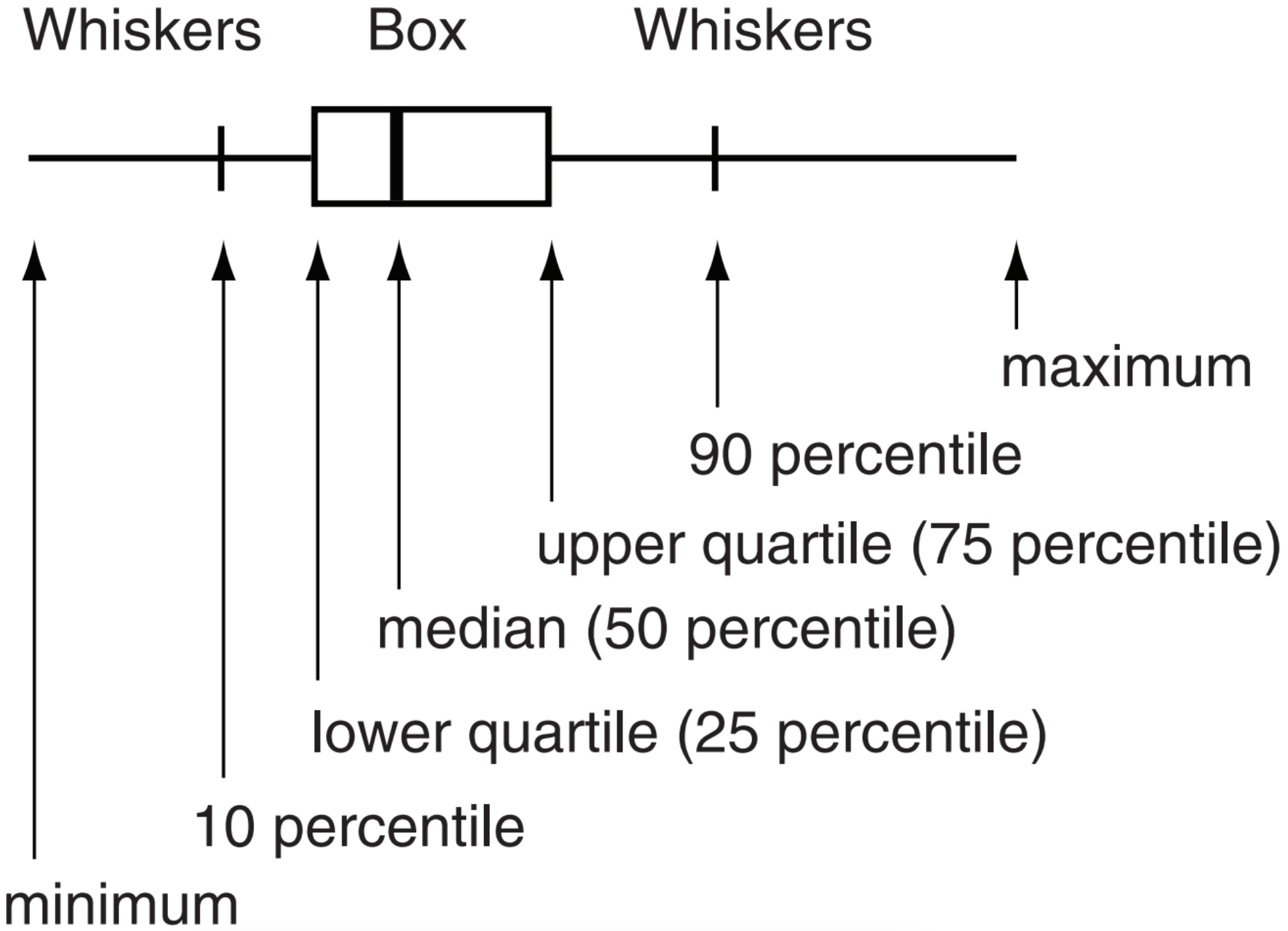
For example, the data such as in Fig. 14.33 is often presented in the journal literature as shown below (where the max and min values are not shown for this illustration, but are often given in the literature).
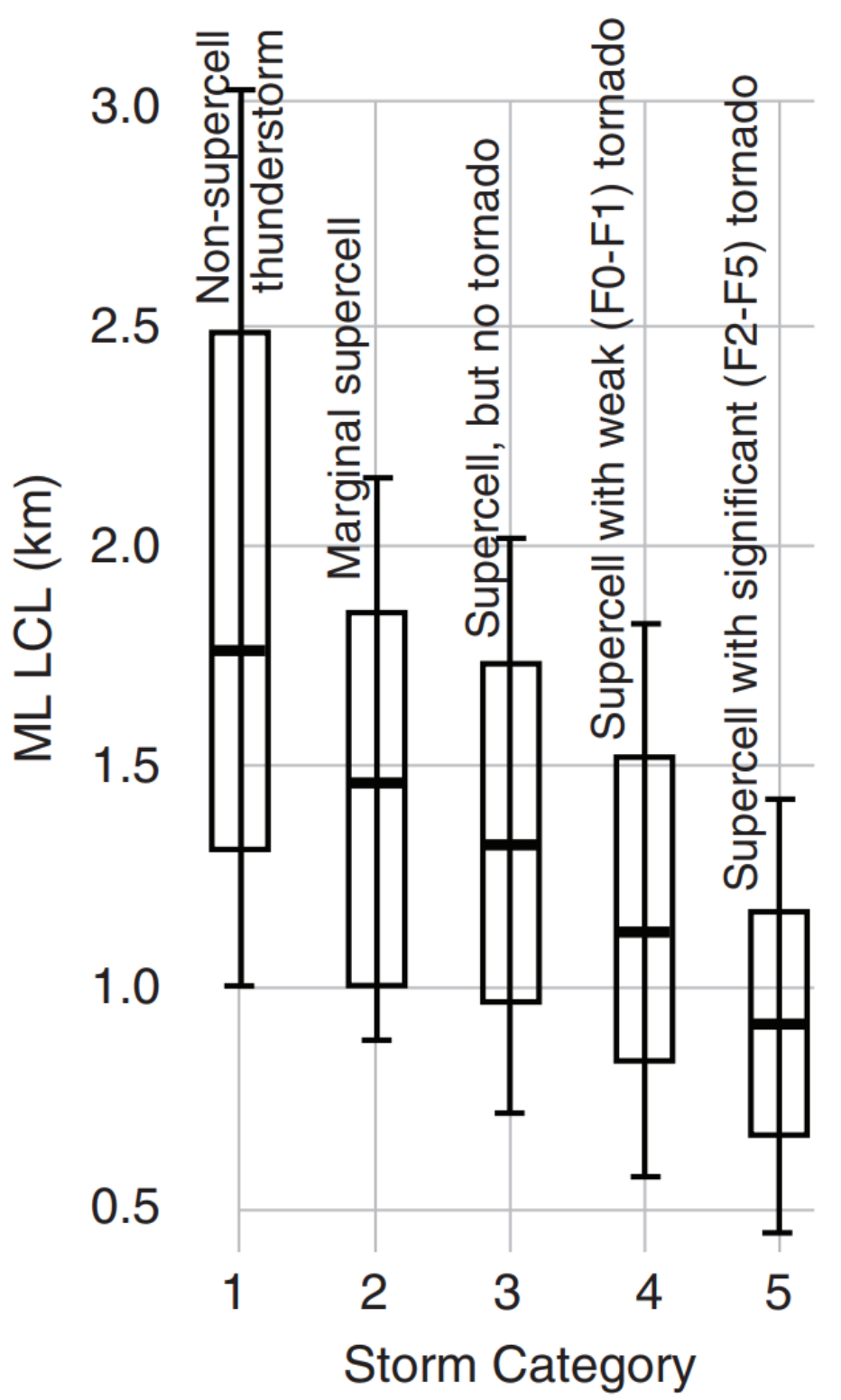
Create box-and-whisker diagrams, using data in this textbook for:
- ML CAPE
- MU CAPE
- TSM
- BRN Shear
- 0-1 km SRH
- 0-1 km EHI
E32. Look at a blank thermo diagram. At colder temperatures, the moist adiabats don’t deviate far from the dry adiabats. Use this characteristic to help explain why CAPE is smaller for colder environments, and thus why strong thunderstorms are less likely.
E33. Thunderstorms are much more prevalent in the tropics than near the poles. Use all the info from this chapter to help explain this. Also relate it to info in other chapters, such as: radiation, global circulation, boundary layers etc.
E34. If you were given a file of ASCII text data of temperature and dew point vs. height in a sounding, show schematically (i.e., with a flow chart) a computer program that you could write to compute the CAPE. Don’t actually write the program, just show the main steps, procedures, and/or data structures that you would use. (Hint: the method in Fig. 14.35 might be easier than the method in Fig. 14.36, especially for very small ∆z.)
a. Do this based on eq. (14.2) [gives an approximate answer]
b. Do this based on eq. (14.1) [this is more accurate]
E35. Describe all the factors in a plotted sounding that could contribute to larger CAPE values.
E36. Compare and contrast the different parcel-origin methods for computing CAPE (SB, forecast SB, ML, and MU). Recommend which methods would be best for different situations.
E37. Derive eq. (14.5) from eq. (14.4) by using the hypsometric equation. Show your steps.
E38. Critically analyze eq. (14.6). Discuss the behavior of the equation as the height difference between the LFC and EL approaches zero.
E39. Consider CAPE in a prestorm sounding.
- Can all the CAPE be consumed by the storm?
- Do the CAPE eqs. have limitations? Discuss.
- Are there reasons why thunderstorm vertical velocity might not get as large as given in eq. (14.8)?
E40. a. Is wind shear a vector or scalar quantity? Why?
b. Is it possible to have non-zero shear between two altitudes where the winds have the same speed? Explain.
E41. Suppose that Fig. 14.47 gives the winds relative to the ground. Redraw that figure showing the storm-relative winds instead. Also, explain why storm-relative winds are important for thunderstorm dynamics.
E42. On a hodograph, why is it important to list the altitude of the winds next to each wind data point?
E43. Draw a hodograph showing an environment where winds ____ with height. a. veer b. back
E44. On blank hodographs such as Fig. 14.51, why are the printed wind directions 180° out of phase with the normal compass directions?
E45. In Fig. 14.52, notice that the dark vertical and horizontal lines don’t look straight. This is an optical illusion caused by the background circles of the hodograph. In fact, they are straight, as you can see by tilting the page so you are looking almost edgeon, sighting down each line. Based in this info, discuss why you should never draw the vertical or horizontal lines by eye, when trying to determine U and V components of wind.
E46. Three different types (i.e., ways of measuring) of shear vectors are shown in Fig. 14.53. Explain and contrast them.
E47. Create a table listing all the different types of shear that are discussed in this chapter, and add a column to the table that indicates what thunderstorm characteristics can be estimated from each shear type.
E48. A thunderstorm index or parameter is useful only if it can discriminate between different storm types or intensities. Using Fig. 14.56, critically evaluate the utility of TSM in estimating storm and tornado intensity.
E49. Explain the difference between the mean shear vector (as in Fig. 14.53) and the mean wind vector (as in Fig. 14.58), and discuss their significance.
E50. In Fig. 14.59, the mean wind is estimated as the center of mass of the shaded area. Is the actual mean wind exactly at the center of mass of the shaded area, or only close? [Hint, to help think about this question, create some very simple hodographs with simple shapes for the shaded area [such as a rectangle] for which you can calculate the exact center of mass. Then see if you can extend your argument to more complex, or arbitrary shapes. This scientific approach is called inductive reasoning (see p107).]
E51. Using information from Fig. 14.61, identify where in Fig. 14.60 are the right and left moving mesocyclones.
E52. Although Fig. 14.62c shows a hodograph that is concave up, the whole curve is above the origin. Suppose that, on a different day, the hodograph has the same shape, but is shifted to be all below the origin. Assume N. Hemisphere, mid-latitudes.
Would such a hodograph still favor left-moving supercell storms? Justify your answer.
E53. Both the bulk Richardson number (BRN) and the Supercell Composite Parameter (SCP) include CAPE and shear. However, BRN is CAPE/shear, while SCP is CAPE·shear (times a third factor that we can ignore for this Exposition). Which (BRN or SCP) would you anticipate to give the best storm intensity forecasts, and which is most physically justified? Explain.
E54. Figs. 14.67 - 14.69 show 3 different ways to calculate CIN. Discuss the advantages and disadvantages of each, and for which conditions each method is most appropriate.
E55. Table 14-4 relates CIN to the difficulty in triggering thunderstorms. For the “strong” and “intense” cap categories, can you think of a trigger mechanism that would be powerful enough to trigger thunderstorms? Explain.
E56. Figs. 14.71 and 14.73 show how thunderstorms can be triggered by warm, humid air forced to rise over an obstacle (cold air, or a mountain). In both situations, sometimes after the thunderstorms are triggered and develop to maturity, environmental wind shear causes them to move away from the triggering location. After they have moved away, what is needed in order for the supercell thunderstorm to continue to exist (i.e., not to die immediately after moving away from the triggering area)? Do you think this is possible in real life, and if so, can you give an example?
E57. Consider Fig. 14.74. The Regional Winds chapter states that buoyancy (gravity) waves need statically stable air to exist without damping. But thunderstorms need nonlocally conditionally unstable air to exist. These seems contradictory. Explain how it might be possible.
E58. Fig. 14.75 shows a way to estimate Tneeded for convection, given T and Td from a sounding earlier in the day. Although this is an easy method, it has a major flaw. Critically discuss this method. (Hint: what was assumed in order to use this method?)
E59. Step back from the details of thunderstorms, and look at the big picture. After the thunderstorm has occurred, some precipitation has fallen out, and there has been net heating of the air. Explain how these two processes affect the overall stability and entropy (in the sense of randomness) in the troposphere.
E60. Re-draw Fig. 14.76, but for a winter case over mid-latitude land where nocturnal cooling is longer duration than daytime heating, and for which the total accumulated heating during the day (because the sun is lower in the sky) is less than the accumulated cooling at night. Use you resulting figure to discuss the likelihood of thunderstorms in winter.
E61. Recall from other chapters that the ocean has a much large heat capacity than land, and thus has less temperature change during day and night. Redraw Fig. 14.76 for a location at a tropical ocean, and discuss how the resulting figure relates to thunderstorm occurrence there.
E62. Some of the older stability indices in Table 14-6 are very similar in basis to some of the newer indices in Table 14-5, as described throughout this chapter. The main differences are often that the old indices consider meteorological conditions at just a few levels, whereas the newer indices integrate (sum) over many levels. Create a table matching as many old indices to as many new indices as possible.
E63. Based on what you learned so far, which subsets of indices from Table 14-7 would you prefer to utilize in your own storm forecasting efforts, to forecast:
- hail
- heavy rain
- lots of lightning
- tornadoes
- strong straight-line winds
- downbursts
Justify your choices.
14.10.4. Synthesize
S1. Suppose that thunderstorms were typically 30 km deep. How would the weather and general circulation differ, if at all?
S2. How would general circulation differ if no thunderstorms exist in the atmosphere?
S3. Draw a supercell diagram similar to Fig. 14.4b, but for mid-latitudes in the southern hemisphere.
S4. Why do thunderstorms have flat, anvil-shaped tops, while cumulus congestus do not? Both reach their equilibrium level.
S5. Suppose that N. Hemisphere mid-latitude thunderstorms exist in an environment that usually has the same lower-tropospheric geographic arrangement of heat and humidity relative to the storm as our real atmosphere, but for which the winds aloft are from the east. How would thunderstorms differ, if at all?
S6. Suppose that thunderstorms never move relative to the ground. Could long-lasting supercells form and exist? Explain.
S7. In multicell storms, new cells usually form on the south side of the storm complex, closest to the supply of warm humid boundary-layer air. What changes in the environment or the thunderstorm might allow new cells to form on the north side of the storm? Assume N. Hemisphere.
S8. If orographic thunderstorms need the mountain-triggered lifting to be initiated, why can the storms persist after being blown away from the mountain?
S9. If the Earth’s surface were smooth (i.e., no mountain ranges), then describe changes in the nature of thunderstorms. Could this alter the weather in your region? Explain.
S10. Suppose a 100 km diameter circular region of warm humid boundary layer air existed, surrounding by much colder air. If the cold air all around the circle started advancing toward the center of the circle and thunderstorms were triggered along this circular cold front, then describe the evolution of the thunderstorms.
S11. In Fig. 14.14 showing a vertical slice through a mesoscale convective system, the arrows show winds being drawn in toward low pressure in the mid troposphere, and other arrows blowing outward from high-pressure in the upper troposphere. Explain how this could happen, because normally we would expect winds to circulate around highs and lows due to Coriolis force, and not to converge or diverge (assuming no frictional drag because we are not in the boundary layer).
S12. Could a classic supercell change into a low-precipitation or a high-precipitation supercell? Explain what factors might cause this, and how the storm would evolve.
S13. If there was never a cap on the atmospheric boundary layer, explain how thunderstorms would differ from those in our real atmosphere, if at all.
S14. Start with the sounding in Fig. 14.24. Modify the dew point in the mid troposphere to create a new sounding that would support a layer of altocumulus castellanus (accus) clouds.
S15. Suppose that thunderstorm downdrafts could never penetrate downward through the cap at the top of the boundary layer. Explain how thunderstorms would differ, if at all?
S16. Suppose that shading of the ground by clouds would cause the Earth’s surface to get warmer, not cooler during daytime. How would thunderstorms and climate differ, if at all?
S17. Suppose the atmospheric sounding over your town showed conditions nearly, but not quite, favorable for the existence of thunderstorms. If you could cause the surface energy balance over land to be partitioned differently between sensible and latent heat, how would you partition it in order to generate a thunderstorm? Note that given a fixed input of energy from the sun, increasing either the temperature or the humidity would decrease the other variable.
S18. When water vapor condenses in thunderstorms, suppose that the air cools instead of warms. Would thunderstorms occur? If so, describe their behavior.
S19. In the Exposition of rising air parcels in a nonlocally conditionally unstable environment, we assumed that the surrounding environment was not changing. But if there are many air parcels rising in a thunderstorm updraft, then there must be compensating subsidence in the environment that advects downward the temperature and moisture layers. How would this alter our description of the evolution of thunderstorms?
S20. Under what conditions would the median of a distribution exactly equal the mean? Under what conditions would half the interquartile range exactly equal the standard deviation?
S21. Consider Fig. 14.34. Suppose that when the air parcel is above its LFC, that it entrains environmental air at such a high rate that the air parcel follows a thermodynamic path that is exactly half way between the environment and the moist adiabats that passes through it at each height during its rise. Sketch the resulting path on a copy of Fig. 14.34, and discuss how thunderstorms would differ, if at all.
S22. Consider Fig. 14.34. Suppose that there is no frictional drag affecting the rising air parcel. All of the CAPE would lead to kinetic energy of the updraft. Once the air parcel reaches its EL, inertia would cause it to continue to rise (i.e., overshoot) until its negative potential energy (by being colder than the environment) balanced the initial kinetic energy. Assuming an isothermal sounding above the tropopause in that figure, determine exactly how high the overshooting air parcel would rise. Also, discuss whether such behavior is likely in real thunderstorms.
S23. Suppose that no wind shear existed in the environment. How would thunderstorms differ, if at all?
S24. Suppose that the wind profile of Fig. 14.53 (based on the wind data tabulated in a Sample Application a couple pages earlier) corresponded to the same environment as the thermodynamic sounding data in Fig. 14.24. Draw “phase-space” plots as follows:
| a. T vs. U | b. T vs. V | c. T vs. M | d. Td vs. U |
| d. Td vs. U | e. Td vs. V | f. Td vs. M | g. T vs. Td |
(Hint: “phase-space” plots are explained in the Numerical Weather Prediction chapter as a way to help analyze the chaos of nonlinear-dynamics systems.)
Also, speculate on whether phase-diagram plots of real thunderstorm environments could be used to help forecast different types of thunderstorms.
S25. Suppose that moist adiabats curve concave upward instead of concave downward. How would thunderstorms be different, if at all?
S26. Suppose that the data plotted in the hodograph of Fig. 14.62b were everywhere below the origin of the hodograph. How would thunderstorms differ, if at all?
S27. Suppose that right-moving supercells altered the environment so that it favored left-moving supercells, and left-moving supercells altered the environment to favor right movers. How would thunderstorms differ, if at all?
S28. Suggest 3 or more thunderstorm trigger mechanisms beyond what was already discussed in this chapter.
S29. From the Precipitation chapter, recall the Wegener-Bergeron-Findeisen (WBF) cold-cloud process for forming precipitation. Describe the nature of thunderstorms if the WBF precipitation did not occur.
S30. Suppose that accurate thunderstorm (including hail, lightning, and tornado) warnings could be issued 2 days in advance. How would society and commerce change, if at all.


