5.0: Homework Exercises
- Page ID
- 9924
5.10.1. Broaden Knowledge & Comprehension
B1. Use the internet to acquire a map of rawinsonde sounding locations for your part of the world, and determine which four sounding locations are closest to your school.
B2. Use the internet to acquire WMO (World Meteorological Organization) and ICAO (International Civil Aviation Organization) identification codes for the four sounding locations closest to your school or business. For each of those four locations, what is the latitude, longitude, topographic elevation, and other info about the site.
B3. Use the internet to acquire different thermo diagrams (e.g., Emagrams, skew-Ts, Stüve diagrams, tephigrams, etc) for the most recent rawinsonde sounding made at the launch site closest to your school or business. Which web site (URL) has the diagram that is clearest or easiest to read?
B4. Use the internet to acquire today’s surface weather data of (P, T, and Td) for the a weather station that is near you. After plotting those on a skew-T diagram, use graphical methods to estimate the lifting condensation level. How does this height compare to any cumulus cloud bases that might be reported from the same station?
B5. Use the internet to acquire rawinsonde data in text form (i.e., a table of numbers) for an upper-air station near you, or a different station that your instructor assigns. Then plot this sounding by hand on a large thermo diagram (skew-T, unless your instructor indicates a different diagram). Determine the LCL for an air parcel rising from the surface.
B6. Use the internet to acquire a sequence of 4 successive soundings from a single rawinsonde station assigned by your instructor. Describe the evolution of the air at that location (e.g., warming, cooling, getting more humid, getting windier, etc.).
B7. Use the internet to acquire an already-plotted sounding near your location prior to a rain storm. From the plotted sounding, determine the temperature and mixing ratio near the ground, and then move that hypothetical air parcel upward to a pressure of 40 kPa. Use the thermo diagram to estimate the final liquid-water mixing ratio of the parcel. Can you relate the actual precipitation depth that was observed from this storm to your hypothetical liquid-water mixing ratio? Would you get a more-realistic answer if you stopped the parcel at a different pressure?
B8. In the Thunderstorm chapters you will learn additional ways to use soundings on thermo diagrams to help estimate thunderstorm strength, tornado likelihood, and other storm characteristics. As a preview of this application, find on the internet an already-plotted sounding that also shows wind information or Convective Available Potential Energy (CAPE) or other stability indices. See if that web site has a link to a legend that defines those terms. If so, use that legend to interpret the stability indices on the sounding, and explain what they mean.
B9. Use the internet to acquire a sounding for a nearby location (or other site that your instructor assigns) that you can output in both plotted graph and text form. Use the plotted sounding to determine the static stability at all heights, using the apex parcel method. Use the text data to calculate Brunt-Väisälä frequency and bulk Richardson number in the stable layers. Combine your dynamic and static stability info to suggest which regions in the sounding are turbulent. [Hints” (1) For any stable layer with uniform lapse rate within it, use only the temperatures and winds at the top and bottom of the layer to calculate these variables. (2) Ignore any moisture indicated by the sounding, and assume Tv ≈ T].
B10. Use the internet to acquire a plotted sounding from early in the morning. Suppose that as the day evolves, the near-surface dew-point temperature doesn’t change, but the near-surface air temperature becomes warmer. Considering nonlocal static stability effects, how warm would the near-surface air parcel need to become later that day in order for it to be positively buoyant (dry below the LCL, saturated above the LCL) up to a height where P = 60 kPa? Draw that air-parcel path on the sounding diagram, and discuss where cloud base and cloud top would be.
B11. Use the internet to acquire a plotted sounding near you. Estimate the pressures at the boundarylayer top and at the tropopause. Draw these locations on your thermo diagram, and discuss how you found them based on your sounding.
B12. Use the internet to acquire images of KelvinHelmholtz waves and billow clouds. Print two examples of each, along with their URLs.
5.10.2. Apply
A1. Identify the thermo diagram type.
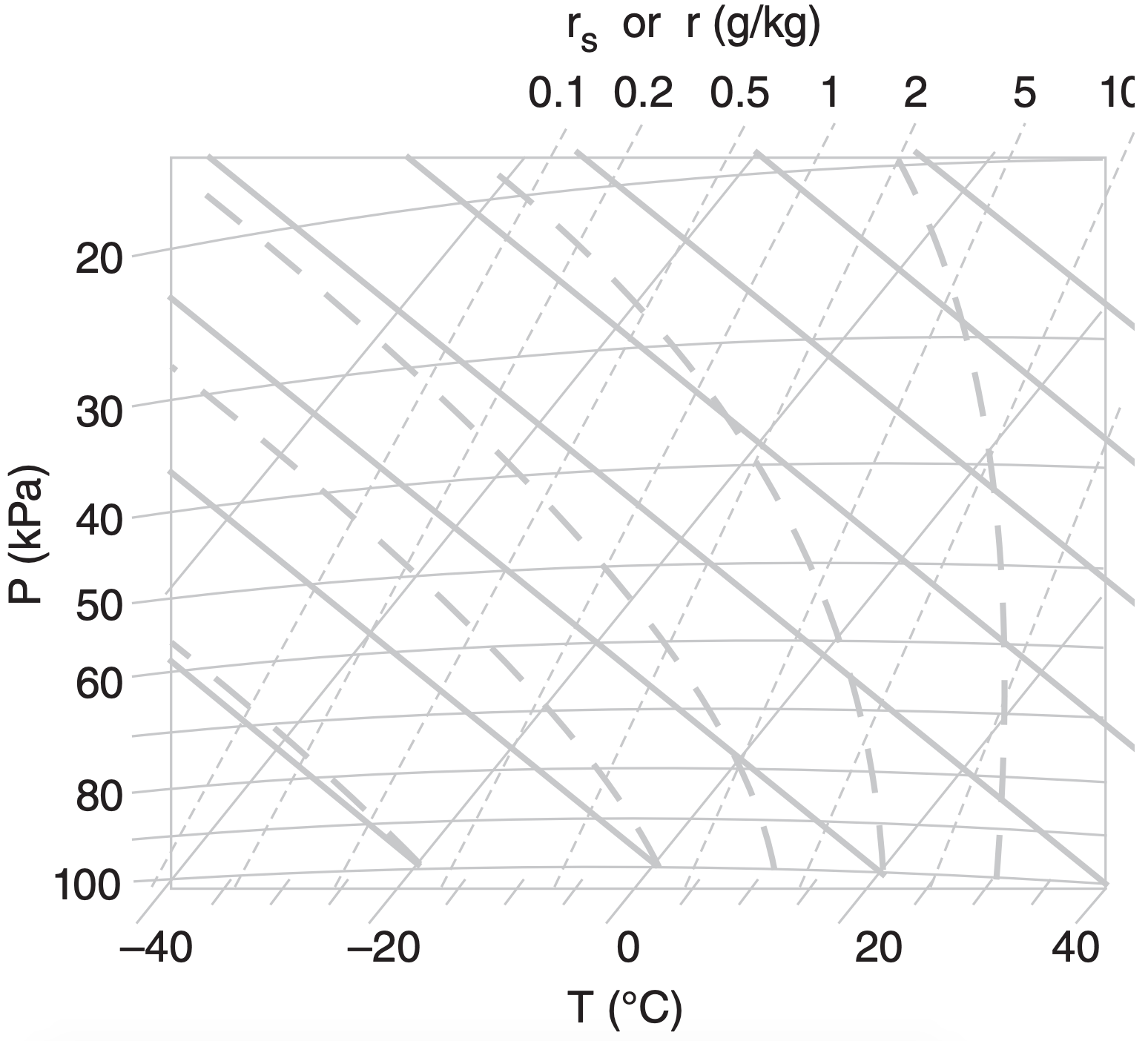
b)
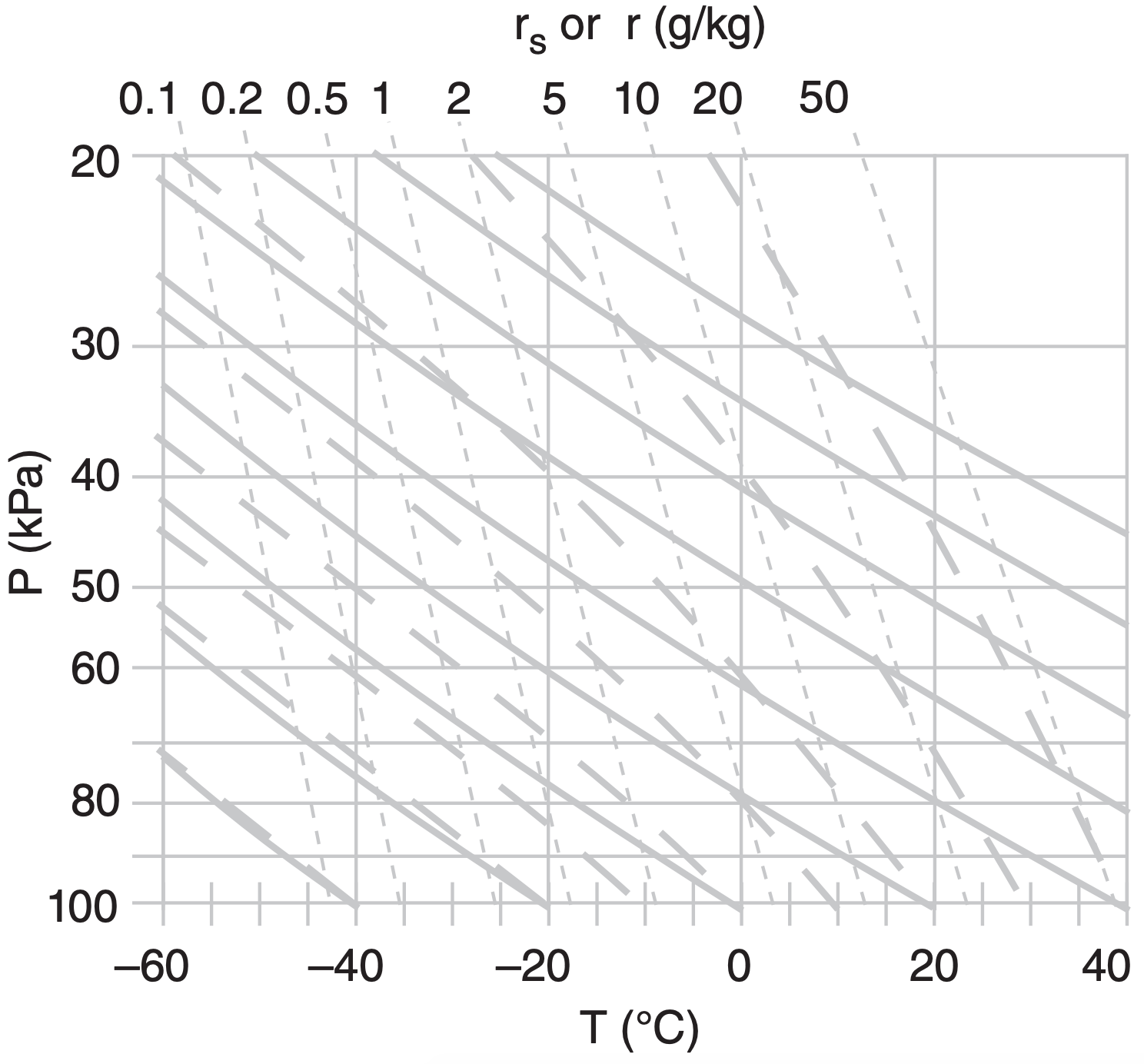
c)
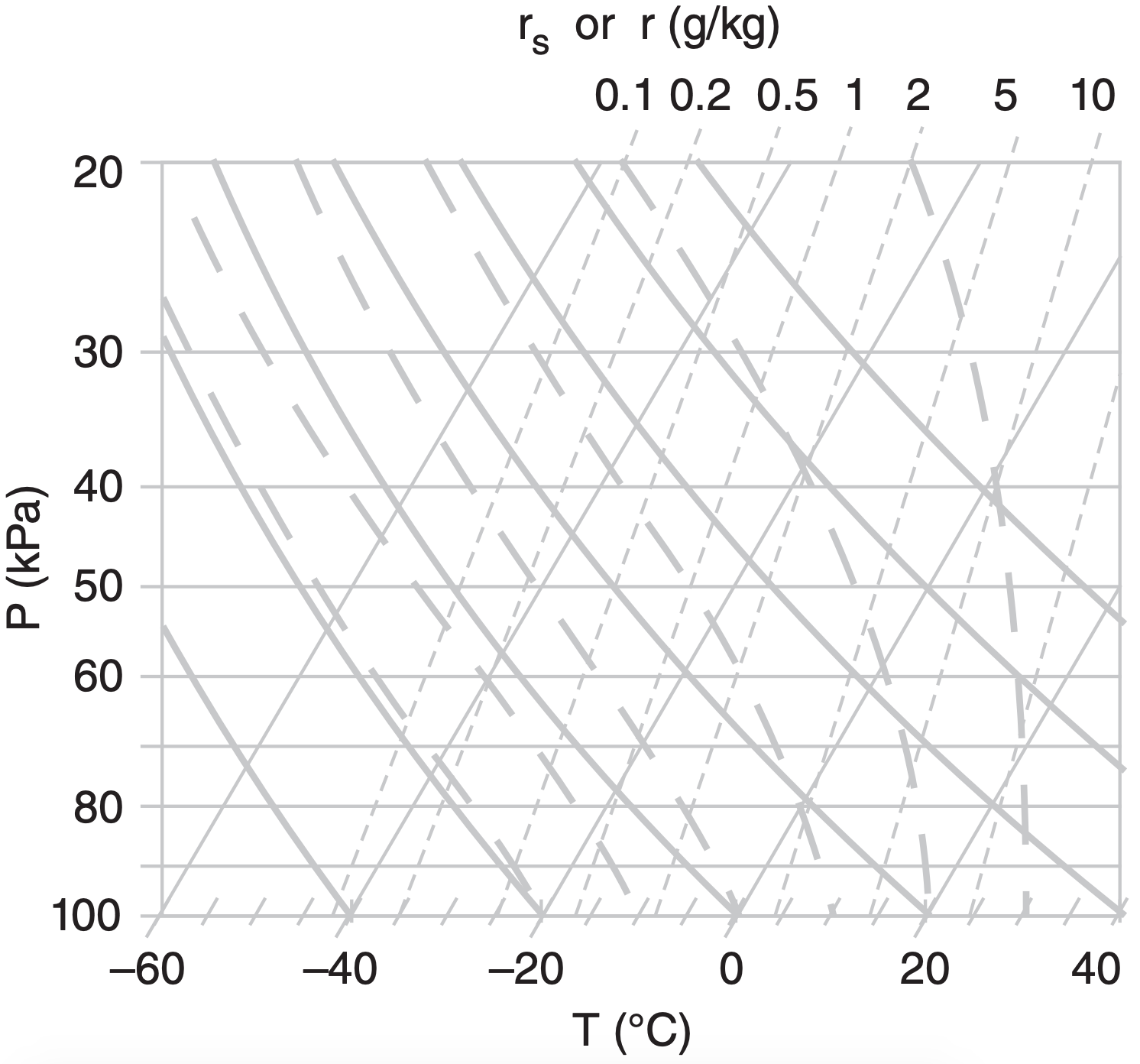
d)
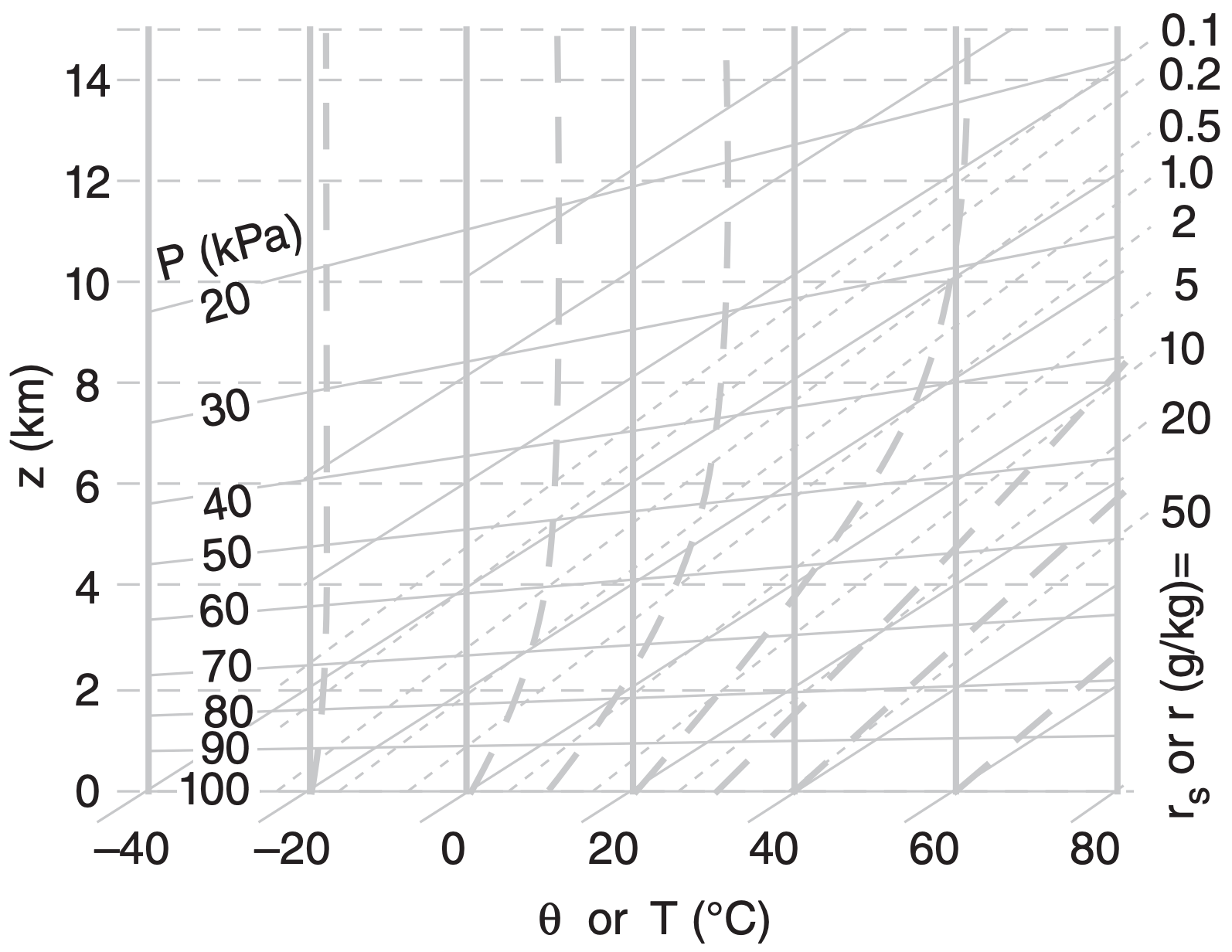
e)

A2. On copies of ALL 5 thermo diagrams from A1, find and label one of the:
| a. dry adiabats | b. isohumes |
| c. isobars | d. isentropes |
| e. saturated adiabats | f. isotherms |
| g. moist adiabats |
A3(§). Use a spreadsheet to create the Skew-T, as given in the Sample Application in the Skew-T section of this Chapter, except do it for isopleths listed below. Describe the results of your experiments with different values of the coefficient K, which determines the amount of skewness.
| T, θ, & θw (°C) | r (g kg–1) | |
| a. | 30 | 50 |
| b. | 25 | 20 |
| c. | 15 | 10 |
| d. | 10 | 2 |
| e. | 5 | 1 |
| f. | 0 | 0.5 |
| g. | –5 | 0.2 |
| h. | –10 | 0.1 |
| i. | –15 | 15 |
| j. | –20 | 25 |
A4. Make a copy of the page holding the thermo diagrams for exercise A1. Then, on all these diagrams, plot the one thermodynamic state given below. (Note: these are single air parcels, not components of a sounding.)
| P(kPa) | T(°C) | Td(°C) | |
| a. | 50 | 0 | –15 |
| b. | 80 | –5 | –10 |
| c. | 35 | –25 | –30 |
| d. | 75 | 25 | 16 |
| e. | 60 | 15 | –10 |
| f. | 90 | 20 | 10 |
| g. | 65 | –25 | –40 |
| h. | 85 | –10 | –30 |
| i. | 70 | 10 | 5 |
| j. | 80 | 15 | 10 |
| k. | 55 | –10 | –15 |
A5. Using thermodynamic state of the air parcel given in the previous exercise, plot it on the end-ofchapter large thermo diagram specified by your instructor (if none specified, use the skew-T diagram). Hint: Use a copy of a blank thermo diagram so you can keep the master copy clean.
A6. Plot the one thermodynamic state from exercise A4 on one large thermo diagram specified by your instructor (if none specified, use the skew-T). For that plotted point, use the thermo diagram (not equations) to find the values of the following items:
- mixing ratio
- potential temperature
- wet-bulb temperature
- wet-bulb potential temperature
- saturation mixing ratio
- LCL
- relative humidity
- equivalent potential temperature
A7. Same as A6, but use only an Emagram or Stüve.
A8. Starting with one assigned air-parcel with state from question A4:
- lower it to a pressure of 100 kPa, and find its new temperature and dew point. Use only a tephigram or Skew-T.
- lower it to a pressure of 100 kPa, and find its new temperature and dew point. Use only a Stüve or Emagram.
- raise it to a pressure of 20 kPa, and find its new temperature and dew point. Use only a tephigram or Skew-T.
- raise it to a pressure of 20 kPa, and find its new temperature and dew point. Use only a Stüve or Emagram.
A9. Which thermo diagrams from Figure 5.3 have
- straight isobars?
- straight dry adiabats?
- straight moist adiabats?
- have the greatest angle between isotherms and dry adiabats?
- moist adiabats that asymptotically approach dry adiabats near the top of the diagram?
- moist adiabats that asymptotically approach dry adiabats near the left of the diagram?
A10. Use the data below as an air-parcel initial state, and plot it on the specified large end-of-chapter thermo diagram. Assume this air parcel is then lifted to a final height where P = 25 kPa. Find the final values of the following variables Td, rs, T, rL, and rT.
| P(kPa) | T(°C) | Td(°C) | Thermo Diagram | |
| a. | 95 | 30 | 15 | Stüve |
| b. | 95 | 30 | 25 | Tephigram |
| c. | 95 | 20 | 10 | Skew-T |
| d. | 95 | 15 | –5 | Skew-T |
| e. | 100 | 25 | 10 | Emagram |
| f. | 100 | 25 | 5 | Tephigram |
| g. | 100 | 30 | 20 | Emagram |
| h. | 100 | 15 | 5 | Stüve |
| i. | 90 | 20 | 5 | Tephigram |
| j. | 90 | 15 | 5 | Emagram |
| k. | 90 | 5 | –5 | Skew-T |
| l. | 90 | 10 | 0 | Stüve |
A11. Using the same thermo diagram as specified in exercise A10, find the pressure at the LCL for an air parcel that started with the conditions as specified in that exercise.
A12. Starting with the FINAL state of the air parcel specified from exercise A10, allow all of the liquid water to rain out (except if the liquid water from the final state of A10 was greater than 1 g kg–1, then allow only 1 g kg–1 of liquid water to rain out). Then lower the air parcel back to its starting pressure, and determine its new temperature and new dewpoint. Use the specified thermo diagram from A10.
A13. Starting with the FINAL state of the air parcel specified from exercise A10, allow radiative cooling to change the air parcel temperature by ∆T = –8°C. Then lower the air parcel back to its starting pressure, and determine its new temperature and dew point. Use the specified thermo diagram from A10.
Sounding Data. The data here gives environmental conditions (i.e, the ambient sounding). Use this sounding for the questions that follow. Given V = 0.
| P(kPa) | T(°C) | Td(°C) | U (m s–1) |
| 20 | –25 | –55 | 45 |
| 30 | –25 | –50 | 50 |
| 40 | –20 | –20 | 44 |
| 45 | –15 | –15 | 40 |
| 50 | –10 | –24 | 30 |
| 70 | 12 | –20 | 30 |
| 80 | 19 | 3 | 20 |
| 90 | 21 | 15 | 7 |
| 99 | 29 | 17 | 7 |
| 100 | 33 | 20 | 2 |
Definitions: Significant levels are altitudes where the sounding has a bend or kink. In between significant levels you must draw straight lines.
Layers are the regions of air that are in between two neighboring levels.
A14. Using the end-of-chapter large thermo diagram specified below, plot the sounding data from the previous column on that diagram. For temperatures, use solid filled circles (red if available), and then connect those temperature-sounding points from bottom to top of the atmosphere with straight line segments. For dewpoints, use an open circles (blue perimeter if possible), and connect those points with dashed straight line segments.
| a. Emagram | b. Tephigram | c. Skew-T |
| d. θ-Z diagram | e. Stüve |
A15. a. For each pressure and temperature pair in the sounding data, calculate the corresponding potential temperature. Then plot a graph of potential temperature vs. pressure, using linear scales for both graph axes.
b. Use the result from (a) and the humidity information from the sounding data to find virtual potential temperature, and then plot it vs. pressure using linear scales for both axes.
A16. Given the sounding data. Suppose that you create an air parcel at the pressure-level (kPa) indicated below, where that parcel has the same initial thermodynamic state as the sounding at that pressure. Then move that parcel up through the environment to the next higher significant level (i.e., next lower pressure). What is the value of the buoyant force/mass acting on the parcel at its new level?
| a. 100 | b. 99 | c. 90 | d. 80 | e. 70 | f. 50 | g. 45 | h. 40 | i. 30 |
A17. Given the sounding data. Find NBV and PBV for an air parcel that starts in the middle of the layer indicated below, and for which its initial displacement and subsequent oscillation is contained within that one layer. Use the layer with a bottom pressurelevel (kPa) of:
| a. 90 | b. 80 | c. 70 | d. 50 | e. 45 | f. 40 | g. 30 |
A18. Using the sounding data such as plotted for exercise A14, using the apex parcel method to find static stability for the one environmental layer, where the bottom of that one layer is at P (kPa) =
| a. 100 | b. 98 | c. 87 | d. 80 | e. 70 | f. 60 | g. 40 |
For this exercise you may assume the air is dry. Also, the stability in any one layer could depend on nonlocal effects from other layers.
A19. Same as A18, but find the layer stability using the sounding data.
A20. Using the sounding data, calculate Richardson number, which you can then use to find a layer’s dynamic stability, for the layer that has a layer base at level P (kPa) =
| a. 100 | b. 98 | c. 87 | d. 80 | e. 70 | f. 60 | g. 40 |
A21. Indicate which portions of the sounding above are likely to be turbulent, and explain why.
A22. Using the sounding data:
- Does the sounding data indicate the presence of a mixed layer near the ground? What is its corresponding depth, zi ?
- Determine the height of the tropopause.
- Locate any layer (stratiform) clouds that might be present in the environment.
A23. With the sounding data:
- Compare the LCL pressure heights found using a thermo diagram vs. that found using the equations from the Water Vapor chapter, for an air parcel starting with the initial state as given by the sounding data at 100 kPa.
- On the same thermo diagram from part (a), at what pressure altitude does the air parcel from (a) stop rising (i.e., what is the pressure at cloud top)? At cloud top in the cloud, find the mixing ratios for water vapor and liquid water.
- Suppose that all the liquid water that you found in part (b) were to precipitate out, after which the air parcel descends back to a pressure altitude of 100 kPa. Compare the initial and final relative humidities of the air parcel (i.e., before rising from 100 kPa, and after returning to 100 kPa).
A24. At P = 100 kPa, z = 0 km, an air parcel has initial values of T = 30°C and Td = 0°C. Use each of the large thermo diagrams at the end of this chapter to find the LCL. How do these LCL values compare to the theoretical value from the equation in the Water Vapor chapter?
5.10.3. Evaluate & Analyze
E1. If an unsaturated air parcel rises, why does its humidity follow an isohume (constant r) instead of an isodrosotherm (constant Td)?
E2. Suppose a rising dry air parcel cools at a rate different than Γd. What process(es) could cause this difference? Why?
E3. From the hypsometric equation one expects that colder air has thinner thickness. So why do the height contour lines on the large Emagram tilt down to the right, rather than down to the left?
E4. The large thermo diagrams at the end of the chapter have mixing-ratio labels near the top. Why don’t these label values increase linearly?
E5. Dry adiabats are perfectly straight lines on the Stüve diagram, but have slight curvature on the Emagram (see the large diagrams at the end of the chapter). If the dry adiabatic lapse rate is constant, why are the lines curved in the Emagram?
E6. On a thermo diagram, why are three points needed to represent any single air parcel?
E7. Could you determine the complete thermodynamic state of an air parcel given only its LCL and its initial (P, T)? Explain.
E8. The “air parcel” method of static stability assumes that the ambient environment doesn’t change as an air parcel moves through it. Under what conditions is this assumption good? When would the assumption fail?
E9. Given an air parcel of virtual temperature Tv, embedded in a uniform environment of the same Tv. Why does it have zero buoyant force, even though gravity is trying to pull the air parcel down?
E10. Can stationary metal vehicles float in air analogous to how metal ships can float on the ocean? If so, how should the metal aircraft be designed?
E11. Recall equations (5.2 & 5.3a) for buoyant force, based on difference between the air parcel (object) and its environment (surrounding fluid). Why does the equation using density difference have a different sign than the equation using virtual temperature?
E12. Compare the slope of the saturated adiabats on the Emagram and the θ-Z diagram. Why do they tilt in opposite directions on these two diagrams?
E13. To compare the many different thermo diagrams at the end of this chapter, first make a copy of each large blank diagram. Then, on each one, plot the same air parcel (P, T, Td) = (90 kPa, 20°C, 10°C). If the parcel is lifted to a pressure of 50 kPa, find the final thermodynamic state of the parcel, and compare the answers from the different diagrams.
E14. The sounding in Figure 5.14e has lines connecting the data points. For each line segment, label its lapse rate (subadiabatic, adiabatic, superadiabatic). Is there a perfect relationship between lapse rate and the static stability indicated in that figure? If not, why not?
E15. Discuss the nature of the Brunt-Väisälä frequency in air that is statically unstable.
E16. The equation for the Brunt-Väisälä oscillation period contains 2π. Why?
E17.
- Check the units of the factors in the Richardson number equations (5.9) to confirm that the Richardson number is indeed dimensionless.
- What is the value of Richardson number for statically unstable air? What does this value imply about turbulence?
- What is the value of Richardson number for an air layer with no wind shear? What does this value imply about turbulence?
E18. Although the large thermo diagrams at the end of this chapter include pressures greater than 100 kPa, most of the smaller diagrams earlier in the chapter have a max pressure of 100 kPa at the bottom of the diagram. For these smaller diagrams, what methods can you use to plot pressures that are more than 100 kPa?
E19. If mixing ratio is conserved in an unsaturated rising air parcel, why isn’t saturated mixing ratio conserved?
E20(§). (This exercise is lengthy.) For pressures in the range of 100 to 10 kPa, use a computer spreadsheet to create a:
- Stüve diagram. [Hint: use (Po/P)ℜd/Cpd as vertical coordinate.]
- Skew-T diagram.
- Tephigram. [Hint: plot it in tilted form, as in Figure 5.2, but with moist adiabats and isohumes added to the other lines in that figure. This is a very difficult exercise.]
- θ-Z diagram. [Hint, plot all the isopleths except the isobars.]
E21(§). Use a computer spreadsheet to create an Emagram for a wider range of pressures (120 kPa to 5 kPa) than I had plotted in my small thermo diagrams. Plot only 1 dry adiabat (θ = 0°C) and 1 isohume (r = 10 g kg–1) for this exercise.
E22. How would the air parcel line in Figure 5.12 be different if the rising parcel entrains a small amount of environmental air as it rises? Sketch this new path on a similar diagram.
E23. For a layer of isothermal air, what is the sign of the Richardson number?
E24. How are the gradient, bulk, and flux Richardson numbers related? The chapter on the Atmospheric Boundary Layer defines the flux Richardson number, and also describes K-theory, a tool you might find useful in answering this question.
E25. Create a new conceptual algorithm different from the “Guide” in this chapter to help you identify different thermo diagram types. Test it to ensure that it doesn’t falsely identify some diagrams.
E26(§). Use a spreadsheet to reproduce Figure 5.2, using the relationship for potential temperature as a function of T and P as given in the Heat chapter.
E27. All the dry adiabats in a Stüve diagram converge to a point above the top left of the diagram. Explain why or why not the dry adiabats in an Emagram converge to a point.
E28. Suppose that turbulent mixing in a dynamically unstable, but statically stable, environment causes both ∆T/∆z and ∆U/∆z to be reduced by the same fraction, b. Show how the Richardson number increases as b decreases. Use this to explain why turbulence acts to reduce the dynamic instabilities that caused it, analogous to LeChatelier’s principle. (Hint: Assume V = 0 for simplicity.)
E29. Figure 5.10 indicates state changes due to fallout of precipitation.
- Can the opposite happen? Namely, can precipitation fall INTO an air parcel, with all of the water staying in the air? If so, give an example and show how that process would be plotted on a thermo diagram.
- What happens if rain from above falls through an air parcel with zero or partial evaporation? Namely, the rainfall does not change during its passage through the air parcel. Indicate this on a thermo diagram.
5.10.4. Synthesize
S1. What if you multiply the numerator and denominator of equation (5.9c) by 0.5·m, where m is air-parcel mass. Describe how the numerator and denominator could be interpreted as potential energy and kinetic energy, respectively.
S2. Use the internet to uncover a brief history of Archimedes. Where did he live? What discoveries did he make, and which were relevant to meteorology? What is he most famous for? What was his role in the wars that were waged at that time?
S3. What if water-vapor condensation caused cooling instead of warming. Describe any possible changes in climate and weather. Draw a rough thermodynamic diagram by eye for this physical situation.
S4. Describe any possible changes in climate and weather if buoyancy force was a function of only air-parcel temperature and not on temperature difference?
S5. Figure 5.17 showed Kelvin-Helmholtz (K-H) waves that form and break in the atmosphere. These are a type of interfacial waves that form on interfaces between dense (cold) air and less-dense (warm) air. Another type of wave called “internal wave” can exist in statically stable air. Use the internet to learn more about internal waves — waves that can move vertically as well as horizontally. Write a brief summary of internal waves.
S6. Describe how the Richardson number would be different if vertical velocity were included in the denominator. Speculate on why it is not included?
S7. Describe any changes in climate and weather that might occur if only Earth’s air warmed due to global warming without any associated change in surface temperature. Justify your hypothesis in terms of static stability.
S8. Suppose a nuclear war happened on Earth, and that many of the explosions caused small-diameter dust particles to be blown into the stratosphere where they would settle out very slowly. This situation is called nuclear winter. Using the principles you learned in the radiation chapter, describe how stratospheric and lower-tropospheric temperatures might change under this thick layer of dust. Describe any changes in climate and weather associated with the resulting changes in atmospheric static stability.
S9. An isentropic chart shows the altitude (either z or P) of a constant θ surface. Describe how you would use upper-air soundings from different weather stations to get the data needed to draw an isentropic chart.
S10. Devise a new type of thermo diagram that has log(r) along the abscissa, and log(P) along the ordinate with scale reversed (max and bottom and min at top). Plot the isotherms and dry adiabats in this diagram. Name the diagram after yourself, and explain the virtues and utility of your diagram.
S11. What if Td could be greater than T in a sounding. Explain how that might be possible, and describe how convective clouds might be different, if at all.
S12. Suppose the tropopause was touching the ground everywhere on Earth. How would the weather or climate be different, if at all?


