4.3: Lagrangian Budgets
- Page ID
- 9550
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Moist air parcels have two additional properties that were unimportant for dry air. One is the amount of water in the parcel, which is important for determining cloud formation and precipitation amounts. The second is the latent heat released or absorbed when water changes phase, which is critical for determining the buoyancy of air parcels and the energy of thunderstorms.
4.4.1. Water Budget
4.4.1.1. Lagrangian Water Conservation
Suppose that the amount of precipitation falling out of the bottom of an air parcel differs from the amount falling into the air parcel from above. This difference gives a net source or sink S**, causing the total water to change inside the air parcel:
\(\ \begin{align} \frac{\Delta r_{T}}{\Delta t}=S^{* *}\tag{3.34}\end{align}\)
For situations where S** = 0, then total water conservation requires that :
\(\ \begin{align} \left(r+r_{i}+r_{L}\right)_{i n i t i a l}=\left(r+r_{i}+r_{L}\right)_{f i n a l}\tag{4.35a}\end{align}\)
If the warm cloud contains no suspended ice crystals, then:
\(\ \begin{align} \left(r+r_{L}\right)_{i n i t i a l}=\left(r+r_{L}\right)_{f i n a l}\tag{4.35b}\end{align}\)
Namely, an increase in the amount of water in one phase (ice, liquid, vapor) must be compensated by a decrease on other phases in order to satisfy total-water conservation if there are no sources or sinks. For an adiabatic process (i.e., no mixing of air or transfer of precipitation across the boundary of an air parcel), rT must be conserved. For this reason, isohumes of total water are included on thermo diagrams.
4.4.1.2. Isohumes on a Thermo Diagram
Thermo diagrams were introduced as Figure 3.3 in the Thermodynamics chapter. On that diagram, the state of the air was represented by two sets of thin solid green lines: isobars (horizontal lines) for pressure and isotherms (vertical lines) for temperature. To that background we will now add another state line: isohumes (thin dotted blue lines) for moisture state of the air (Figure 4.7).
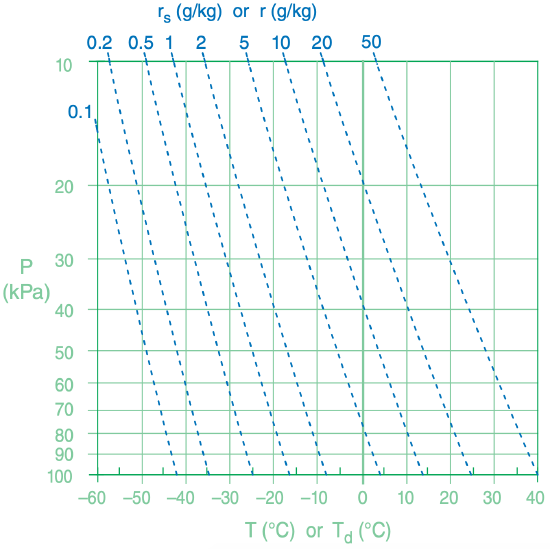
These isohumes are overloaded with information. As a “state” line, the isohume gives the saturation mixing ratio rs at any given temperature and pressure. As a “process” line, the isohume shows how total water mixing ratio rT is conserved for adiabatically rising or sinking air parcels.
To use the thermo-diagram background of P vs. T for isohumes, we need to describe rs as a function of P and T [abbreviate as rs(P, T)]. Eq. (4.5) gives rs(P, es) and the Clausius-Clapeyron eq. (4.1) gives es(T). So combining these two equations gives rs(P, T).
But to draw any one isohume (i.e., for any one value of rs), we need to rearrange the result to give T(P, rs):
\(\ \begin{align} T=\left[\frac{1}{T_{o}}-\frac{\Re_{v}}{L_{v}} \cdot \ln \left\{\frac{r_{s} \cdot P}{e_{o} \cdot\left(r_{s}+\varepsilon\right)}\right\}\right]^{-1}\tag{4.36}\end{align}\)
where To = 273.15 K, eo = 0.6113 kPa, ℜv/L = 0.0001844 K–1, and ε = 0.622 g g–1. This eq. requires that rs be in g g–1 (not g kg–1 ). T has units of Kelvin.
Thus, pick any fixed rs to plot. Then, for a range of P from the bottom to the top of the atmosphere, solve eq. (4.36) for the corresponding T values. Plot these T vs. P values as the isohume line on a thermo diagram. Use a spreadsheet to repeat this calculation for other values of rs, to plot the other isohumes.
Eqs. (4.36) with (4.15b) are similar. Thus, you can use isohumes of T(P, rs) to also represent isohumes of Td(P, r). Namely, you can use isohumes to find the saturation state rs of the air at any P and T, and you can also use the isohumes to describe the process of how Td changes when an air parcel of constant r rises or descends to an altitude of different P.
Sample Application
Find the dew-point temperature of air having mixing ratio of 10 g kg–1 at an altitude where P = 40 kPa.
Find the Answer
Given: r = 10 g kg–1 , P = 40 kPa
Find: Td = ?°C
Apply eq. (4.15b):
\(T_{d}=\left[\frac{1}{273.15 \mathrm{K}}-0.000184 \mathrm{K}^{-1}\right. \cdot
\left.\ln \left\{\frac{(0.01 \mathrm{g} / \mathrm{g}) \cdot(40 \mathrm{kPa})}{(0.6113 \mathrm{kPa}) \cdot(0.01+0.622 \mathrm{g} / \mathrm{g})}\right\}\right]^{-1}\)
= [ (0.003661 K–1) – (0.0001844 K–1)·ln{1.035}]–1
= [0.003655 K–1]–1 = 273.6 K ≈ 0.5°C
Check: Physics and units are reasonable.
Exposition: You could have saved a lot of time and effort by just looking up the answer in Figure 4.7. Namely, find the point where the 10 g kg–1 mixing-ratio diagonal line intersects the 40 kPa isobar, and then read vertically straight down to find Td.
We would have found the same numerical answer if we asked for the temperature corresponding to air at 40 kPa that is saturated with rs = 10 g kg–1 with rL = 0. For this situation, we would have used eq. (4.36).
4.4.2. Heat Conservation for Saturated Air
4.4.2.1. Moist Adiabatic Lapse Rate
Saturated air is air that is foggy or cloudy, with an amount of water vapor equal to the maximum amount that air can hold given the parcel’s temperature. The air parcel contains both vapor and small suspended liquid water droplets or ice crystals. Consider an adiabatic process for which: (1) the parcel does not mix with its surroundings; (2) there is no transfer of heat to/from the parcel from outside; and (3) no liquid (or solid) water falls out of or into the parcel.
An air parcel rising adiabatically has two competing processes that affect its temperature. As for the unsaturated parcel, the saturated parcel expands into regions of lower pressure, doing work on the atmosphere at the expense of thermal energy stored in the parcel. But the colder air parcel can hold less water vapor at saturation than it carried up from the altitude below. So more of the vapor condenses, for which: (1) the latent heating partially offsets the expansion cooling; and (2) the amount of condensed water droplets or ice increases.
The converse occurs for adiabatic descent, where cooling from evaporating liquid-water droplets partially offsets warming due to adiabatic compression.
For air rising across height increment ∆z, a saturated parcel has less temperature decrease ∆T than does a dry (unsaturated) parcel. Conversely, for air descending across height increment ∆z, a saturated parcel has less temperature increase ∆T than does a dry parcel.
While we previously saw that the dry adiabatic lapse rate was constant (Γs = –∆T/∆z = 9.8 °C km–1 ), we are not so lucky for the saturated lapse rate, which varies with altitude and air temperature.
A saturated air parcel that rises adiabatically has a temperature decrease with increasing height of –∆T/∆z = Γs , where Γs saturated (or moist) adiabatic lapse rate. This rate is given by:
\(\ \begin{align} \Gamma_{s}=\frac{|g|}{C_{p}} \cdot \frac{\left(1+\frac{r_{s} \cdot L_{v}}{\Re_{d} \cdot T}\right)}{1+\frac{L_{v}^{2} \cdot r_{s} \cdot \varepsilon}{C_{p} \cdot \Re_{d} \cdot T^{2}}}\tag{4.37a}\end{align}\)
Compare typical saturated adiabatic lapse-rate values of 4 to 7°C km–1 to the dry adiabatic lapse rate of 9.8°C km–1.
Instead of a change of temperature with height, this saturated adiabatic lapse rate can be rewritten as a change of temperature ∆T with change of pressure ∆P:
\(\ \begin{align} \frac{\Delta T}{\Delta P}=\frac{\left[\left(\Re_{d} / C_{p}\right) \cdot T+\left(L_{v} / C_{p}\right) \cdot r_{s}\right]}{P \cdot\left(1+\frac{L_{v}^{2} \cdot r_{s} \cdot \varepsilon}{C_{p} \cdot \Re_{d} \cdot T^{2}}\right)}\tag{4.38a}\end{align}\)
For the equations above, don’t forget that specific heat Cp varies with humidity (see eq. 3.2).
After plugging in the values for the thermodynamic constants and assuming Cp ≈ constant, eq. (4.37a) can be simplified as:
\(\ \begin{align} \Gamma_{s}=\Gamma_{d} \cdot \frac{\left[1+\left(a \cdot r_{s} / T\right)\right]}{\left[1+\left(b \cdot r_{s} / T^{2}\right)\right]}\tag{4.37b}\end{align}\)
where a = 8711 K, b = 1.35x107 K2, and Γd = 9.8 K km–1. Eq. (4.37b) differs from (4.37a) by roughly 1%, so it is often accurate enough for most applications. Use g g–1 for mixing ratio, and use Kelvin for temperature. Be aware that rs is not constant, but is a function of temperature.
Similarly, eq. (4.38a) simplifies to:
\(\ \begin{align} \frac{\Delta T}{\Delta P}=\frac{\left[a \cdot T+c \cdot r_{s}\right]}{P \cdot\left[1+\left(b \cdot r_{s} / T^{2}\right)\right]}\tag{4.38b}\end{align}\)
with a = 0.28571, b = 1.35x107 K2 , and c = 2488.4 K.
4.4.2.2. Moist Adiabats on a Thermo Diagram
In the Thermodynamics chapter we discussed the process of “dry” adiabatic vertical motion, where “dry” means unsaturated humid air. We had plotted those process lines as the dry adiabats in the thermo diagram of Figure 3.4.
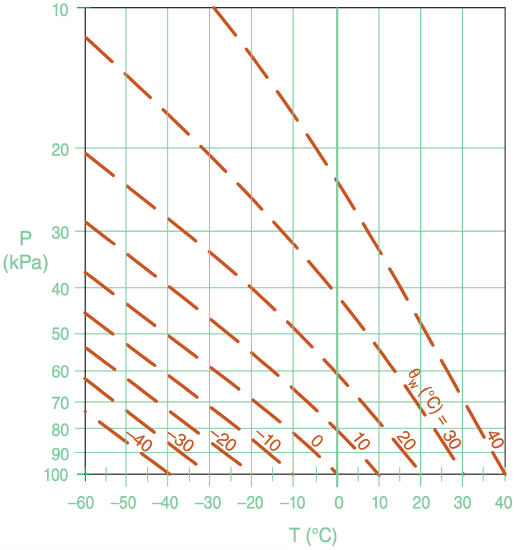
We can now use eq. (4.38) to calculate and plot the corresponding moist adiabats (also called saturated adiabats) that apply for saturated (cloudy or foggy) vertical motion. The saturated adiabats are rather complicated to calculate, because the equations above give the slope (∆T/∆P) for the moist adiabat rather than the desired value of T at each P. But don’t despair — we can still find the moistadiabat curves by iterating each curve upward.
Start at P = 100 kPa with some initial value for T. First use these with eq. (4.5) to get rs. Use these in eq. (4.38) to get ∆T/∆P. Then apply that over a small increment of pressure (such as ∆P = P2 – P1 = –0.2 kPa) to solve for the new T2 at P2 using:
\(\ \begin{align} T_{2}=T_{1}+\frac{\Delta T}{\Delta P} \cdot\left(P_{2}-P_{1}\right)\tag{4.39}\end{align}\)
Repeat by using the new T2 at P2 to find the new rs2, and use all these numbers to solve for a new (∆T/∆P)2, and use eq. (4.39) again to take the next step. Repeat to iterate your way up the moist adiabat. The result is one of the curves in Figure 4.8.
To get other curves, start over with a different initial value of T at P = 100 kPa, as shown in Figure 4.8. Each of those curves is identified by its initial T at the reference pressure of 100 kPa. The next section shows that these labels are called wet-bulb potential temperature θw.
Sample Application
What is the value of moist-adiabatic lapse rate at T = 10°C and P = 70 kPa? Do this calculation using both (a) Cp = Cp dry and (b) the actual moist Cp. (c) Also find ∆T/∆P for a rising saturated air parcel.
Find the Answer
Given: P = 70 kPa, T = 10°C = 283.15 K ,
Find: Γs = ? °C km–1
(a) Apply eq. (4.37b). But this eq. needs rs, which we first can find using eq. (4.5). In turn, that eq. needs es, which we can get from Table 4-1: es = 1.232 kPa at T = 10°C. Plug this into eq. (4.5): rs = (0.622 g/g)·(1.232 kPa) / (70kPa – 1.232 kPa) = 0.01114 g/g.
Finally, use this in eq. (4.37b):
\(\Gamma_{s}=\frac{\left(9.8 \frac{\mathrm{K}}{\mathrm{km}}\right) \cdot\left[1+\frac{(0.01114 \mathrm{g} / \mathrm{g}) \cdot(8711 \mathrm{K})}{283.15 \mathrm{K}}\right]}{\left[1+\frac{\left(1.35 \times 10^{7} \mathrm{K}^{2}\right) \cdot(0.01114 \mathrm{g} / \mathrm{g})}{(283.15 \mathrm{K})^{2}}\right]}\)
Γs = (9.8 K km–1)·[1.3427] / [2.8758] = 4.58 K km–1.
(b) Apply eq. (3.3) for saturated air (for which r = rs):
Cp = Cp dry · [1 + 1.84r] = (1004 J·kg–1·K–1)· [1+1.84·(0.01114g/g] = 1024.6 J·kg–1·K–1.
Thus: |g|/Cp = 9.565 K km–1
Lv/Cp = 2440. K.
Lv/ℜd = 8711 K.
When these are applied in eq. (4.37a), the result is:
\(\Gamma_{s}=\frac{\left(9.565 \frac{\mathrm{K}}{\mathrm{km}}\right) \cdot\left[1+\frac{(0.01114 \mathrm{g} / \mathrm{g}) \cdot(8711 \mathrm{K})}{283.15 \mathrm{K}}\right]}{\left[1+\frac{(2440 \mathrm{K}) \cdot(8711 \mathrm{K}) \cdot(0.01114 \mathrm{g} / \mathrm{g}) \cdot 0.622}{(283.15 \mathrm{K})^{2}}\right]}\)
Γs = (9.565 K km–1)·[1.3427]/[2.837] = 4.53 K km–1
(c) If we assume Cp ≈ Cp dry, then apply eq. (4.38b):
\(\frac{\Delta T}{\Delta P}=\frac{[0.28571 \cdot(283.15 K)+(2488.4 K \cdot(0.01114 g))]}{P \cdot\left[1+\left[1.35 \times 10^{7} K^{2} \cdot(0.01114 g / g) /(283.15 K)^{2}\right]\right]}\)
= [108.62 / (1 + 1.876 )] / P = (37.77K) / P
At P = 70 kPa the result is = ∆T/∆P = 0.54 K kPa–1
Check: Physics and units are reasonable.
Exposition: Don’t forget for answers (a) and (b) that lapse rates are the rate of temperature decrease with altitude. Parts (a) and (b) give nearly identical answers, implying that eq. (4.37b) is sufficiently accurate for most applications.
Normally, pressure decreases as altitude increases, thus answer (c) also gives cooling for negative ∆P.
As for the dry adiabats, it is useful to see how moist adiabats can be calculated using a computer spreadsheet. The following example is for the moist adiabat that starts at T = 30°C at P = 100 kPa.
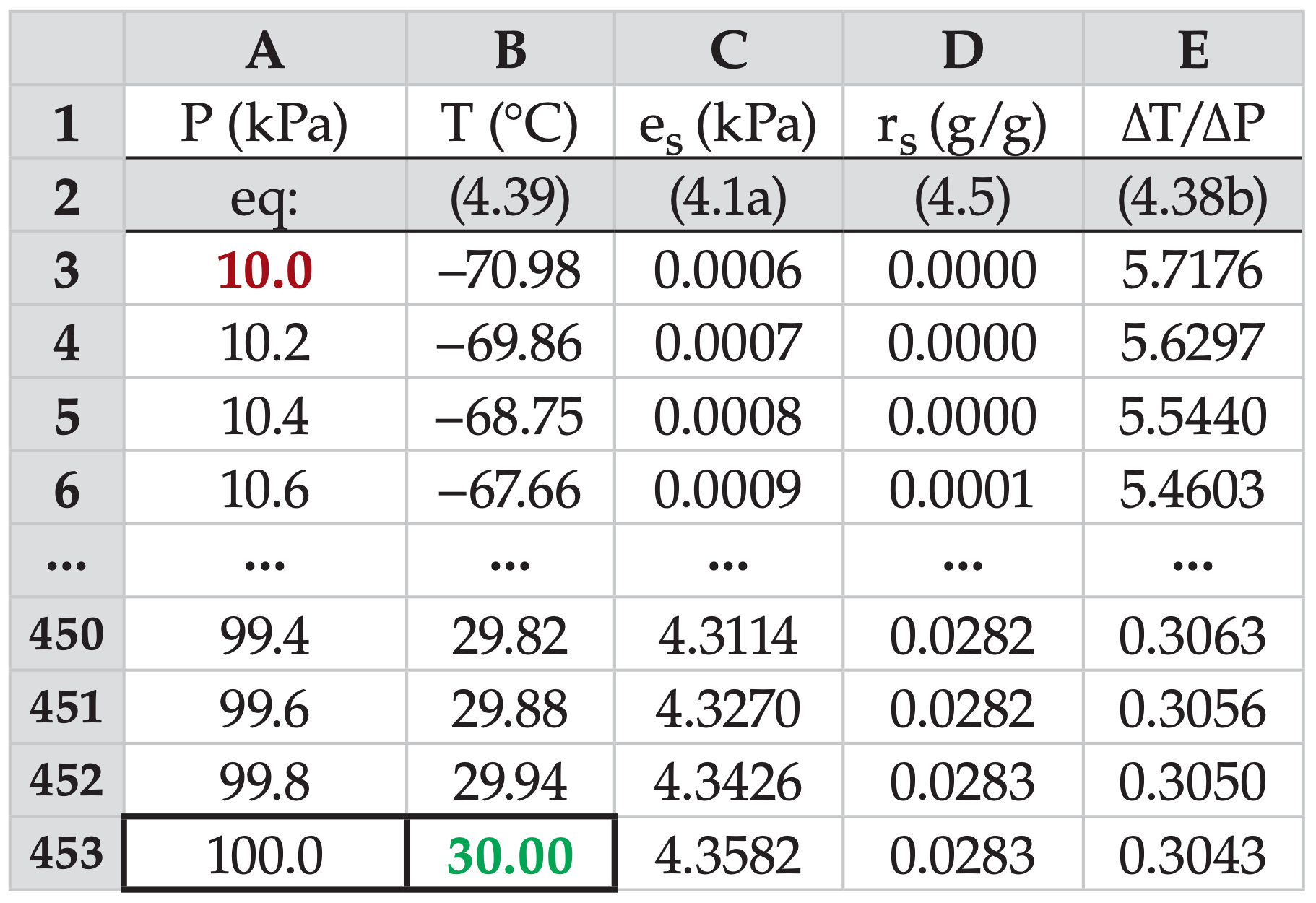
In row 1, label the variables at the top of the 5 columns as I have done here. In row 2, identify which equation numbers you are using, as documentation for you or others who use your calculations later.
In row 3 column A, enter the pressure at the top of the atmospheric column of interest: 10.0 (kPa), shown in red in this example. In row 4 column A type the next pressure 10.2 (kPa), which is the starting pressure plus increment ∆P = 0.2 kPa. Then use automatic series generating methods in your spreadsheet to extend this series down to the point where the pressure is 100.0 (kPa), (on row 453 in my spreadsheet).
Next, in row 453 column B, type in the starting temperature of 30 (°C) for this moist adiabat. In (row, col) = (453, C), use the Clausius-Clapeyron eq. (4.1a) to calculate the saturation vapor pressure for the pressure in column A, and don’t forget to convert temperature to Kelvin in your spreadsheet equation. Similarly, use eq. (4.5) to calculate the saturation mixing ratio in cell (453, D). Use eq. (4.38b) to find the moist-adiabat slope in cell (453, E). Again, use Kelvin in your eqs.
For the next row up, but only in cell (452,B), use eq. (4.39) to find the new temperature along the moist adiabat. Be sure to check that the sign is correct (i.e., that temperature is decreasing, not increasing). Then, use the “fill-up” spreadsheet command to fill the eqs. from cells (453, C through E) up one row. Finally, use the fill-up command to fill the eqs. from cells (452, B through E) up to the top pressure level in row 3.
Check: Agrees with Figure 4.8 for θw = 30°C.
4.4.2.3. Wet-Bulb, Equivalent, and Liquid-Water Potential Temperatures
Recall from the Thermodynamics chapter that potential temperature θ is conserved during unsaturated adiabatic ascent or descent. However, if an air parcel containing water vapor is lifted above its LCL, then condensation will add latent heat, causing θ to increase. Similarly, if the air contains liquid water such as cloud drops, when it descends some of the drops can evaporate, thereby cooling the air and reducing θ.
However, we can define new variables that are conserved for adiabatic ascent or descent, regardless of any evaporation or condensation that might occur.
One is the equivalent potential temperature θe:
\(\ \begin{align} \theta_{e} \approx \theta+\left(\frac{L_{v} \cdot \theta}{C_{p} \cdot T}\right) \cdot r \approx \theta+\frac{L_{v}}{C_{p d}} \cdot r\tag{4.40}\end{align}\)
Another is liquid water potential temperature, θL:
\(\ \begin{align} \theta_{L} \approx \theta-\left(\frac{L_{v} \cdot \theta}{C_{p} \cdot T}\right) \cdot r_{L} \approx \theta-\frac{L_{v}}{C_{p d}} \cdot r_{L}\tag{4.41}\end{align}\)
where Lv = 2.5x106 J·kg–1 is the latent heat of vaporization, Cp is the specific heat at constant pressure for air (Cp is not constant, see the Thermodynamics chapter), T is the absolute temperature of the air, and mixing ratios (r and rL) have units of (gwater gair–1). The last approximation in both equations is very rough, with Lv/Cpd = 2.5 K·(gwater/kgair)–1.
Both variables are conserved regardless of whether the air is saturated or unsaturated. Consider unsaturated air, for which θ is conserved. In eq. (4.40), water-vapor mixing ratio r is also conserved during ascent or descent, so the right side of eq. (4.40) is constant, and θe is conserved. Similarly, for unsaturated air, liquid water mixing ratio rL = 0, hence θL is also conserved in eq. (4.41).
For saturated air, θ will increase in a rising air parcel due to latent heating, but r will decrease as some of the vapor condenses into liquid. The two terms in the right side of eq. (4.40) have equal but opposite changes that balance, leaving θe conserved. Similarly, the two terms on the right side of eq. (4.41) balance, due to the minus sign in front of the rL term. Thus, θL is conserved.
By subtracting eq. (4.41) from (4.40), we can see how θe and θL are related:
\(\ \begin{align} \theta_{e} \approx \theta_{L}+\left(\frac{L_{v} \cdot \theta}{C_{p} \cdot T}\right) \cdot r_{T}\tag{4.42}\end{align}\)
for a total-water mixing ratio (in g g–1) of rT = r + rL. Although θe and θL are both conserved, they are not equal to each other.
We can use θe or θL to identify and label moist adiabats. Consider an air parcel starting at P = 100 kPa that is saturated but contains no liquid water (r = rs = rT). For that situation θL is equal to its initial temperature T (which also equals its initial potential temperature θ at that pressure). A rising air parcel from this point will conserve θL, hence we could label the moist adiabat with this value (Figure 4.9).
An alternative label starts from same saturated air parcel at P = 100 kPa, but conceptually lifts it to the top of the atmosphere (P = 0). All of the water vapor will have condensed out at that end point, heating the air to a new potential temperature. The potential temperature of the dry adiabat that is tangent to the top of the moist adiabat gives θe (Figure 4.9). [CAUTION: On some thermo diagrams, equivalent potential temperature is given in units of Kelvin.]
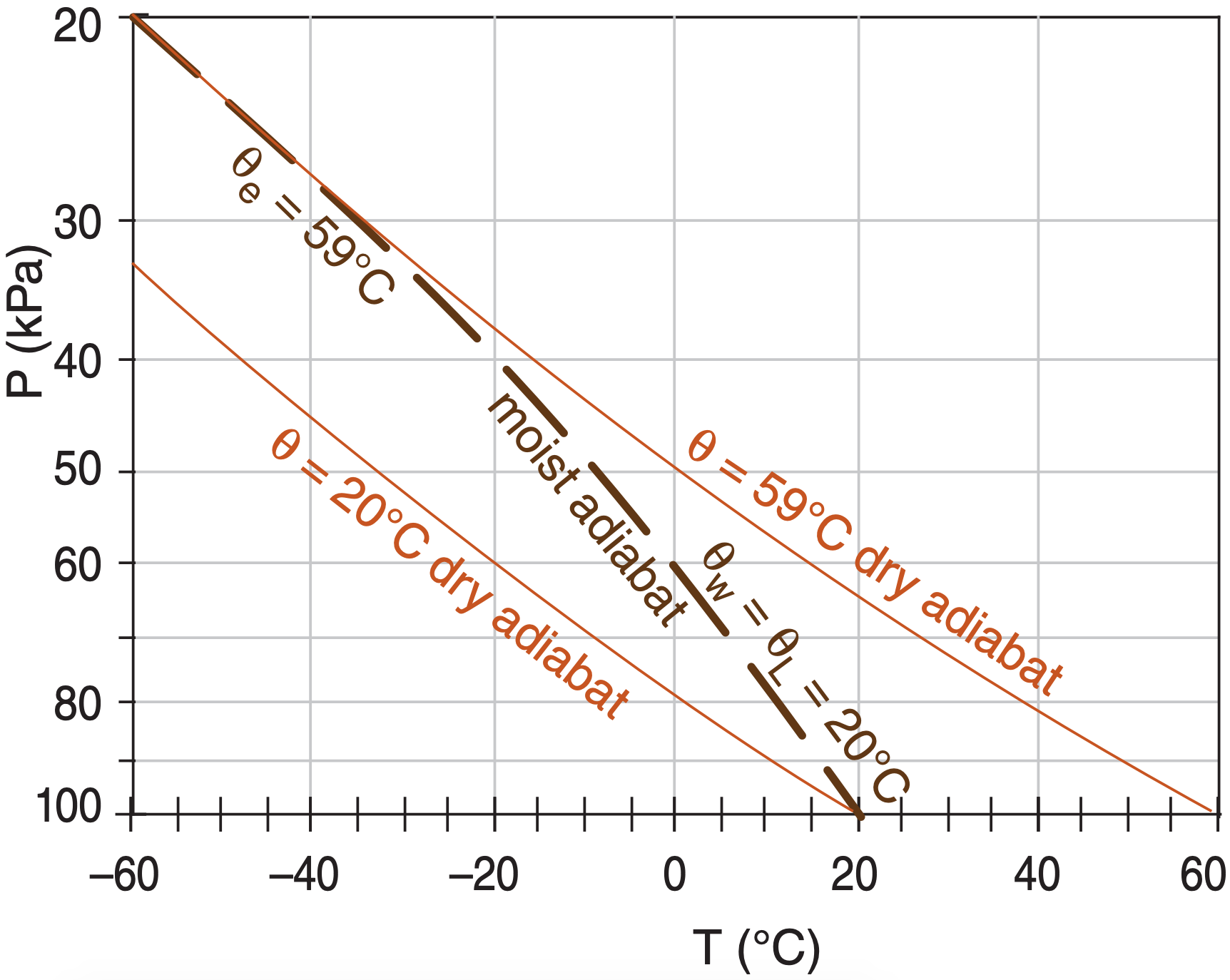
In other words, θL is the potential temperature at the bottom of the moist adiabat (more precisely, at P = 100 kPa), while θe is the potential temperature at the top. Either labeling method is fine — you will probably encounter both methods in thermo diagrams that you get from around the world.
Wet-bulb potential temperature (θw) can also be used to label moist adiabats. For θw, use Normand’s rule on a thermo diagram (Figure 4.10). Knowing temperature T and dew-point Td at initial pressure P, plot these points on a thermo diagram. Next, from the T point, follow a dry adiabat up, and from the Td point, follow an isohume up. Where they cross is the lifting condensation level LCL.
From that LCL point, follow a saturated adiabat back down to the starting altitude, which gives the wet-bulb temperature Tw. If you continue to follow the saturated adiabat down to a reference pressure (P = 100 kPa), the resulting temperature is the wet-bulb potential temperature θw (see Figure 4.10). Namely, θw equals the θL label of the moist adiabat that passes through the LCL point. Labeling moist adiabats with values of wet-bulb potential temperature θw is analogous to the labeling of dry adiabats with θ, which is why I use θw here.
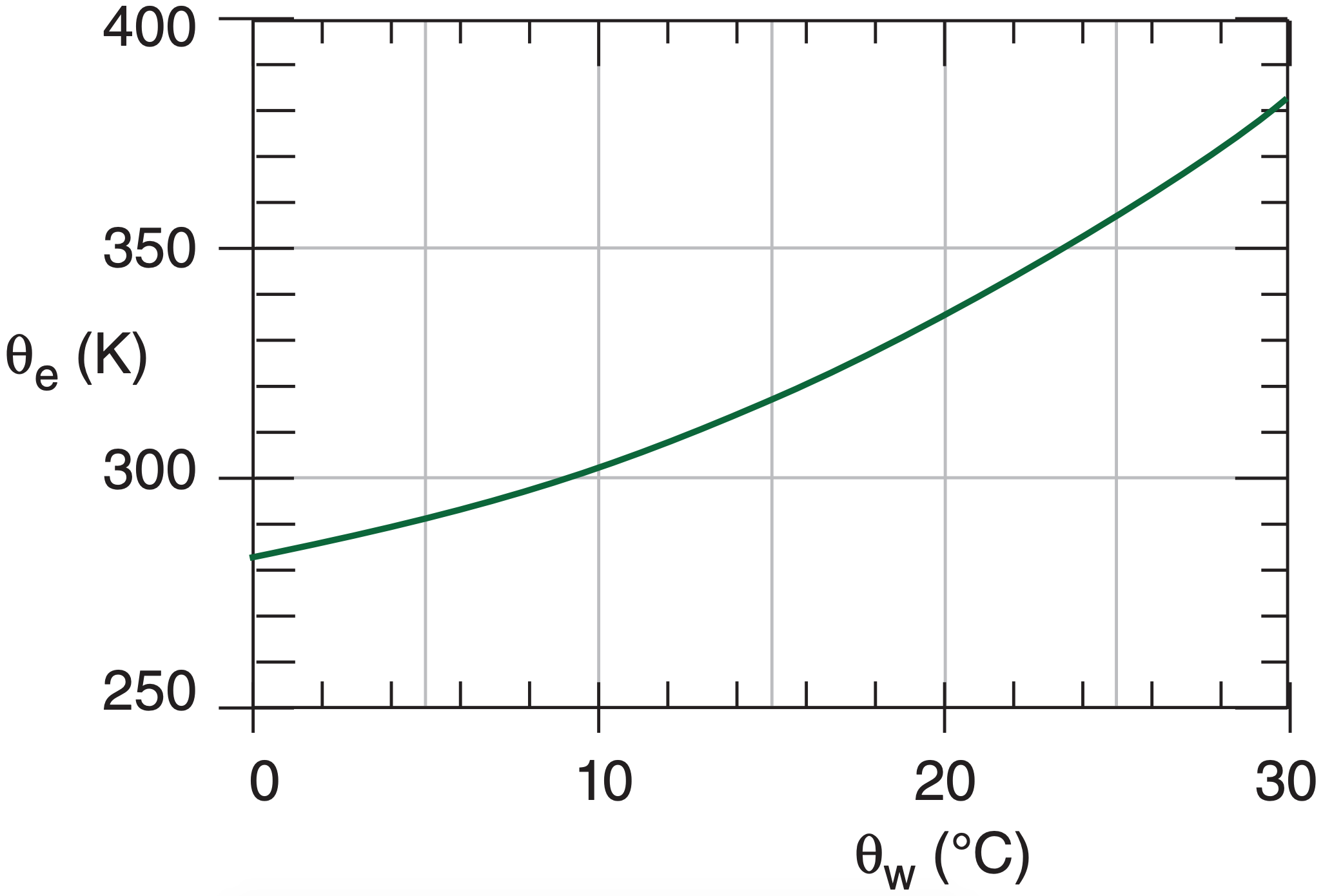
To find θe(K) for a moist adiabat if you know its θw(K), use:
\(\ \begin{align} \theta_{e}=\theta_{w} \cdot \exp \left(a_{3} \cdot r_{s} / \theta_{w}\right)_{o}\tag{4.43a}\end{align}\)
where a3 = 2491 K·kgair kgvapor –1, and rs is initial saturation mixing ratio (kgvapor kgair–1) at T = θw and P = 100 kPa (as denoted by subscript “o”). You can approximate (4.43a) by
\(\ \begin{align} \theta_{e}(\mathrm{K}) \approx a_{o}+a_{1} \cdot \theta_{w}\left(^{\circ} \mathrm{C}\right)+a_{2} \cdot\left[\theta_{w}\left(^{\circ} \mathrm{C}\right)\right]^{2}\tag{4.43b}\end{align}\)
where ao = 282, a1 = 1.35, and a2 = 0.065, for θw in the range of 0 to 30°C (see Figure 4.11). Also the θL label for the moist adiabat passing through the LCL equals this θw.
Sample Application
What lines do dry & saturated air parcels follow on a thermo diagram if they start at P= 100 kPa, T= 40°C?
Find the Answer
Given: P = 100 kPa, T = 40°C initially.
Plot adiabatic process lines for θ = 40°C & θw = 40°C. Copying the lines from Figs. 3.3 & 4.8.

Exposition: Even starting with the same temperature, a rising saturated air parcel becomes warmer than an unsaturated parcel due to latent-heat release.
Sample Application
Air at pressure 80 kPa and T = 0°C is saturated, & holds 2 g kg–1 of liquid water. Find θe and θL.
Find the Answer
Given: P = 80 kPa, T = 0°C = 273.15K , rL = 2 g kg–1.
Find: θe = ? °C, θL = ? °C
First, do preliminary calculations shared by both eqs: Rearrange eq. (3.12) to give:
(θ/T) = (Po/P)0.28571 = (100kPa/80kPa) 0.28571 = 1.066
Thus, θ = 291K ≈ 18°C
At 80 kPa and 0°C, solve eq. (4.5) for rs = 4.7 g kg–1
Then use eq. (3.2):
Cp = Cpd·(1 +1.84·r) = (1004.67 J·kg–1·K–1) ·[1+1.84·(0.0047 g g–1)] = 1013.4 J·kg–1·K–1.
Thus, Lv/Cp = 2467 K/(gwater gair–1)
and (Lv/Cp)·(θ/T) ≈ 2630 K/(gwater gair–1)
Use eq. (4.40):
θe = (18°C) + (2630 K/(gwater gair–1))·(0.0047) = 30.4 °C
Use eq. (4.41):
θL = (18°C) – (2630 K/(gwater gair–1))·(0.002) = 12.7 °C
Check: Physics, units, & magnitude are reasonable.
Exposition: The answers are easier to find using a thermo diagram (after you’ve studied the Stability chapter). For θe , find the θ value for the dry adiabat that is tangent at the diagram top to the moist adiabat. For θL, follow a moist adiabat down to where it crosses the (2 + 4.7 = 6.7 g kg–1) isohume, and from there follow a dry adiabat to P = 100 kPa.
Sample Application
Verify the labels on the moist adiabat that passes through the LCL in Figure 4.10, given starting conditions T = 33°C and Td = 5.4°C at P = 90 kPa.
Find the Answer
Given: T = 33°C ≈ 306K, Td = 5.4°C ≈ 278.4K
Find: θe , θw and θL labels (°C) for the moist adiabat
First, find the initial θ, using eq. (3.12)
First, find the initial θ, using eq. (3.12) θ = T·(Po/P)0.28571 = (306K)·(100kPa/90kPa) 0.28571 = 315.4K = 42.4°C
Next, find the mixing ratio using eq. (4.1b) & (4.4):
e = 0.6114kPa·exp[5423·(1/273.15 – 1/278.4)] =0.889kPa
r ≈ (622g kg–1)·(0.889kPa)/[90–0.889kPa] ≈ 6.2g kg–1
Next, use eq. (3.2) to find Cp = Cpd·(1 +1.84·r)
Cp =(1004.67 J·kg–1·K–1) ·[1+1.84·(0.0062 g g–1)]
Cp = 1016.1 J·kg–1·K–1
Solve the more accurate version of eq. (4.40):
θe = (42.4°C) + {(2500 J gwater –1)·(315.4K)/ [(1016.1 J·kg–1·K–1)·(306K)]} · (6.2 gwater kgair–1)
= (42.4°C) +(2.536 K·kgair gwater –1)·(6.2 gwater kgair–1) = 58.1°C = 331.1 K
The approximate version of eq. (4.40) gives almost the same answer, and is much easier:
θe = (42.4°C) + (2.5 K·kgair gwater –1)·(6.2 gwater kgair–1) = 57.9°C
Eq. (4.43b) is a quadratic eq. that can be solved for θw. Doing this, and then plugging in θe = 331.1 K gives:
θw ≈ 19°C. , which is the label on the moist adiabat.
Using θL ≈ θw :
θL ≈ 19°C.
Check: Physics and units are reasonable
Exposition: These values are within a couple degrees of the labels in Figure 4.10. Disappointing that they aren’t closer, but the θe results are very sensitive to the starting point.
Sample Application
For a moist adiabat of θw = 14°C , find its θe.
Find the Answer
Given: θw = 14°C = 287 K
Find: θe = ? K
First get rs from Figure 4.7 at P = 100 kPa and T = 14°C:
rs = 10 g kg–1 = 0.010 kg kg–1.
Next, use eq. (4.43a):
θe = (287K) · exp[2491(K·kgair kgvapor –1) · (0.010 kgvapor kgair–1) / (287K) ] = 313K
Check: Units are reasonable. Agrees with Figure 4.11.
Exposition: This θe = 40°C. Namely, if a saturated air parcel started with θw = T = 14°C, and then if all the water vapor condensed, the latent heat released would warm the parcel to T = 40°C.
Sample Application
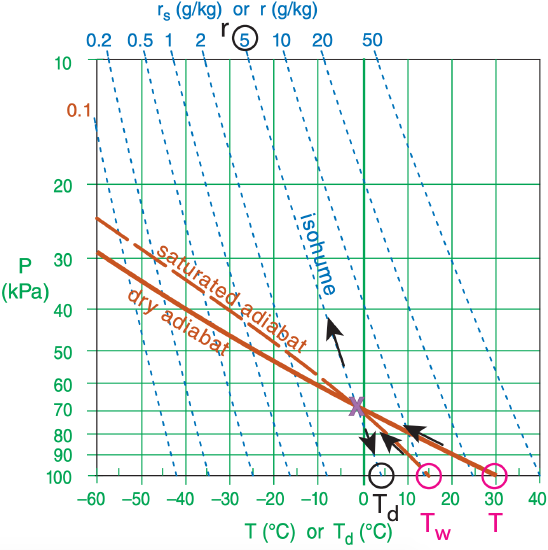
Suppose a psychrometer at 100 kPa measures drybulb and wet-bulb temperatures of 30°C and 15°C. Use a thermo diagram to find the values of Td and r ?
Find the Answer
Given: P = 100 kPa, T = 30°C, Tw = 15°C.
Find: r = ? g kg–1 , Td = ?°C
Hint: We can use the opposite of Normand’s rule.
We will learn more about thermo diagrams in the next chapter. So this exercise gives us a preview.
To use Normand’s rule in reverse, follow a dry adiabat up from the starting dry-bulb temperature, and follow a saturated adiabat up from the starting wet-bulb temperature. Where they cross, follow the isohume down to the starting altitude to find the dewpoint temperature, or follow the isohume up to read the isohume’s mixing-ratio value.
Figure 3.4 shows many dry adiabats, but not the one we want. So I interpolated between the 20 and 40°C dry adiabats, and copied and pasted the result (as the solid dark-orange line for θ = 30°C) onto copy of Figure 4.7, as shown below. A magenta circle indicates the starting temperature and pressure.
Figure 4.8 shows many saturated adiabats, but not the one we want. So I interpolated between the 10 and 20°C saturated adiabats, and copied and pasted the result into the figure below as the dark-orange dashed line for θw = 15°C. Another magenta circle indicates the starting wet-bulb temperature and pressure.
Those two lines cross (see purple “X” in the figure) almost exactly on the r = 5 g kg–1 isohume (see black circle at top of diagram. Following that same isohume down to P = 100 kPa gives Td ≈ 4°C (circled in black).
Check: Physics and unit are reasonable.
Exposition: The “X” is the location of the lifting condensation level (LCL), which is about 68 kPa in this diagram.