10.9: Kinematics
- Page ID
- 10200
Kinematics is the study of patterns of motion, without regard to the forces that cause them. We will focus on horizontal divergence, vorticity, and deformation. All have units of s–1.
We have already encountered horizontal divergence, D, the spreading of air:
\(\ \begin{align} D=\frac{\Delta U}{\Delta x}+\frac{\Delta V}{\Delta y}\tag{10.72}\end{align}\)
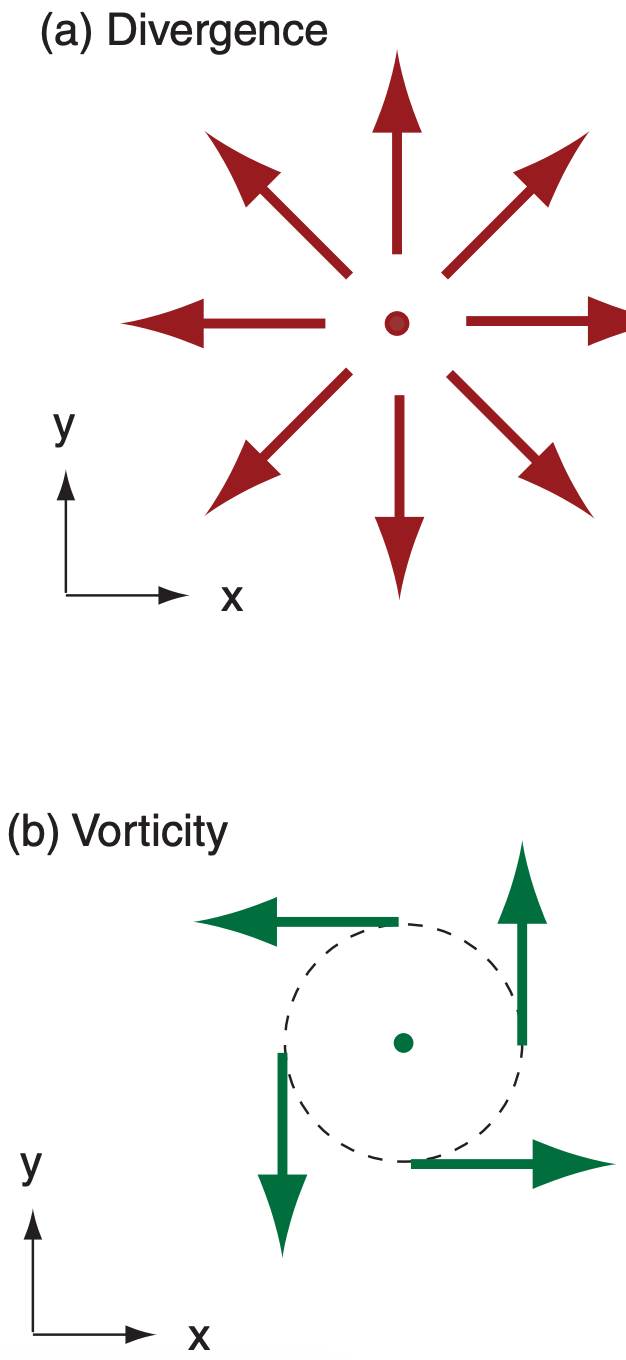

Figure 10.29a shows an example of pure divergence. Its sign is positive for divergence, and negative for convergence (when the wind arrows point toward a common point).
Vorticity describes the rotation of air (Fig. 10.29b). The relative vorticity, ζr , about a locally vertical axis is given by:
\(\ \begin{align} \zeta_{r}=\frac{\Delta V}{\Delta x}-\frac{\Delta U}{\Delta y}\tag{10.73}\end{align}\)
The sign is positive for counterclockwise rotation (i.e., cyclonic rotation in the N. Hemisphere), and negative for clockwise rotation. Vorticity is discussed in greater detail in the General Circulation chapter. Neither divergence nor vorticity vary with rotation of the axes — they are rotationally invariant.
Two types of deformation are stretching deformation and shearing deformation (Figs. 10.29c & d). Stretching deformation, F1, is given by:
\(\ \begin{align} F_{1}=\frac{\Delta U}{\Delta x}-\frac{\Delta V}{\Delta y}\tag{10.74}\end{align}\)
The axis along which air is being stretched (Fig. 10.29c) is called the axis of dilation (x axis in this example), while the axis along which air is compressed is called the axis of contraction (y axis in this example).
Shearing deformation, F2, is given by:
\(\ \begin{align} F_{2}=\frac{\Delta V}{\Delta x}+\frac{\Delta U}{\Delta y}\tag{10.75}\end{align}\)
As you can see in Fig. 10.29d, shearing deformation is just a rotated version of stretching deformation.
The total deformation, F, is:
\(\ \begin{align} F=\left[F_{1}^{2}+F_{2}^{2}\right]^{1 / 2}\tag{10.76}\end{align}\)
Deformation often occurs along fronts. Most real flows exhibit combinations of divergence, vorticity, and deformation.


