6.6: What is the origin of the Planck Function?
- Page ID
- 3387
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recall that molecules have a wide range of speeds and thus a wide range of energies. The Maxwell–Boltzmann Distribution, which gives the distribution of molecules as a function of energy, is given approximately by the equation:
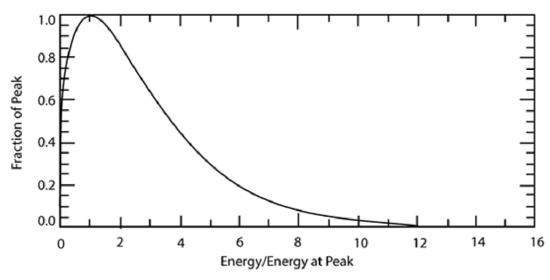
\[f(E)=\frac{2 \sqrt{E}}{\sqrt{\pi}(k T)^{3 / 2}} \exp (-E / k T)\]
where f is the probability that a molecule has an energy within a small window around E, T is the absolute temperature, and k is the Boltzmann constant. The above equation, when integrated over all energies, gives the value of 1.
The functional form of this distribution is shown below:
All objects—gas, liquid, or solid—emit radiation. If we think of radiation as photons, we would say that these photons have a distribution of energies, just like molecules do. However, photons cannot have continuous values of photon energy; instead, the photon energy is quantized, which means that it can have only discrete energy values that are different by a very very small amount of energy. When this quantized distribution is assumed, then the distribution of spectral irradiance leaving a unit area of the object’s surface per unit time per unit wavelength interval into a hemisphere is called the Planck Distribution Function of Spectral Irradiance:
\[P_{e}(\lambda)=\frac{2 \pi h c^{2}}{\lambda^{5}} \frac{1}{\exp (h c / \lambda k T)-1}\]
where h is Planck’s constant, c is the speed of light, k is the Boltzmann constant (1.381 x 10–23 J K–1), T is the absolute temperature, and λ is the wavelength. The integral of this function over all wavelengths leads to the Stefan–Boltzmann Law Irradiance, which gives the total radiant energy per unit time per unit area of the object’s surface emitted into a hemisphere.
Pe(λ)/π is called the Planck Distribution Function of Spectral Radiance and commonly has units of W steradian–1m–2 nm–1 and is often denoted by the letter I. A steradian is just a unit solid angle. Just as a radian for a circle is a length of the circle's arc that is equal to the circle's radius, a steradian is the area on a sphere's surface that is equal to the sphere's radius squared. There are 2π radians along a circle and 4π steradians (abbreviated sr) over a sphere. For some of this discussion we will use the spectral irradiance Pe(λ) and consider the radiation from any area on the sphere to be emitted not in a single direction but into the full hemisphere of directions. Later on, when we start talking about absorption, we will need to think about the irradiance in very specific directions, in which case we will use radiance. Be mindful of the difference between irradiance and radiance.
The spectral irradiance is the amount of energy that is emitted from or falling on a unit area in space per unit time per unit wavelength (W m–2 µm–1). So the m2 in this case indicates a surface area on which energy is leaving or falling. To get the Sun’s spectral irradiance at the top of Earth’s atmosphere, we must multiply the spectral irradiance emitted by the Sun's surface by the Sun's surface area to get the total energy emitted per unit time and per unit wavelength by the Sun and then divide by the surface area of the sphere that has a radius equal to the Earth–Sun distance to get the energy per time per unit wavelength per unit area of the surface located at the top of Earth's atmosphere.
Physical Interpretation
All the radiation that is emitted from the Sun’s surface continues to move outward at the speed of light until it hits objects, but there are very few objects between the Sun and Earth, except occasionally the Moon. Thus, in the absence of any objects, the total amount of solar irradiance striking the planets decreases as the square of the distance between the center of the Sun and the surface of the planet.
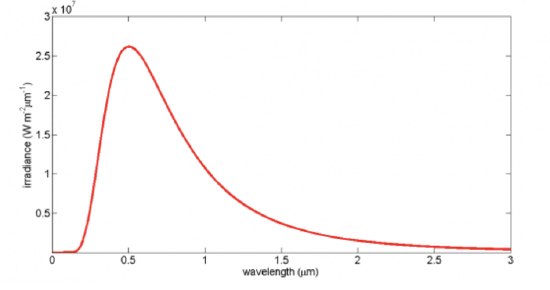
The Planck distribution function spectral irradiance for an object at a temperature of 5777 K (the Sun's surface temperature) is shown in the figure below. Note the rapid rise at the shorter wavelengths, the peak value, and then the slower decline at longer wavelengths. Look at the peak value of the irradiance, which is about 25 million W m–2 nm–1! That's a lot of energy being radiated from the Sun's surface, but of course the Earth is 150 million km away from the Sun and thus intercepts less than half a billionth of the solar irradiance.