22.6: Mirages
- Page ID
- 10982
Refractive index nair varies with air density ρ:
\begin{align}n_{a i r}-1 \approx\left(n_{r e f}-1\right) \cdot \rho / \rho_{r e f}\tag{22.24}\end{align}
where ref denotes a reference condition (such as given for air at any of the T and P values in Table 22-1). Knowing T and P, you can use the ideal gas law to find density [ρ = P/(ℜ·T) for ℜ = 0.287 (kPa K–1)·(m3 kg–1); see Chapter 1 for details]. Thus, you can rewrite eq. (22.24) as:
\begin{align}n_{a i r}-1=\left(n_{r e f}-1\right) \cdot \frac{T_{r e f}}{T} \cdot \frac{P}{P_{r e f}}\tag{22.25}\end{align}
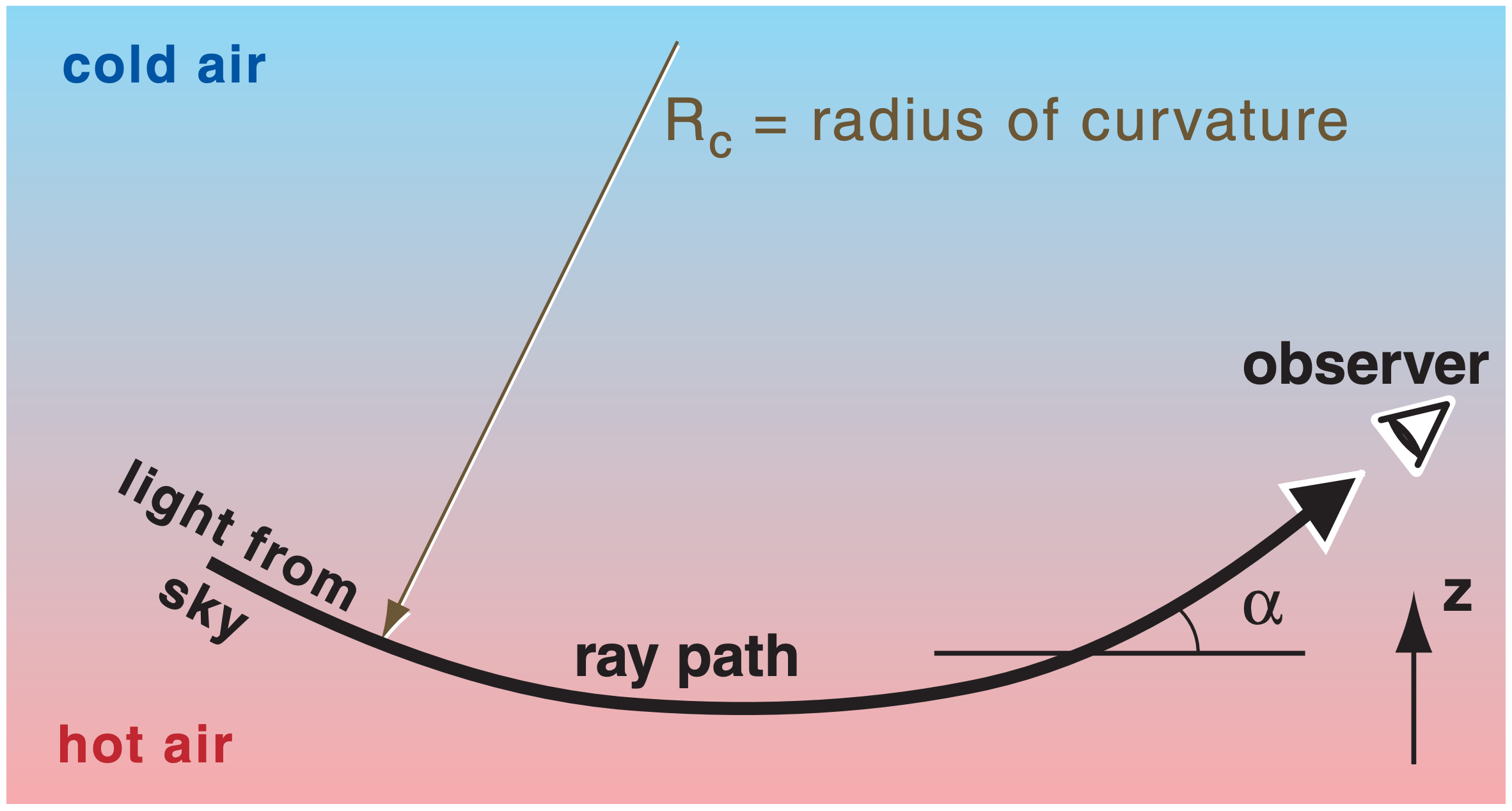
A sharp change in density between two media causes a sharp kink in the ray path (Fig. 22.1). A gradual change of density causes a smoothly curving ray path (Fig. 22.52). The radius of curvature Rc (positive for concave up) is:
\begin{align}R_{c} \approx \frac{\rho_{r e f}}{\left(n_{r e f}-1\right) \cdot(\cos \alpha) \cdot(\Delta \rho / \Delta z)}\tag{22.26}\end{align}
where α is the angle of the ray above horizontal, and the gradient of density ∆ρ/∆z is assumed to be perpendicular to the Earth’s surface.
Substituting the ideal gas law and the hydrostatic relationship from Chapter 1 into eq. (22.26) yields:
\begin{align}R_{c} \approx \frac{-\left(T / T_{\text {ref}}\right) \cdot\left(P_{\text {ref}} / P\right)}{\left(n_{\text {ref}}-1\right) \cdot(\cos \alpha) \cdot\left\{\frac{1}{T}\left[\frac{\Delta T}{\Delta z}+a\right]\right\}}\tag{22.27}\end{align}
where a = 0.0342 K·m–1.
Because average density decreases with height in the atmosphere (see Chapter 1), eq. (22.27) gives a negative radius of curvature in the presence of weak temperature gradients. In other words, the ray is bent downward in a standard atmosphere. This agrees with Huygens’ principle, that says light rays are bent toward media of higher density.
Sample Application
What is the radius of curvature of a horizontal indigo (λ ≈ 0.45 µm from Table 2-3 in the Radiation chapter) ray near the ground in a standard atmosphere?
Find the Answer
Given: z = 0, α = 0°, nair ≈ 1.00028 from Table 22-1 for indigo light.
Find: Rc = ? km
Assume T = 288K and P = 101.3 kPa in a standard atmosphere near the ground. Assume the vertical temperature gradient is negligible. Rearrange eq. (22.27):
R_{c} \approx \frac{-1}{(0.00028) \cdot\left(\cos 0^{\circ}\right) \cdot\left(0.0342 \mathrm{K} \cdot \mathrm{m}^{-1} / 288 \mathrm{K}\right)}
=\underline{\bf{-30,000 \mathrm{km}}}
Check: Units OK. Physics OK.
Exposition: The large negative radius implies very weak downward curvature, which agrees with the small angle of the apparent sunrise (Table 2-2).
For ray paths near horizontal, the total bending through the whole atmosphere is about 0.567°, which is why apparent sunrise occurs before geometric sunrise (see the Radiation chapter). In everyday life, we rarely notice refraction associated with the standard atmosphere. However, in the presence of strong temperature gradients we can see mirages.
For rays to bend up instead of down, the term in square brackets in eq. (22.27) must be negative. This is possible when ∆T/∆z < –a. A temperature decrease of at least 3.5°C per 10 cm height rise is necessary. Such a strong gradient is possible on hot sunny days in the air touching strongly-absorbing (black) surfaces. This condition of warm air under cold causes inferior mirages, where the objects appear lower than they really are. Warm under cold air is statically unstable (see the Atmospheric Stability chapter), causing turbulence that makes these mirages shimmer.
Inferior mirages are common above black roads on hot sunny days. Looking down toward the road, you see light rays refracted from the sky (Fig. 22.52). As these shimmer in the convective turbulence, the mirages look similar to reflections from the surface of water puddles.
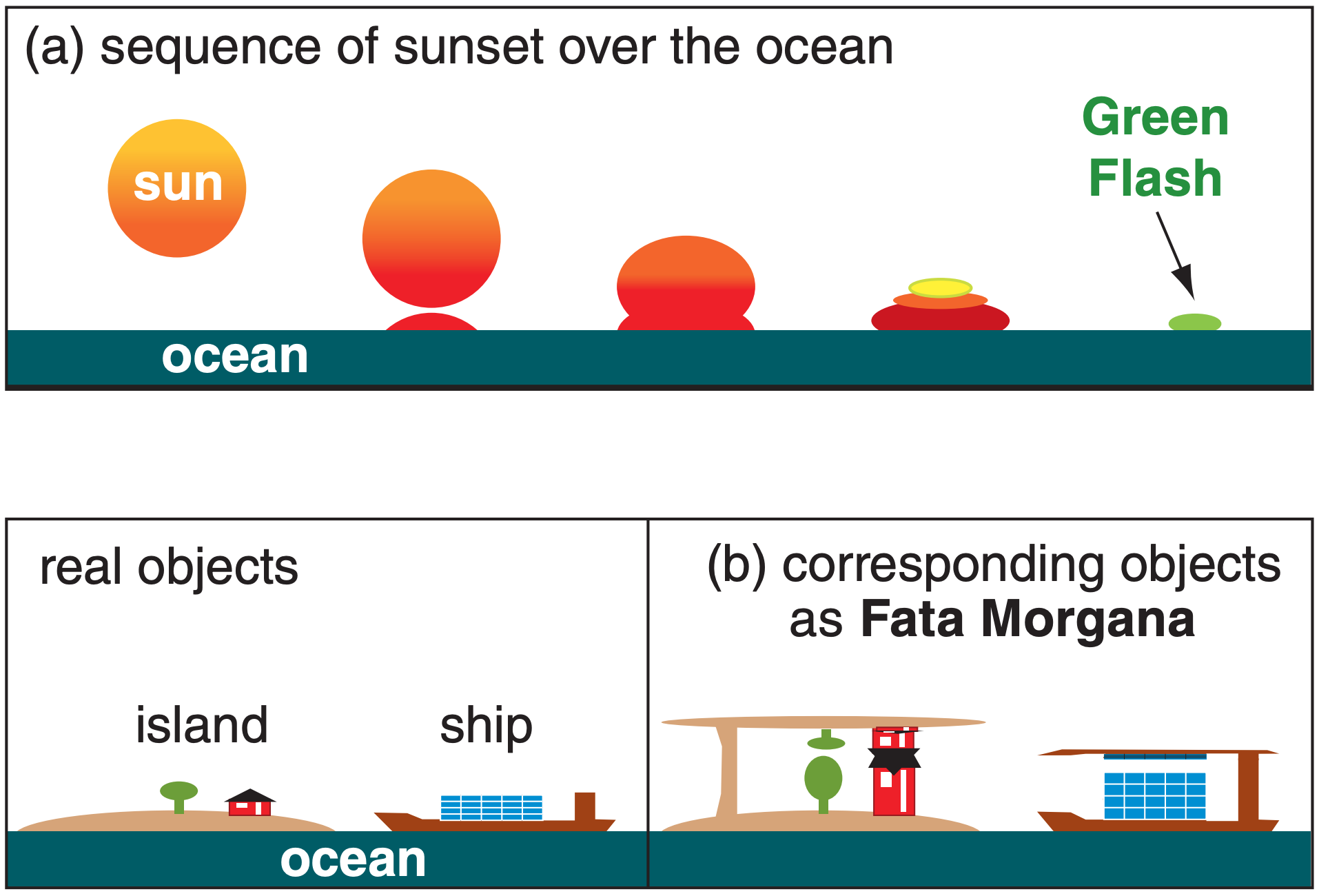
Inferior mirages can also form over the ocean, if a thin layer of warm air is created by heat conduction from a warm sea surface, but colder air exists aloft. As the sun sets over the ocean, the base of the sun sometimes appears to spread out (Fig. 22.53a), causing the shape of the sun’s outline to look like the Greek letter omega (Ω). Later, just as the top of the sun sets, the inferior-mirage effect causes the top of the sun to briefly appear emerald green just before it disappears below the horizon. This phenomenon is called green flash. [CAUTION: to avoid damaging your eyes, do not look directly at the sun.]
Cold air under warm air (as during early morning over land, or in arctic regions over ice, or where warm air flows over cold seas) causes superior mirages, where objects appear higher than they are. This accentuates the downward bending of rays, causing the image of the object to loom or stretch vertically upward.
The Fata Morgana mirage is caused by light rays passing through one or more elevated temperature inversions (a sharp interface between cold air below and warmer air aloft). Some ray paths bend as in superior mirages, and others bend as in inferior mirages. This causes portions of normal objects to appear stretched in the vertical, and other portions to appear compressed (Fig. 22.53b) or flipped.
The results are fanciful images of mountains, ramparts, and castle turrets (some of which appear to float above ground) where none exist in reality.
The name of this mirage comes from Fairy Morgan (or Fata Morgana in Italian) of the King Arthur legend, an enchantress/magician who could create illusions of floating castles, etc.
To confirm his laws of motion, Isaac Newton wanted to view the motions of the planets. He built his own telescopes for this purpose. However, the images he observed through his lenses were blurry. For example, images of stars were spread (dispersed) into a streak of colors.
After experimenting with different lenses, he concluded that neither the glass nor the construction was flawed. He realized that there must be some unknown physics causing this optical phenomenon. Like many great scientists, he allowed himself to get side-tracked to study this phenomenon in detail.
One of his experiments was to obtain a triangular prism, and to allow sunlight to pass through it. He observed that the white sunlight is composed of a spectrum of colors: red, orange, yellow, green, blue, indigo, and violet. Newton must have had a unique sense of color, because most people cannot discriminate between indigo and violet in the spectrum.
Newton concluded that the refraction of light through a lens inevitably causes color dispersion. Thus, a pinpoint of white starlight would be spread into a smear of colors. His solution to the telescope problem was to design a telescope without glass lenses. Instead he invented a reflecting telescope using curved mirrors, because reflection does not cause separation of light into colors.


