22.4: Scattering
- Page ID
- 10197
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)22.4.1. Background
22.4.1.1. Optical thickness
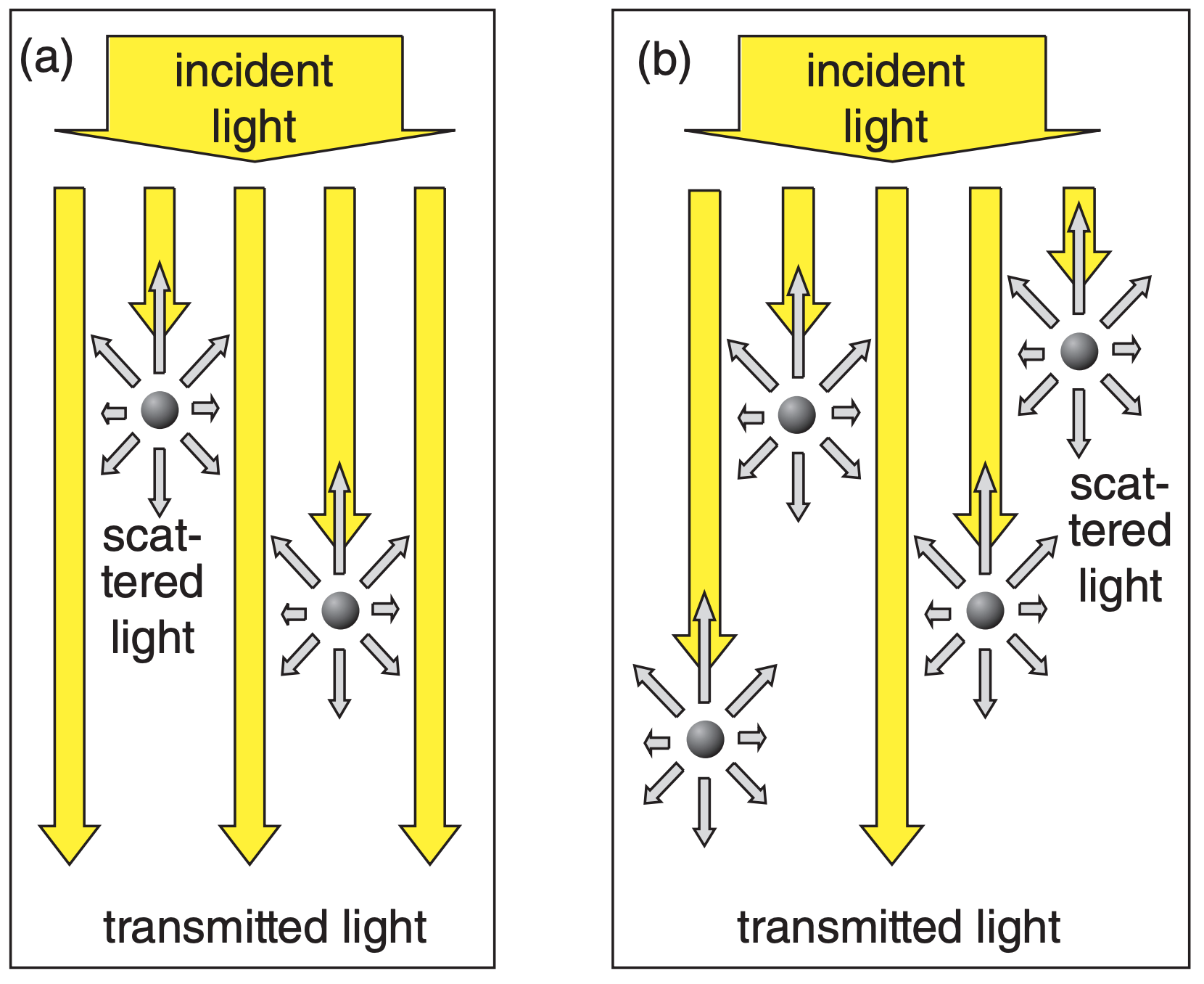
Light can scatter off of air molecules, pollutant particles, dust, and cloud droplets. More particles in the air cause more of the light to be scattered (Fig. 22.42). The ratio of transmitted (Itran , non-scattered) to incident (Io) light can be quantified using the optical thickness or optical depth \(\ \tau\) (dimensionless) in Beer’s Law:
\begin{align}\dfrac{I_{t r a n}}{I_{o}}=e^{-\tau}\tag{22.20}\end{align}
Thus, the relative amount of light scattered (Iscat) is:
\begin{align}\dfrac{I_{\text {scat}}}{I_{o}}=1-\dfrac{I_{\text {tran}}}{I_{o}}=1-e^{-\tau}\tag{22.21}\end{align}
Zero optical thickness means no light is scattered, while \(\ \tau\) > 5 implies that virtually all the light is scattered. Optical thickness increases for longer paths and for higher particle concentrations. Examples are \(\ \tau\) = 0.03 to 0.3 for a clean dry atmosphere, and \(\ \tau\) > 10 for thick clouds.
Sample Application
What fraction of light is scattered for \(\ \tau\) = 2 ?
Find the Answer
Given: \(\ \tau\) = 2
Find: Iscat/Io = ?
Use eq. (22.21): Iscat/Io = 1 –e–2 = 0.865 = 86.5%
Check: Units OK. Magnitudes agree with text.
Exposition: A large portion of light is scattered. This optical depth can occur in polluted air.
22.4.1.2. Polarization
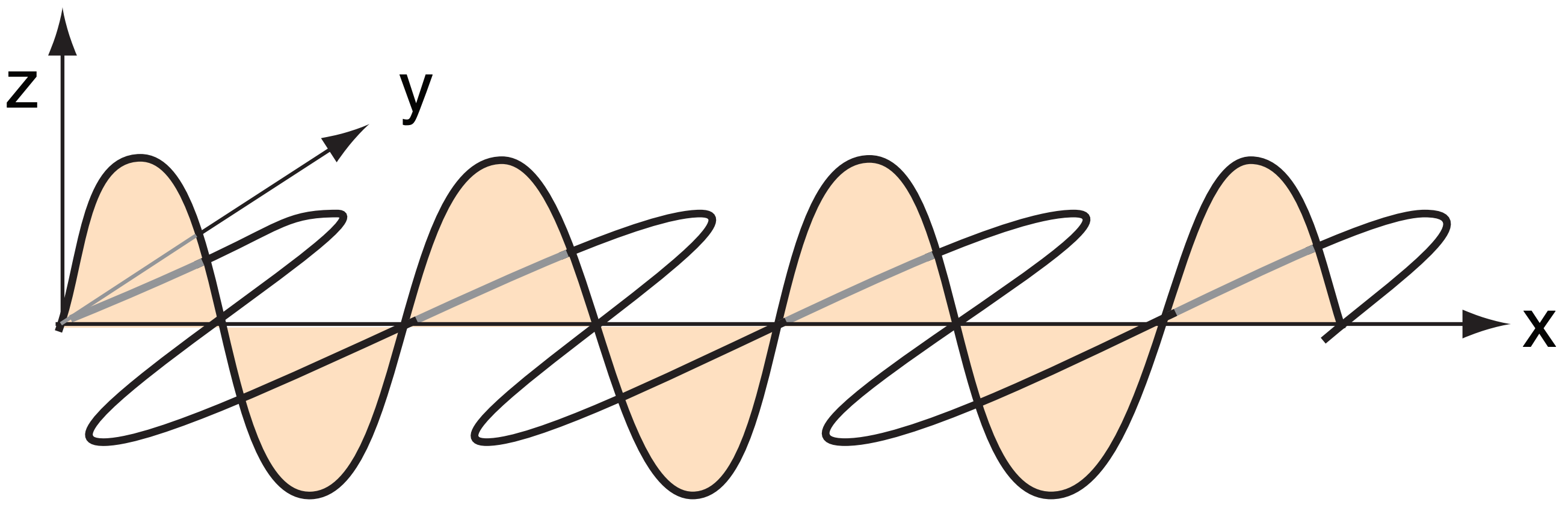
Light propagating in the x-direction can be thought of as having oscillations in the y and z directions (Fig. 22.43). This is unpolarized light. Polarizing filters eliminate the oscillations in one direction (for example, the shaded curve) while allowing the other oscillations to pass through. What remains is polarized light, which has half the intensity of the unpolarized ray.
Sunlight becomes polarized when it is scattered from air molecules. The maximum amount of polarization occurs along an arc in the sky that is 90° from the sun, as viewed from the ground (Fig. 22.44).
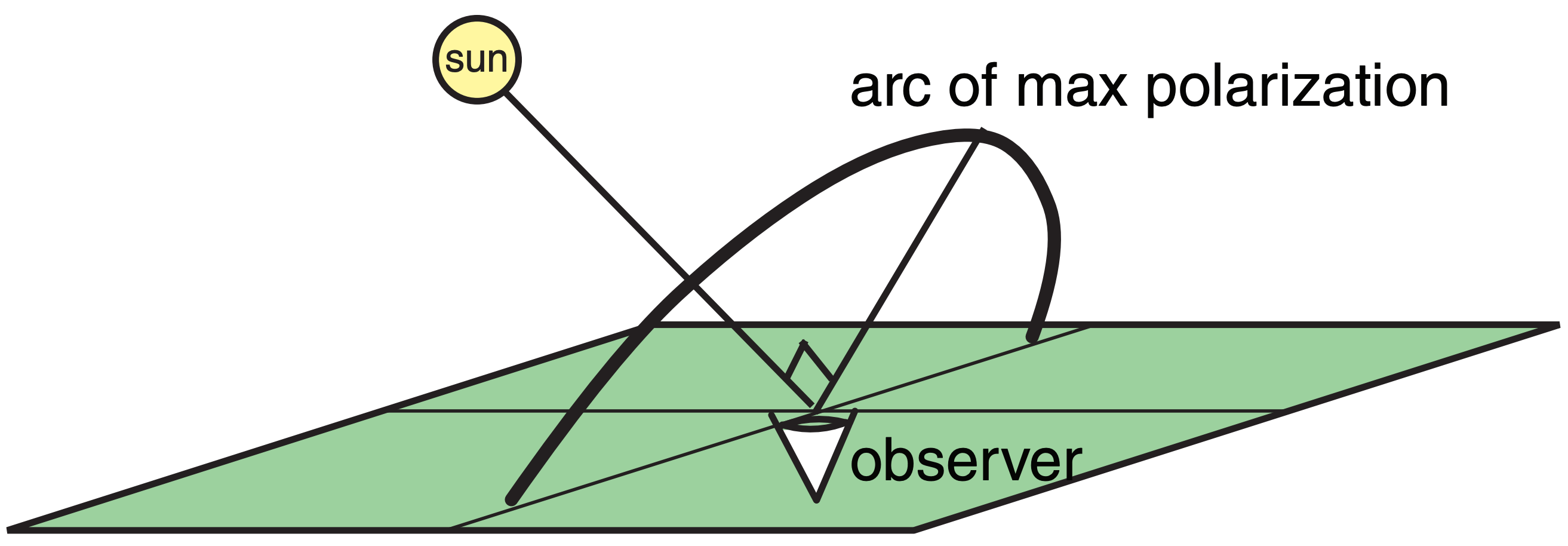
If the sky scatters light with one polarity, and a polarizing camera filter or polarized sunglasses are rotated to eliminate it, then virtually no sky light reaches the camera or observer. This makes the sky look very deep blue, providing a very striking background in photographs of clouds or other objects. If you want to maximize this effect, pick a camera angle looking toward the 90° arc from the sun.
22.4.1.3. Types of Scattering
The type and efficiency of scattering depends on the ratio of particle diameter D to the wavelength λ of the light. Table 22-4 summarizes the types of scattering. Actual size ranges of cloud droplets and aerosols are wider than indicated in this table.
|
Table 22-4. Scattering of visible light. D = particle diameter. λ = wavelength of light. |
Scattering Varies with | ||||||
|---|---|---|---|---|---|---|---|
| D / λ | Particles | Diameter, D (µm) | Type | Phenomena | λ | Direction | Polarization |
| < 1 | air molecules | 0.0001 to 0.001 | Rayleigh | blue sky, red sunsets | X | X | |
| ≈ 1 | aerosols (smog) | 0.01 to 1.0 | Mie | brown smog | X | X | X |
| > 1 | cloud droplets | 10 to 100 | geometric | white clouds | X | ||
22.4.2. Rayleigh Scattering
Air molecules have sizes of D ≈ 0.0001 to 0.001 µm, which are much smaller than the wavelength of light (λ = 0.4 to 0.7 µm). These particles cause Rayleigh scattering. The ratio of scattered intensity of radiation Iscat to the incident radiation intensity Io is:
\begin{align}\dfrac{I_{\text {scat}}}{I_{o}} \approx 1-\exp \left[-\dfrac{a \cdot\left(n_{\text {air}}-1\right)^{2}}{\rho \cdot \lambda^{4}} \cdot x\right]\tag{22.22}\end{align}
where a = 1.59x10–23 kg, ρ is air density, nair is the refractive index, and x is the path length of light through the air.
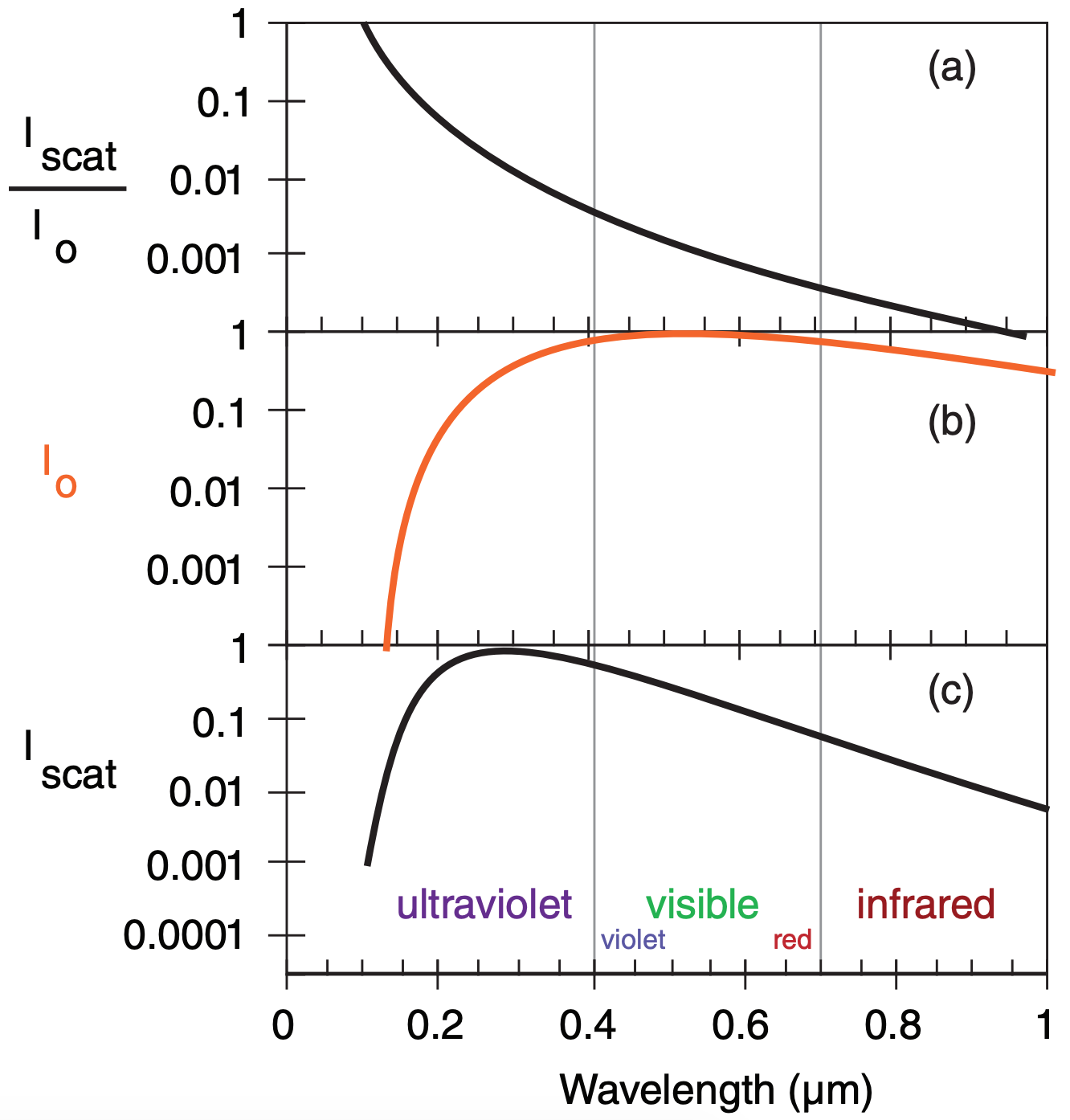
Fig. 22.45a shows the relative amount of scattering vs. wavelength. Because of the λ–4 dependence, shorter wavelengths such as blue and violet are scattered much more (about a factor of 10) than red light, which causes our blue sky color. For light shining vertically through a clean dry atmosphere, \(\ \tau\) = 0.3 for violet light and 0.03 for red.
Sunlight intensity varies according to Planck’s law (Fig. 22.45b and the Solar & Infrared Radiation chapter). The product of the top 2 curves shows the amount of sunlight that is scattered in the atmosphere (Fig. 22.45c). All curves have been normalized to have a maximum of 1.0.
The curve in Fig. 22.45c peaks in the ultraviolet portion of the spectrum. Although this is not visible to the naked eye, the scattered ultraviolet light can affect photographic films to produce a picture that looks hazier than the view by eye. Haze filters on cameras can filter out this unwanted scattered ultraviolet light.
Sample Application
What fraction of incident violet light is scattered by air molecules along a 20 km horizontal ray path near the Earth?
Find the Answer
Given: x = 5x106 m, λ = 4x10–7 m for violet
Find: Iscat/Io = ?
Assume: ρ = 1 kg·m–3 for simplicity
Use eq. (22.22): Iscat/Io =
\(\ 1-\exp \left[-\dfrac{\left(1.59 \times 10^{-23} \mathrm{kg}\right) \cdot(0.0002817)^{2}}{\left(1 \mathrm{kg} \cdot \mathrm{m}^{-3}\right) \cdot\left(4 \times 10^{-7} \mathrm{m}\right)^{4}} \cdot\left(2 \times 10^{4} \mathrm{m}\right)\right]
=\underline{\bf{0.627}}=62.7 \% \text { scattered }\)
Check: Units OK. Physics OK.
Exposition: Looking toward the horizon, distant objects are difficult to see because some of the light is lost. Vertical rays experience less scattering, because air density decreases with height.
22.4.4. Mie Scattering
Gustov Mie proposed a comprehensive theory that describes reflection, scattering, polarization, absorption, and other processes for particles of all sizes. The theory reduces to Rayleigh scattering for particles smaller than the wavelength of light, and to geometric scattering for larger particles. Aerosol particles have an intermediate size, so no simplification of Mie theory is possible.
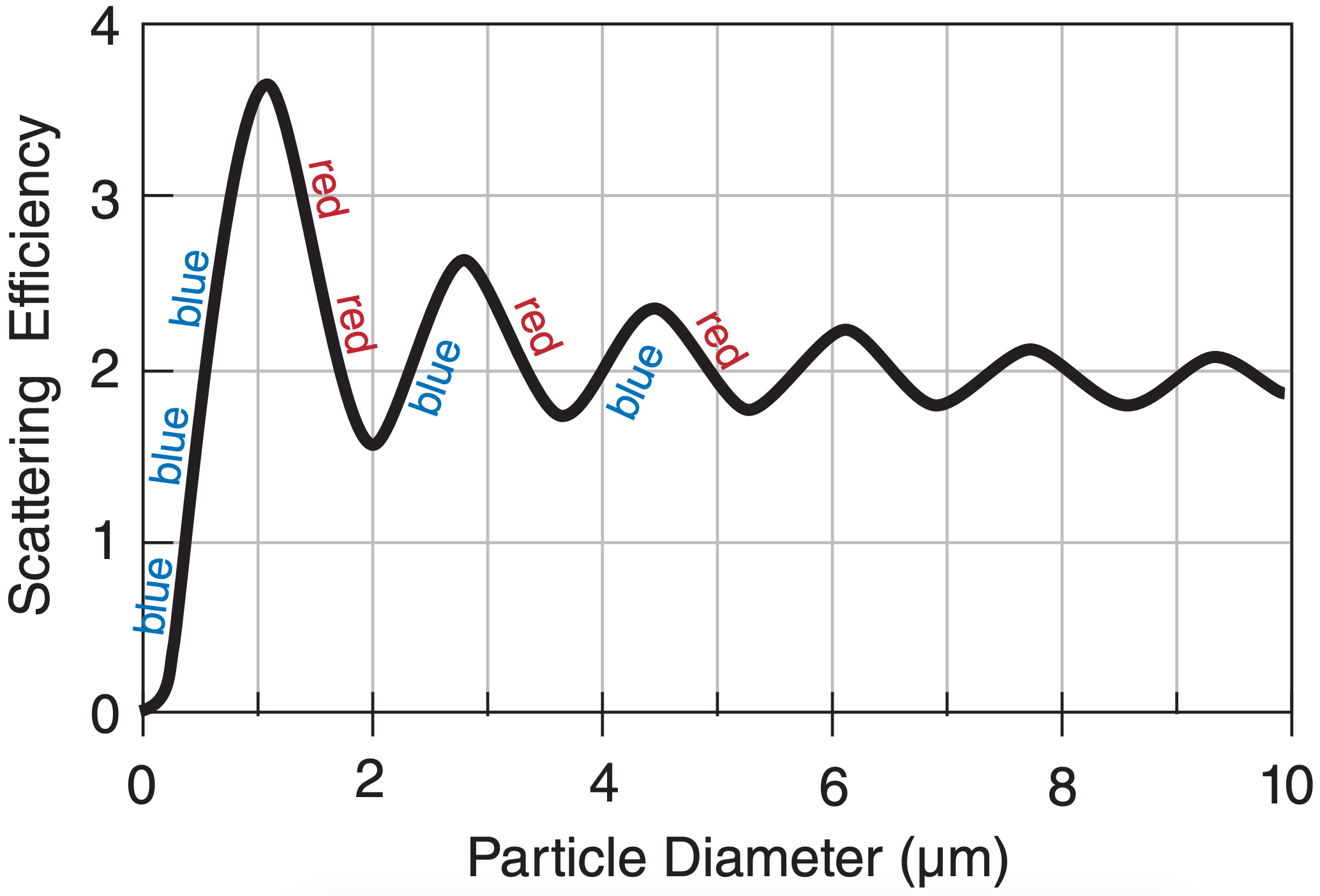
Fig. 22.46 shows that aerosols with diameters greater than about 0.1 µm are 10 to 1000 times more efficient light scatterers than air molecules, which is why polluted air looks hazy and has low visibility. Uniform aerosol smog particles can produce bluish or reddish-brown colors, depending on the dominant aerosol diameter.
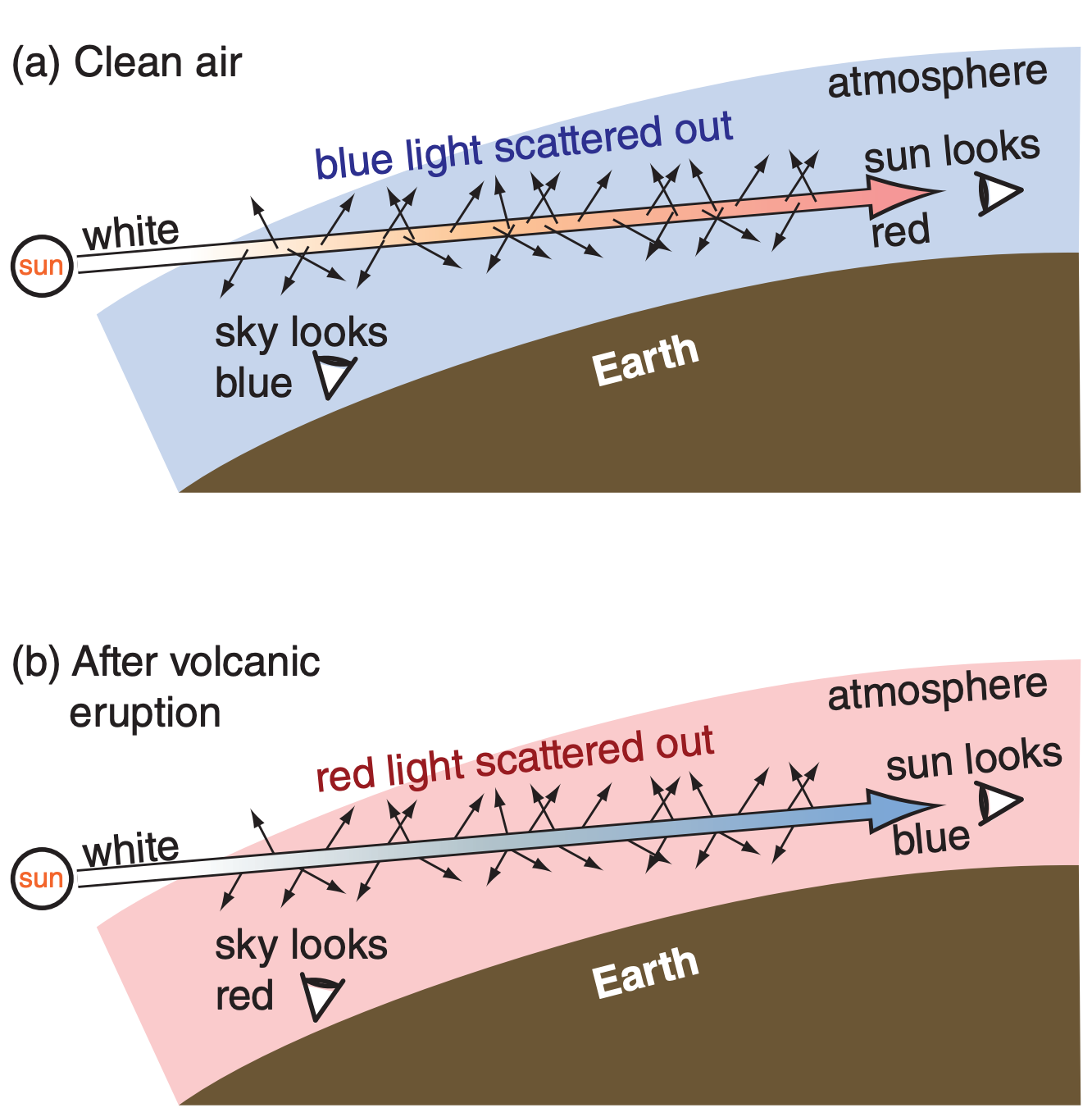
Most aerosol particles have diameters smaller than 1 µm. Fig. 22.46 shows that these aerosols still scatter more blue light than red, causing blue haze. When the sun is low in the sky, the light rays travel through a very long path of air en route to the observer. For this situation, so much blue light is scattered out (making our blue sky) by these small aerosols and air molecules that it leaves more red in the remaining direct beam — giving a beautiful red sun at sunrise or sunset (Fig. 22.47a).
However, some acid droplet aerosols have diameters of about 1.5 µm, which scatters more red than blue. In some polluted regions where combustion processes emit SO2 and NO2 into the air, these pollutants can react with water in the air to form sulfuric acid and nitric acid. Scattering in this condition creates a brown cloud haze.
Another source of 1.5 µm diameter acid aerosols is volcanic eruptions, where sulfur emissions change into sulfuric acid droplets in the stratosphere. When the sun is low in the sky, so much red light is scattered out that beautiful crimson sunset skies are often observed after volcanic eruptions (Fig. 22.47b). Also, this leaves the remaining direct beam of sunlight in the setting sun slightly blue, which is hard to see because it is so bright. However, direct moonlight from a rising or setting moon can often be blue — causing a blue moon after a volcanic eruption.
For aerosols, forward scattering is usually greater than backscattering. Scattering can be polarized.


