17.9: Bernoulli's Equation
- Page ID
- 10597
17.9.1. Principles
Consider a steady-state flow (flow that does not change with time), but which can have different velocities at different locations. If we follow an air parcel as it flows along a streamline, its velocity can change as it moves from one location to another. For wind speeds M ≤ 20 m s–1 at constant altitude, the air behaves as if it is nearly incompressible (namely, constant density ρ).
17.9.1.1. Incompressible Flow
For the special case of incompressible, steadystate, laminar (non-turbulent) motion with no drag, the equations of motion for an air parcel following a streamline can be simplified into a form known as Bernoulli’s equation:
\( \begin{align} \frac{1}{2} M^{2}+\frac{P}{\rho}+|g| \cdot z=C_{B}\tag{17.35}\end{align}\)
\(\ energy: kinetic + flow + potential = constant\)
where M is the total velocity along the streamline, P is static air pressure, ρ is air density, |g| = 9.8 m·s–2 is gravitation acceleration magnitude, and z is height above some reference.
Sample Application
Environmental air outside a hurricane has sea-level pressure 100 kPa. Find the rise in sea level at the eye, where sea-level pressure is 90 kPa. Neglect currents and wind waves.
Find the Answer
Given: Penv = 100 kPa, zenv = 0 m, Peye = 90 kPa, M≈ 0
Find: zeye = ? m , where z is height of sea level.
Consider a streamline in the water at the sea surface. ρ = 1025 kg m–3 for sea water.
Use Bernoulli’s eq. (17.35) to find CB for the environment, then use it for the eye:
Env: 0.5·(0m s–1)2 + (100,000Pa)/(1025kg m–3) + (9.8 m s–2)·(0m) = CB = 97.6 m2 s–2
Eye: 0.5·(0m s–1)2 + (90,000Pa)/(1025kg m–3) + (9.8 m s–2)·(zeye) = CB = 97.6 m2 s–2
zeye = {(97.6 m2 s–1)–[(90,000Pa)/(1025kg m–3)]}/ (9.8 m s–2) = 1.0 m.
Check: Units OK. Magnitude OK.
Exposition: Such a rise in sea level is a hazard called the storm-surge.
CB is an arbitrary constant called Bernoulli’s constant or Bernoulli’s function. CB is constant along any one streamline, but different streamlines can have different CB values.
Bernoulli’s equation focuses on mechanical-energy conservation along a streamline. The first term on the left is the kinetic energy per unit mass. The middle term is the work done on the air (sometimes called flow energy per unit mass) that has been stored as pressure. The last term on the left is the potential energy per unit mass. Along any one streamline, energy can be converted from one form to another, provided the sum of these energies is constant.
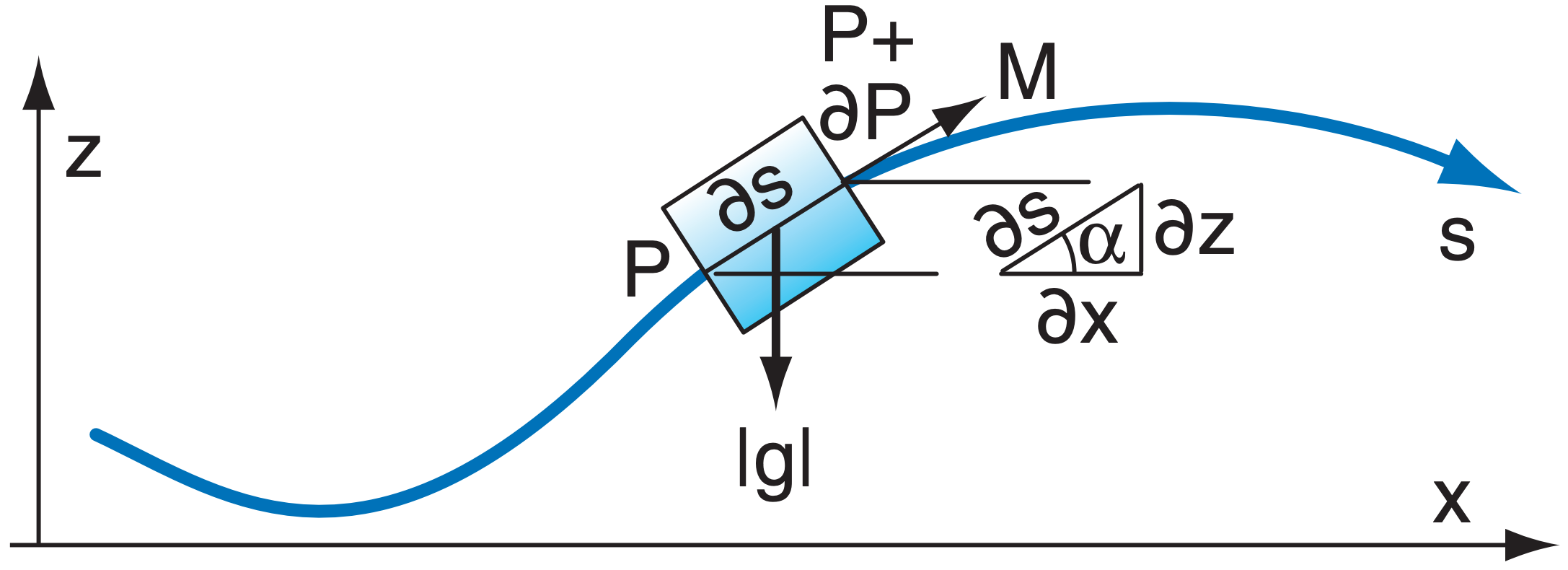
To derive Bernoulli’s equation, apply Newton’s second law (a = F/m) along a streamline s. Acceleration is the total derivative of wind speed: a = dM/dt = ∂M/∂t + M·∂M/∂s. Consider the special case of flow that is steady at any location (∂M/∂t = 0) even though the flow can be different at different locations (∂M/∂s ≠ 0). Thus
\(\ M \cdot \partial M / \partial s=F / m\)
The forces per unit mass F/m acting on a fluid parcel along the direction of the streamline are pressuregradient force and the component of gravity along the streamline [ |g|·sin(α) = |g|·∂z/∂s ]:
\(\ M \cdot \partial M / \partial s=-(1 / \rho) \cdot \partial P / \partial s-|g| \cdot \partial z / \partial s\)
or
\(\ (1/2) dM^2 + (1/ρ)·dP + |g|·dz = 0\)
For incompressible flow, ρ = constant. Integrate the equation above to get Bernoulli’s equation:
\(\ (1 / 2) M^{2}+P / \rho+|g| \cdot z=C_{B}\)
where CB is the constant of integration.
This result applies only to steady incompressible flow along a streamline. Do not use it for situations where additional forces are important, such as turbulent drag, or across wind turbines or fans.
In hydraulics, the gravity term is given by the change in depth of the water, especially when considering a streamline along the water surface. In meteorology, a similar situation occurs when cold air rises into a warmer environment; namely, it is a dense fluid rising against gravity. However, the gravity force felt by the rising cold air is reduced because of its buoyancy within the surrounding air. To compensate for this, the gravity factor in Bernoulli’s equation can be replaced with a reduced gravity g’ = |g|·∆θv/Tv , yielding:
\( \begin{align} \frac{1}{2} M^{2}+\frac{P}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.36}\end{align}\)
where ∆θv is the virtual potential temperature difference between the warm air aloft and the cold air below, and Tv is absolute virtual air temperature (K). Thus, the gravity term is nonzero when the streamline of interest is surrounded by air of different virtual potential temperature, for air flowing up or down.
Sample Application
Cold-air flow speed 10 m s–1 changes to 2 m s–1 after passing a hydraulic jump. This air is 10°C colder than the surroundings. How high can the hydraulicjump jump?
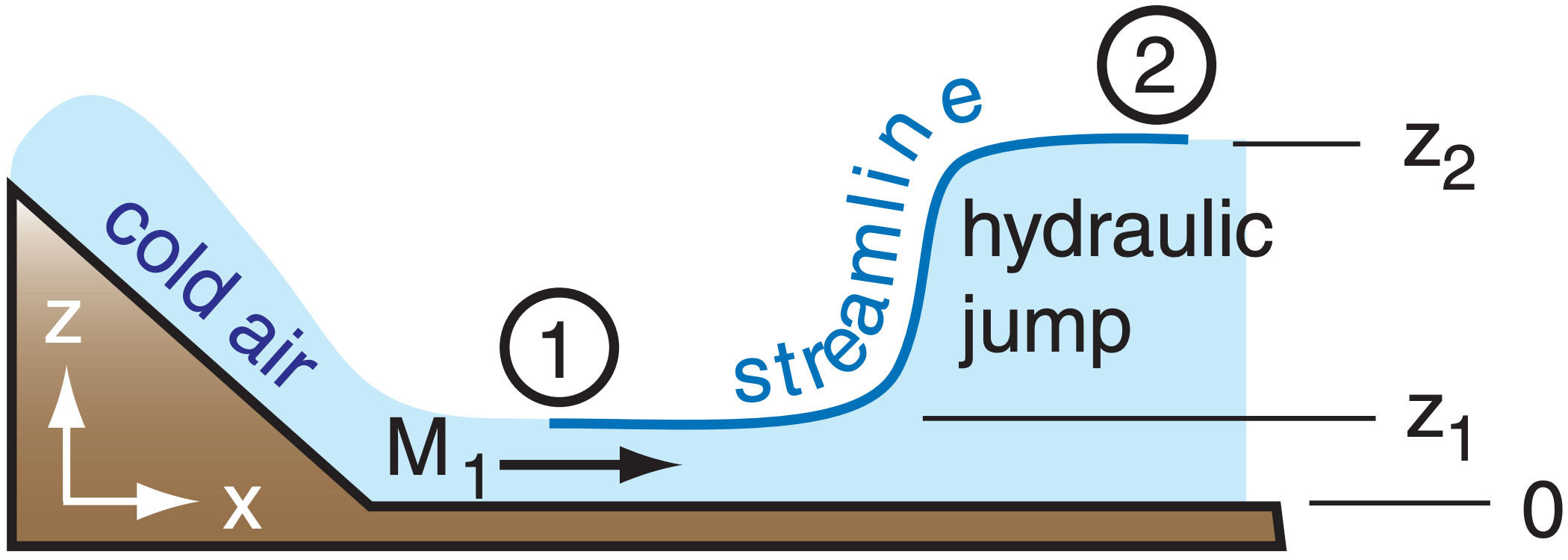
Find the Answer
Given: M1 = 10 m s–1, M2 = 2 m s–1, ∆T = 10K, z1 = 0.
Find: z2 = ? m above the initial z.
Assume: ∆θv = ∆T and |g|/Tv = 0.0333 m·s–2·K–1. P ≈ constant on a streamline along the top of the cold air.
Use eq. (17.36), noting that CB – P/ρ is constant :
- At point 1: 0.5 ·(10m s–1)2 + 0 = CB – P/ρ = 50 m2 s–2
- At 2: 0.5·(2m s–1)2+(0.0333m·s–2·K–1)·(10K)·z2 =50 m2 s–2
Solve for z2: z2 = [M12 – M22] ·Tv/(2·|g|·∆θv) = 144 m
Check: Units OK. Magnitude OK.
Exposition: Hydraulic jumps are very turbulent and would dissipate some of the mechanical energy into heat. So the actual jump height would be less.
To use eq. (17.36), first measure all the terms in the left side of the equation at some initial (or upstream) location in the flow. Call this point 1. Use this to calculate the initial value of CB. Then, at some downstream location (point 2) along the same streamline use eq. (17.36) again, but with the known value of CB from point 1. The following equation is an expression of this procedure of equating final to initial flow states:
\(\ \begin{align} \frac{1}{2} M_{2}^{2}+\frac{P_{2}}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z_{2}=\frac{1}{2} M_{1}^{2}+\frac{P_{1}}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z_{1}\tag{17.37}\end{align}\)
Another way to consider eq. (17.36) is if any one or two terms increase in the equation, the other term(s) must decrease so that the sum remains constant. In other words, the sum of changes of all the terms must equal zero:
\(\ \begin{align} \Delta\left[\frac{1}{2} M^{2}\right]+\Delta\left[\frac{P}{\rho}\right]+\Delta\left[|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot z\right]=0\tag{17.38}\end{align}\)
Caution: ∆[(0.5)·M2] ≠ (0.5)·[∆M]2.
The Bernoulli equations above do NOT work:
- anywhere that the flow is turbulent
- behind obstacles that create turbulent wakes or that cause sudden changes in the flow
- at locations of heat input or loss
- at locations of mechanical-energy input (such as a fan) or loss (such as a wind turbine)
- near the ground where drag slows the wind
- where flow speed > 20 m s–1
- where density is not approximately constant
Hence, there are many atmospheric situations for which the above equations are too simplistic.
Sample Application
Wind at constant altitude decelerates from 15 to 10 m s–1 while passing through a wind turbine. What opposing net pressure difference would have caused the same deceleration in laminar flow?
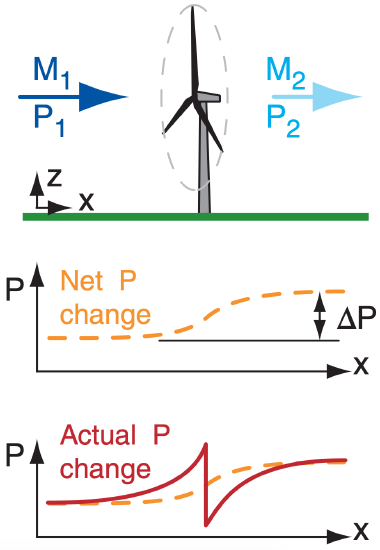 Find the Answer
Find the Answer
Given: ∆z = 0, M1 = 15 m s–1 , M2 = 10 m s–1.
Find: ∆P = ? Pa
Assume ρ = 1 kg m–3 = constant.
Solve eq. (17.38) for ∆P: ∆P = – ρ · ∆[(0.5)·M2]
∆P = – (1 kg m–3) · (0.5)·[(10m s–1)2 – (15m s–1)2] = 62.4 Pa
Check: Units OK. Magnitude OK.
Exposition: The process of extracting mechanical energy from the wind has the same affect as an opposing pressure difference. This pressure difference is small compared to ambient atmospheric pressure P = 100,000 Pa.
The actual pressure change across a wind turbine is shown in bottom figure.
17.9.1.2. Compressible Flow
For many real atmospheric conditions where winds can be any speed, you should use a more general form of the Bernoulli equation that includes thermal processes.
For an isothermal process, the equation becomes:
\(\ \begin{align} \frac{1}{2} M^{2}+\mathfrak{R}_{d} \cdot T_{v} \cdot \ln (P)+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.39}\end{align}\)
where ℜd = 287 m2·s–2·K–1 is the ideal gas constant for dry air, and where CB is constant during the process (i.e., initial CB = final CB).
Sample Application
Air with pressure 100 kPa is initially at rest. It is accelerated over a flat 0°C snow surface as it is sucked toward a house hold ventilation system. If the final speed is 10 m s–1, what is the air pressure at the fan entrance?
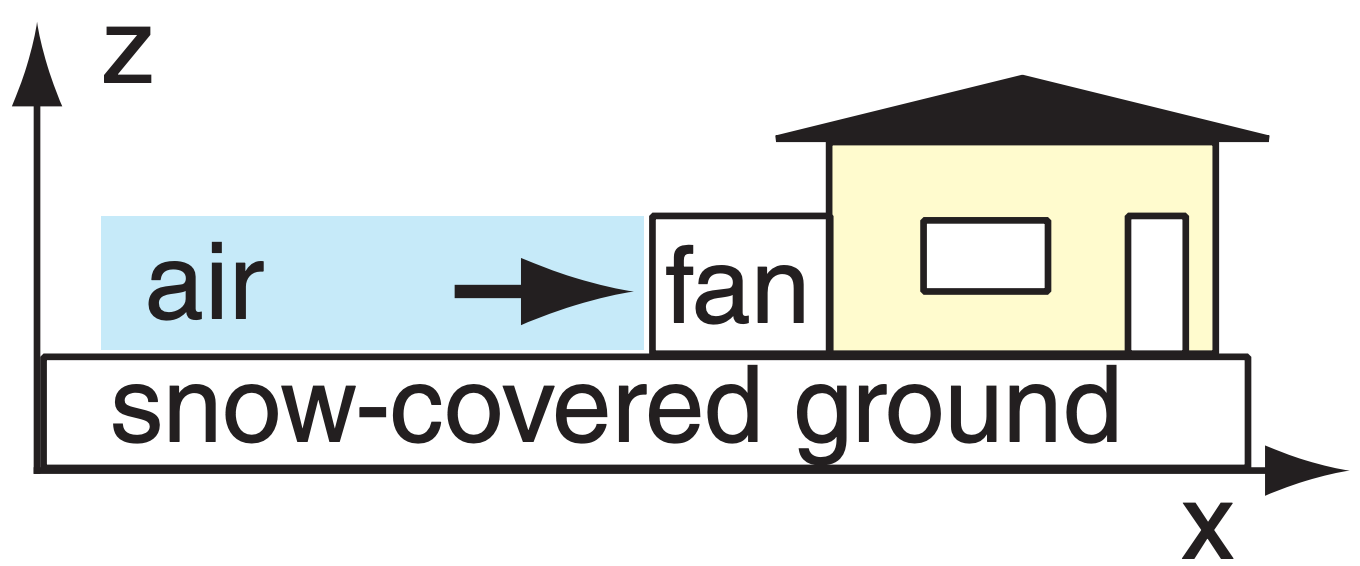
Find the Answer
Given: P1 = 100 kPa, M1 = 0, M2 = 10 m s–1, ∆z = 0 .
Find: P2 = ? kPa
Assume the snow keeps their air at constant Tv = 0°C. Use eq. (17.39) for an isothermal process:
[0.5M22 – 0] + ℜd·Tv·[ln(P2)–ln(P1)] = 0
Use ln(a) – ln(b) = ln(a/b). Then take exp of both sides, and rearrange: P2 = P1 ·exp[–0.5M22 / (ℜd·Tv)]
P2 = = (100kPa)·exp[–0.5(10m s–1)2/{(287m2·s–2·K–1)·(273K)}] = (100kPa)·exp[–0.000638] = (100kPa)· (0.9994) = 99.94 kPa.
Check: Units OK. Magnitude OK.
Exposition: This decrease of about 0.06 kPa is small compared to ambient P = 100 kPa. The air-pressure decrease is expected because of the suction caused by the fan.
For adiabatic (isentropic; no heat transfer) flow, the Bernoulli equation is
\(\ \begin{align} \frac{1}{2} M^{2}+\left(\frac{C_{p}}{\Re}\right) \frac{P}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.40}\end{align}\)
where Cp is the specific heat at constant pressure, and ℜ is the ideal gas constant. For dry air, Cpd/ℜd = 3.5 (dimensionless).
Using the ideal gas law, this last equation for adiabatic flow along a streamline becomes
\(\ \begin{align} \frac{1}{2} M^{2}+C_{p} \cdot T+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.41}\end{align}\)
kinetic + sensible + potential = constant energy heat
where Cp·T is the enthalpy (also known as the sensible heat in meteorology), and Cp = 1004 m2·s–2·K–1 for dry air. In other words:
\(\ \begin{align} \frac{1}{2} M_{2}^{2}+C_{p} \cdot T_{2}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z_{2}=\frac{1}{2} M_{1}^{2}+C_{p} \cdot T_{1}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z_{1}\tag{17.42}\end{align}\)
where subscript 2 denotes final state, and subscript 1 denotes initial state. Equation (17.41) is also sometimes written as
\(\ \begin{align} \frac{1}{2} M^{2}+C_{v} \cdot T+\frac{P}{\rho}+|g| \frac{\Delta \theta_{v}}{T_{v}} \cdot z=C_{B}\tag{17.43}\end{align}\)
energy: kinetic + internal + flow + potential = constant
Again, CB is constant during the adiabatic process.
Sample Application
A short distance behind the engine of a jet aircraft flying in level flight, the exhaust temperature is 400 °C and the jet-blast speed is 200 m s–1. After the jet exhaust decelerates to zero, what is the final exhaust air temperature, neglecting conduction & turbulent mixing.
Find the Answer
Given: M1 = 200 m s–1, T1 =400°C = 673K, M2 = 0, ∆z=0
Find: T2 = ? °C. Assume adiabatic process.
Rearrange eq. (17.42): T2 = T1 + M12/(2Cp)
T2 = (673K) + (200m s–1)2/(2· 1004 m2·s–2·K–1)
= 673K + 19.9K = 693 K = 420°C
Check: Units OK. Magnitude OK.
Exposition: Jet exhaust is turbulent and mixes quickly with the cooler ambient air, so it is not appropriate to use Bernoulli’s equation. See the “dynamic warming” section later in this chapter for more info.
17.9.1.3. Energy Conservation
Because these several previous equations also consider temperature, we cannot call them Bernoulli equations. They are energy conservation equations that consider mechanical and thermal energies following a streamline.
If we extend this further into an energy budget equation, then we can add the effects of net addition of thermal energy (heat per unit mass) ∆q via radiation, condensation or evaporation, conduction, combustion, etc. We can also include shaft work per unit mass ∆SW done on the air by a fan, or energy extracted from the air by a wind turbine.
\(\ \begin{align} \Delta\left[\frac{1}{2} M^{2}\right]+\Delta\left[\frac{P}{\rho}\right]+\Delta\left[C_{v} \cdot T\right]+\Delta\left[|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot z\right]=\Delta q+\Delta S W\tag{17.44}\end{align}\)
or
\(\ \begin{align} \Delta\left[\frac{1}{2} M^{2}\right]+\Delta\left[C_{p} \cdot T\right]+\Delta\left[|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot z\right]=\Delta q+\Delta S W\tag{17.45}\end{align}\)
Sample Application
A 75 kW electric wind machine with a 2.5 m radius fan is used in an orchard to mix air to reduce frost damage on fruit. The fan horizontally accelerates air from 0 to 5 m s–1. Find the temperature change across the fan, neglecting mixing with environmental air.
Find the Answer
Given: Power = 75 kW = 75000 kg·m2·s–3, R = 2.5 m, M1 = 0, M2 = 5 m s–1, ∆z = 0
Find: ∆T = ? °C
Assume that all the electrical energy used by the fan motor goes into a combination of heat and shaft work.
The mass flow rate through this fan is:
ρ·M2·π·R2 = (1.225kg m–3)·(5m s–1)·π·(2.5m)2 =120 kg s–1
Thus: ∆q + ∆SW = Power/(Mass Flow Rate) = 624 m2·s–2
Use eq. (17.45): ∆T = (1/Cp)·[∆q +∆SW –0.5·(M22 –M12)]
= (1/1004 m2·s–2·K–1)·[(624 m2·s–2) – 0.5·(5m s–1)2]
= 0.61 K = 0.61°C
Check: Units OK. Magnitude OK.
Exposition: In spite of the large energy consumption of the electric motor, the heating is spread into a very large volume of air that passes through the fan. Hence, the amount of temperature change is small.
17.9.2. Some Applications
17.9.2.1. Dynamic & Static Pressure & Temperature
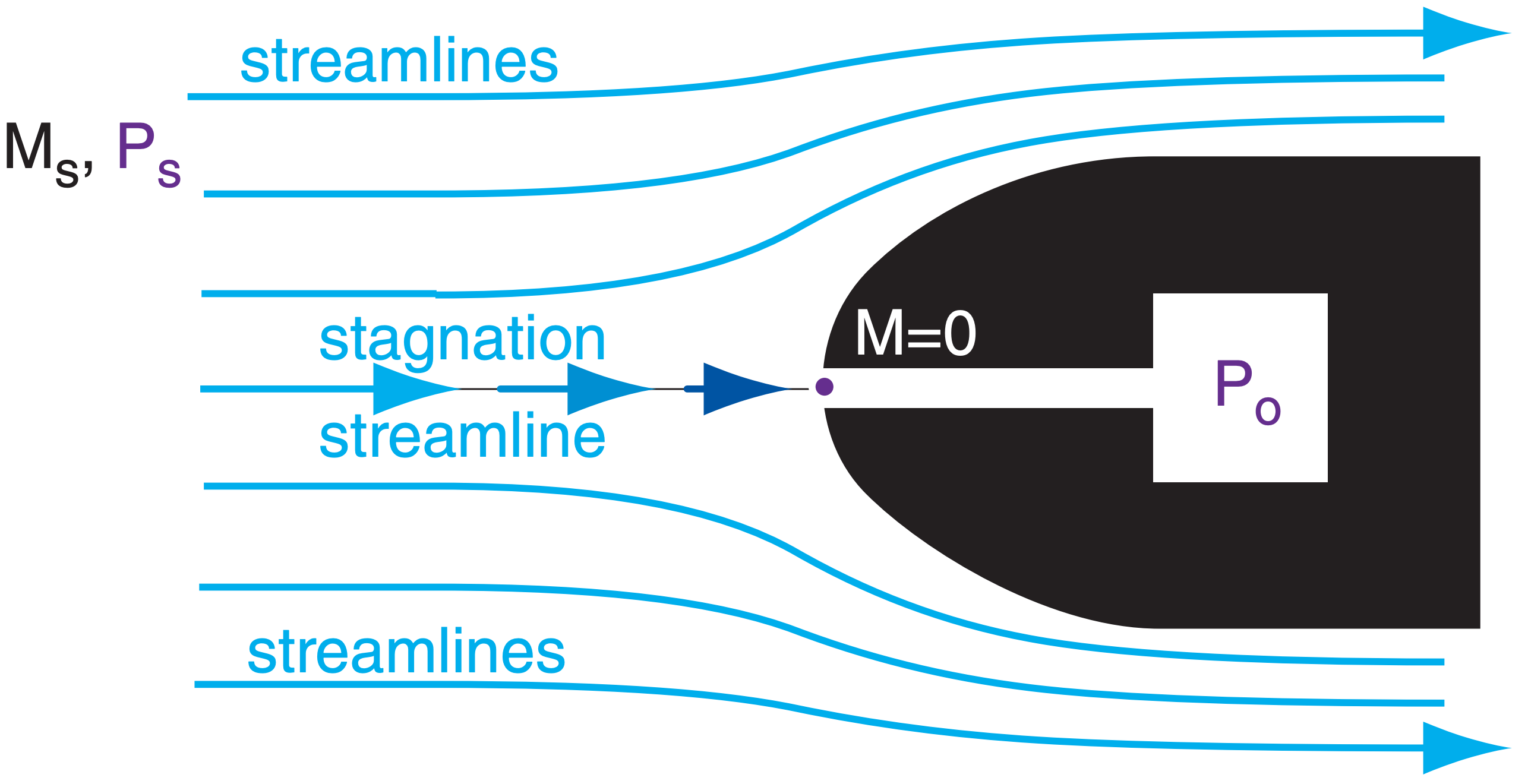
Free-stream atmospheric pressure away from any obstacles is called the static pressure Ps. Similarly, let T be the free stream (initial) temperature.
When the wind approaches an obstacle, much of the air flows around it, as shown in Fig. 17.34. However, for one streamline that hits the obstacle, air decelerates from an upstream speed of Minitial = Ms to an ending speed of Mfinal = 0. This ending point is called the stagnation point.
As air nears the stagnation point, wind speed decreases, and pressure increases as air molecules converge. This causes temperature to increase, according to the ideal gas law. The increased pressure is called the dynamic pressure Pdyn, and the increased temperature is called the dynamic temperature Tdyn. At the stagnation point where velocity is zero, the final dynamic pressure is called the stagnation pressure Po, and the associated dynamic temperature is given the symbol To. Think of subscript “o” as indicating zero wind speed relative to the obstacle.
To find the dynamic effects at stagnation, use the energy conservation equation (17.42) for wind blowing horizontally (i.e., no change in z), and assume a nearly adiabatic process:
\(\ \begin{align} C_{p} \cdot T_{o}=\frac{1}{2} M_{s}^{2}+C_{p} \cdot T\tag{17.46}\end{align}\)
Solving for the dynamic temperature To gives:
\(\ \begin{align} T_{o}=T+\frac{M_{s}^{2}}{2 \cdot C_{p}}\tag{17.47}\end{align}\)
where Cp = 1004 m2·s–2·K–1 for dry air. Eq. (17.47) is valid for subsonic speeds (see INFO box).
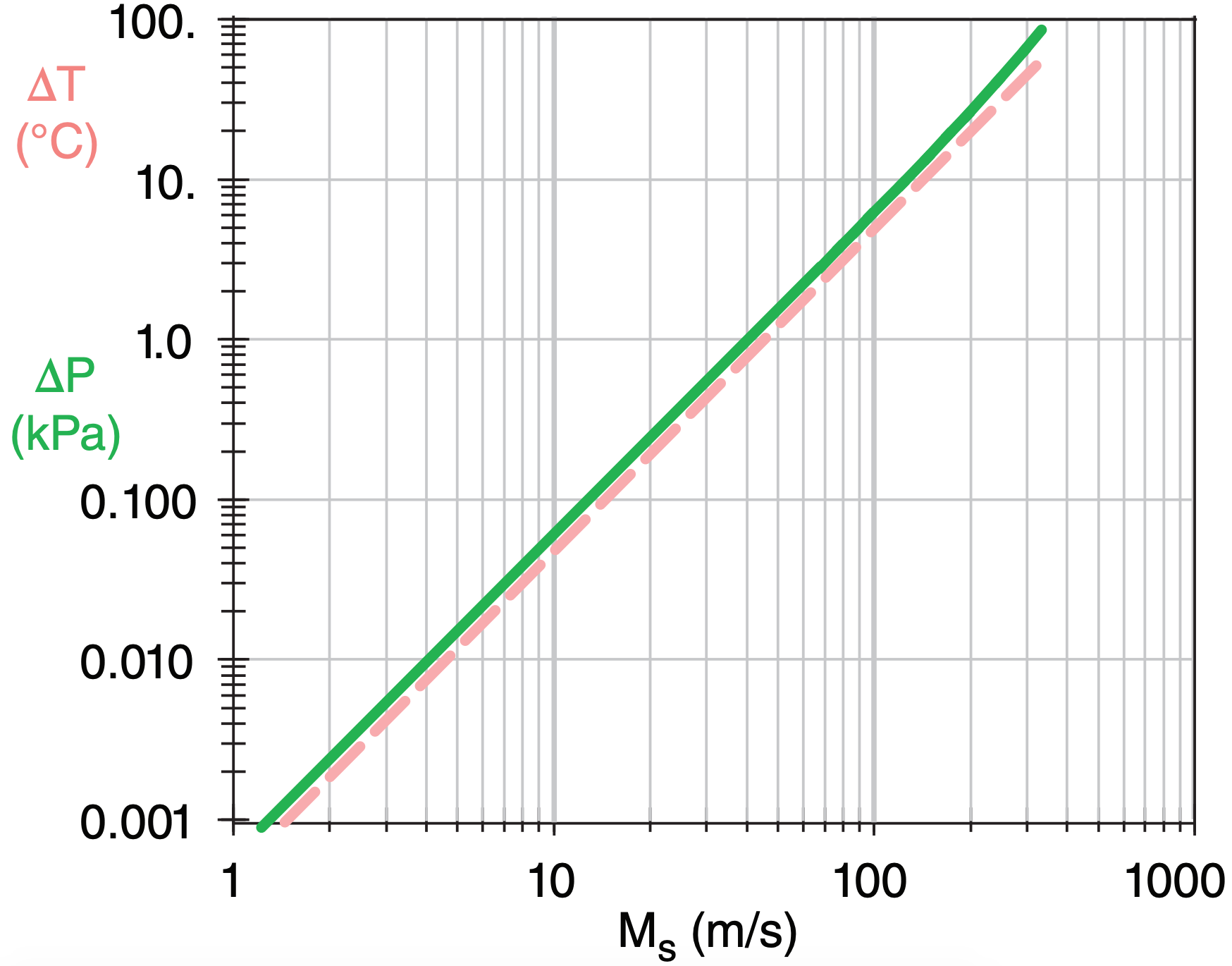
This effect is called dynamic warming or dynamic heating — an effect that you must consider when deploying thermometers in the wind, because the wind will stagnate when it hits the thermometer. As shown in Fig. 17.35, dynamic warming (∆T = To – T) is negligible (∆T ≤ 0.2°C) for flow speeds of Ms ≤ 20 m s–1.
However, for thermometers on an aircraft moving 100 m s–1 relative to the air, or for stationary thermometers exposed to tornadic winds of Ms = 100 m s–1, the dynamic warming is roughly ∆T ≈ 5°C. For these extreme winds you can correct for dynamic warming by using the dynamic temperature To measured by the thermometer, and using the measured wind speed Ms, and then solving eq. (17.47) for free-stream temperature T.
In the Heat Budgets chapter is a relationship between temperature and pressure for an adiabatic, compressible process. Using this with the equation above allows us to solve for the stagnation pressure:
\(\ \begin{align} P_{o}=P_{s} \cdot\left(\frac{T_{o}}{T}\right)^{c_{p} / \Re}\tag{17.48}\end{align}\)
or
\(\ \begin{align} P_{o}=P_{s} \cdot\left(1+\frac{0.5 \cdot M_{s}^{2}}{C_{p} \cdot T}\right)^{c_{p} / \Re}\tag{17.49}\end{align}\)
where Cp/ℜ ≈ Cpd/ℜd = 3.5 for air, Ps is static (freestream) pressure, Ms is free-stream wind speed along the streamline, Cp ≈ Cpd = 1004 J·kg–1·K–1, T is free-stream temperature, and subscript d denotes dry air. Fig. 17.35 shows stagnation-pressure increase with increasing flow speed.
For wind speeds of Ms < 100 m s–1, the previous equation is very well approximated by the simple Bernoulli equation for incompressible flow:
\(\ \begin{align} P_{o}=P_{s}+\frac{\rho}{2} M_{s}^{2}\tag{17.50}\end{align}\)
where ρ is air density. Do not use eq. (17.50) to find dynamic heating when combined with the ideal gas law, because it neglects the large density changes that occur in high-speed flows that stagnate.
Sample Application
Tornadic winds of 100 m s–1 and 30°C blow into a garage and stagnate. Find stagnation T & P. What net force pushes against a 3 x 5 m garage wall?
Find the Answer
Given: Ms =100 m s–1, T=30°C, Wall area A=3x5 =15 m2
Find: Fnet = ? N. Assume: ρ = 1.2 kg m–3, P = 100 kPa.
Use eq. (17.47): To = (30°C)+[(100m s–1)2/(2 · 1004m2·s–2·K–1) = 35°C.
Use eq. (17.48): Po = (100 kPa)·[(35+273)/(30+273)]3.5 = 105.9 kPa.
Compare with eq. (17.50): Po = (100kPa) + [(0.5 · 1.2kg m–3)·(100m s–1)2]·(1 kPa/1000Pa)= 106 kPa
Fnet = ∆P·A = (6 kN m–2)·(15 m2) = 90 kN
Check: Units OK. Physics OK.
Exposition: This force is equivalent to the weight of more than 1000 people, and acts on all walls and the roof. It is strong enough to pop the whole roof up off of the house. Then the walls blow out, and the roof falls back down onto the floor.
Hide in the basement. Quickly.
The previous three equations show that the pressure increase due to stagnation (∆P = Po – Ps) is small (∆P < 0.25 kPa) compared to ambient atmospheric pressure (Ps = 100 kPa) for wind speeds of Ms < 20 m s–1.
Dynamic effects make it difficult to measure static pressure in the wind. When the wind hits the pressure sensor, it decelerates and causes the pressure to increase. For this reason, static pressure instruments are designed to minimize flow deceleration and dynamic errors by having pressure ports (holes) along the sides of the sensor where there is no flow toward or away from the sensor.
Dynamic pressure can be used to measure wind speed. An instrument that does this is the pitot tube. Aircraft instruments measure stagnation pressure with the pitot tube facing forward into the flow, and static pressure with another port facing sideways to the flow to minimize dynamic effects. The instrument then computes an “indicated airspeed” from eq. (17.49 or 17.50) using the pitot – static pressure difference.
During tornadoes and hurricanes, if strong winds encounter an open garage door or house window, the wind trying to flow into the building causes pressure inside the building to increase dynamically. As is discussed in a Sample Application, the resulting pressure difference across the roof and walls of the building can cause them to blow out so rapidly that the building appears to explode.
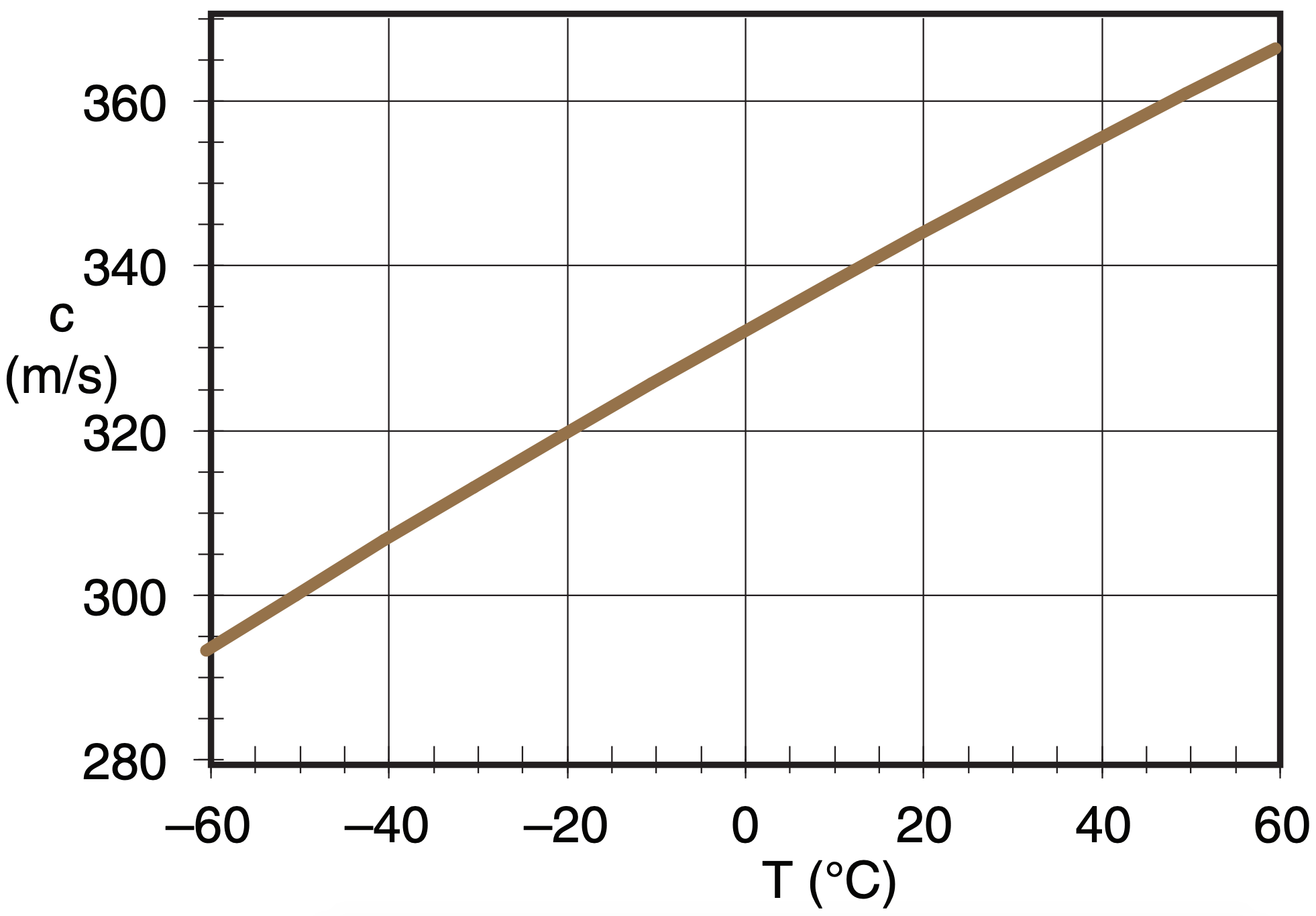
The speed c of sound in air is
\(\ \begin{align} c=[k \cdot \mathfrak{R} \cdot T]^{1 / 2}\tag{17.42}\end{align}\)
where k = Cp/Cv is the ratio of specific heats for air, ℜ is the ideal gas law constant, and T is absolute temperature. [See the INFO box in Chapter 3, section 3.2.3, for a review of specific heats at constant pressure Cp and constant volume Cv.] For dry air, the constants are: k = Cpd/Cvd = 1.4, and ℜd = 287.053 (m2 s–2)·K–1. Thus, the speed of sound increases with the square root of absolute temperature.
The speed M of any object such as an aircraft or an air parcel can be compared to the speed of sound:
\(\ \begin{align} M a=M / c\tag{17.43}\end{align}\)
where Ma is the dimensionless Mach number. Thus, an object moving at Mach 1 is traveling at the speed of sound.
17.9.2.2. Venturi Effect
Bernoulli’s equation says that if velocity increases in the region of flow constriction, then pressure decreases. This is called the Venturi effect.
For gap winds of constant depth, eq. (17.37) can be written as
\(\ \begin{align} \frac{1}{2} M_{s}^{2}+\frac{P_{s}}{\rho}=\frac{1}{2} M_{d}^{2}+\frac{P_{d}}{\rho}\tag{17.51}\end{align}\)
which can be combined with eq. (17.23) to give the Venturi pressure decrease:
\(\ \begin{align} P_{d}-P_{s}=\frac{\rho}{2} \cdot M_{s}^{2} \cdot\left[1-\left(\frac{D_{s}}{D_{d}}\right)^{2}\right]\tag{17.52}\end{align}\)
Unfortunately, gap flows are often not constant depth, because the temperature inversion that caps these flows are not rigid lids.
Sample Application
If a 20 km wide band of winds of 5 m s–1 must contract to pass through a 2 km wide gap, what is the pressure drop in the gap compared to the non-gap flow?
Find the Answer
Given: Ds = 20 km, Dd = 2 km, Ms = 5 m s–1.
Find: Md = ? m s–1.
Assume: ρ = 1.2 kg m–3.
Use eq. (17.52): ∆P = (1.2 kg·m–3/2)·(5m s–1)2·[1 – ((20 km)/(2 km))2]
= –1485 kg·m–1·s–2 = –1.5 kPa
Check: Units OK. Physics OK.
Exposition: This is a measurable drop in atmospheric pressure. The pressure measured at weather stations in such gaps should be compensated for this venturi effect to calculate the effective static pressure, such as could be used in analyzing weather maps.


