17.6: Coastally Trapped Low-level (Barrier) Jets

Last updated
Save as PDF

Page ID: 9643

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Coriolis force is also important in locations such as the eastern Pacific Ocean, where coastally trapped low-level wind jets form parallel to the west coast of N. America. Similar barrier jets can form at other mountain ranges. These jets have dynamics that are very similar to the dynamics of long-gap winds.

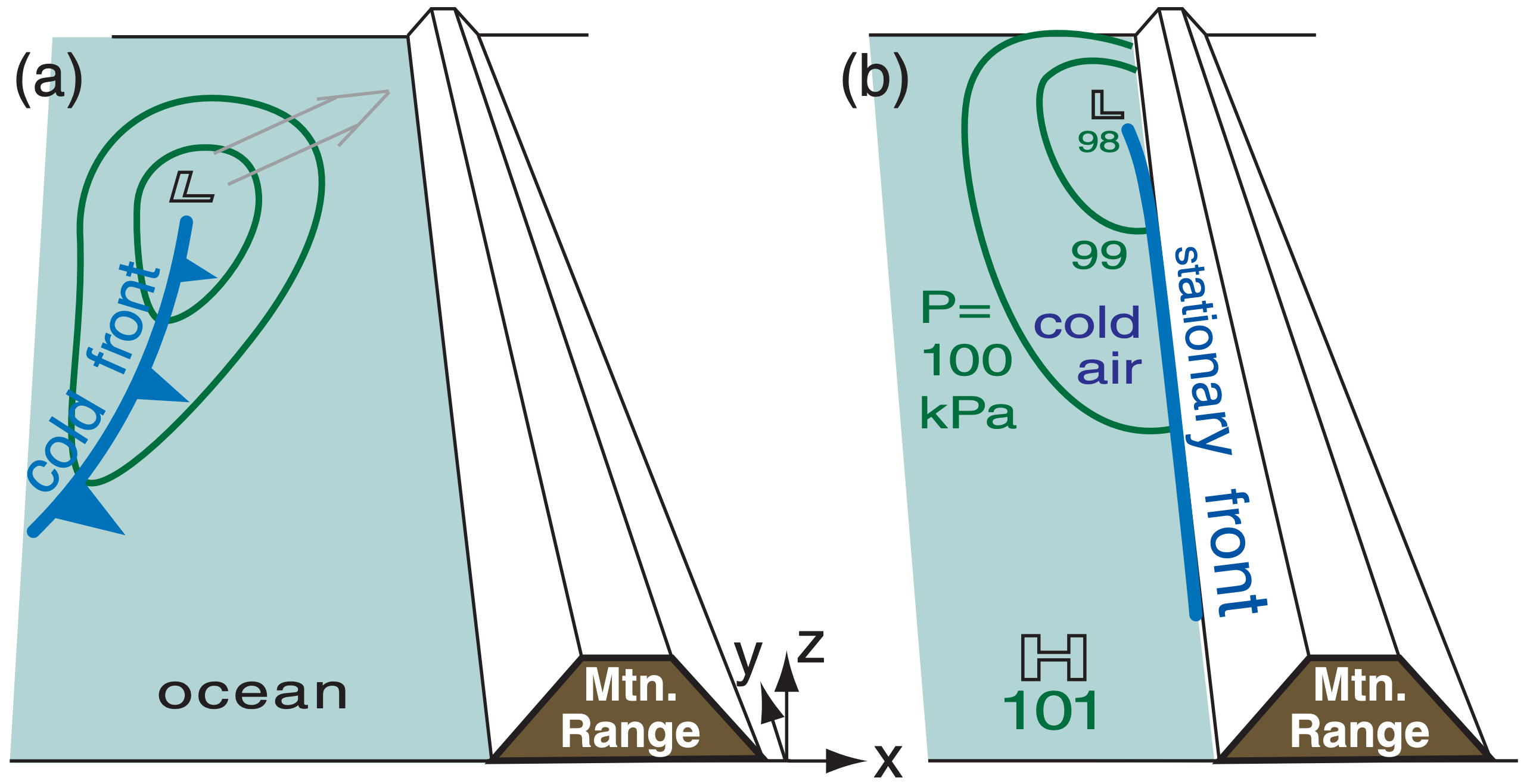
Screen Shot 2020-03-30 at 9.59.57 PM.png — Figure 17.26 (a) Precursor synoptic conditions, as a low L center approaches a coastal mountain (Mtn.) range in the N. Hemisphere. Curved green lines are isobars at sea level. (b) Conditions later when the low reaches the coast, favoring coastally trapped low-level jets.

Consider situations where synoptic-scale lowpressure systems reach the coast of N. America and encounter mountain ranges. Behind the approaching cyclone is cold air, the leading edge of which is the cold front (Fig. 17.26a). The cold air stops advancing eastward when it hits the mountains, causing a stationary front along the ocean side of the mountain range (Fig. 17.26b).

A pressure gradient forms parallel to the mountain range (Fig. 17.26b), between the low (L) center to the north and higher pressure (H) to the south. Fig. 17.27 shows a zoomed view of the resulting situation close to the mountains. The isobars are approximately perpendicular to the mountain-range axis, not parallel as was the case for gap winds.

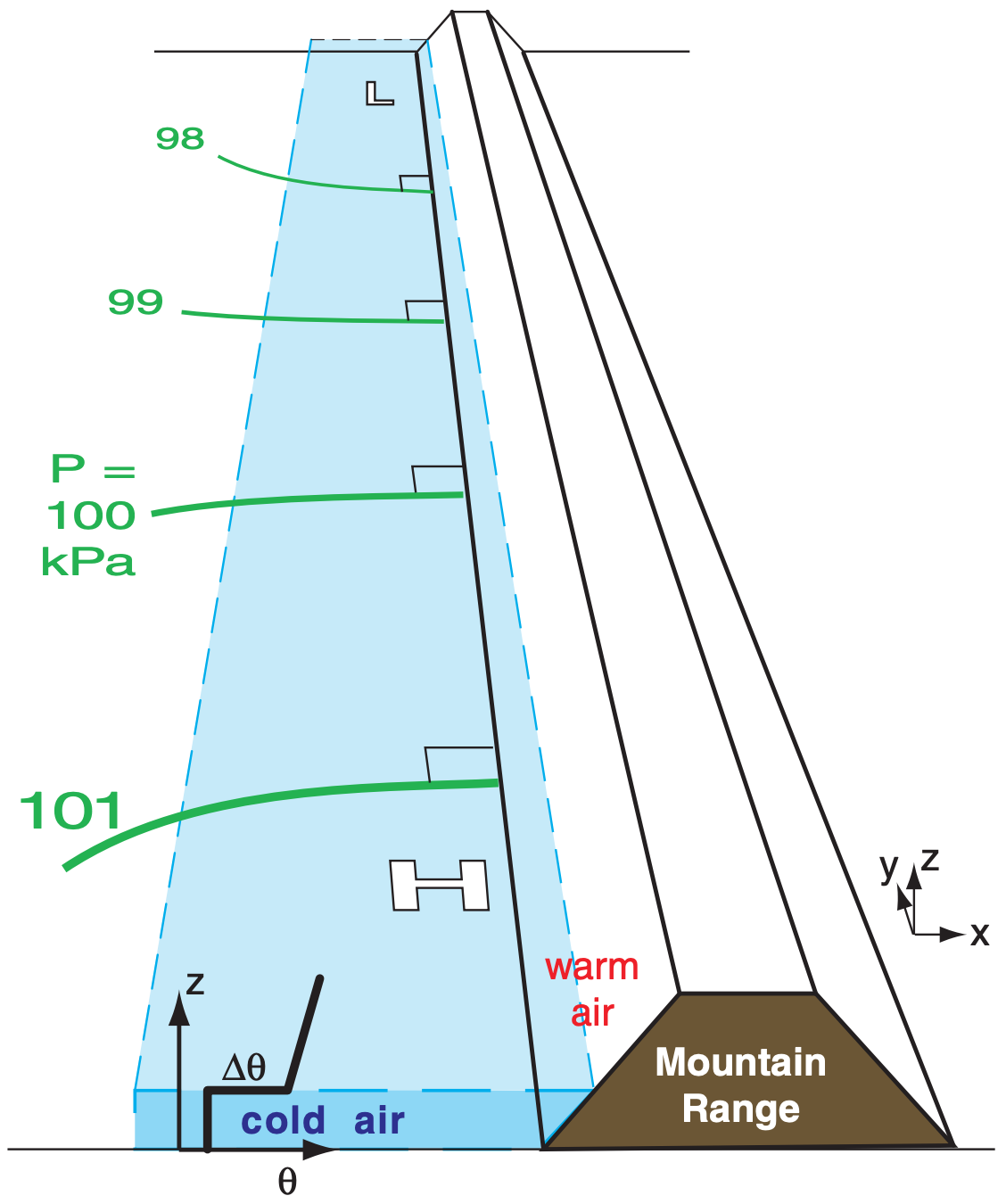
Screen Shot 2020-03-30 at 10.01.51 PM.png — Figure 17.27 Synoptic conditions that favor creation of a mesoscale low-level jet parallel to the coast. Curved green lines are isobars, H and L are high and low-pressure centers, and θ is potential temperature.

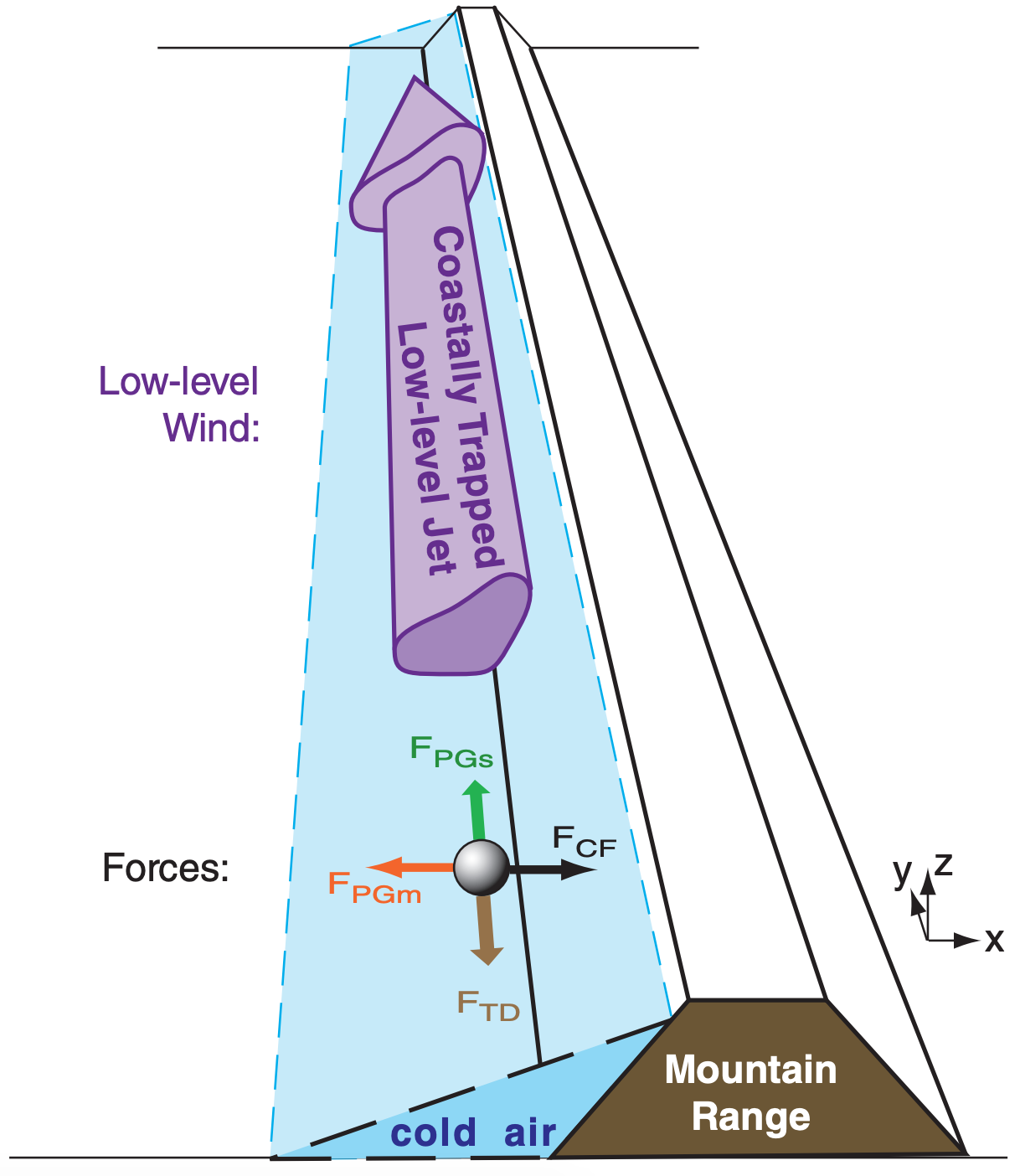
Screen Shot 2020-03-30 at 10.05.05 PM.png — Figure 17.28 Final force (F) balance and cold-air location during a coastally trapped low-level jet (fast winds parallel to the coast). Vertical scale is stretched roughly 100:1 relative to the horizontal scale

As the synoptic-scale pressure gradient (PGs) accelerates the cold air from high towards low, Coriolis force (CF) turns this air toward the right (in the N. Hem.) causing the cold air to ride up along the mountain range. This creates a mesoscale pressure gradient (PGm) pointing down the cold-air slope (Fig. 17.28). Eventually an equilibrium is reached where turbulent drag (TD) nearly balances the synoptic pressure-gradient force, and Coriolis force is balanced by the mesoscale pressure gradient.

The end result is a low-altitude cold wind parallel to the coast, just west of the mountain range. The jet-core height is located vertically about 1/3 of the distance from the ocean (or lowland floor) to the ridge top. Jet core altitudes of 50 to 300 m above sea level have been observed along the west coast of N. America, while altitudes of about 1 km have been observed for barrier jet cores in California west of the Sierra-Nevada mountain range. Maximum speeds of 10 to 25 m s^–1 have been observed in the jet core.

Width of the coastal jet is on the order of 100 to 150 km. This width is roughly equal to the Rossby radius of deformation, λ_R, which is a measure of the upstream region of influence of the mountain range on a flow that is in geostrophic balance. For a cold marine layer of air capped by a strong inversion as sketched in Fig. 17.28, the external Rossby radius of deformation is

\(\ \begin{align} \lambda_{R}=\frac{\sqrt{|g| \cdot h \cdot \Delta \theta_{v} / T_{v}}}{f_{c}}\tag{17.28}\end{align}\)

where|g| = 9.8 m·s^–2 is gravitational acceleration magnitude, h is mountain range height, f_c is the Coriolis parameter, ∆θ_v is the jump of virtual potential temperature at the top of the marine air layer, and T_v is an average absolute virtual temperature of the air. For a statically-stable layer of air having a linear increase of potential temperature with height instead of a step discontinuity, an internal Rossby radius of deformation is

\(\ \begin{align} \lambda_{R}=\frac{N_{B V} \cdot h}{f_{c}}\tag{17.29}\end{align}\)

where N_BV = [(|g|/T_v) · ∆θ_v/∆z] ^1/2 is the Brunt-Väisälä frequency.

Sample Application

The influence of the coast mountains extends how far to the west of the coastline in Fig. 17.28? The cold air has virtual potential temperature 8°C colder than the neighboring warm air. The latitude is such that the Coriolis parameter is 10^–4 s^–1. Mountain height is 2000 m.

Find the Answer

Given: h = 2000 m, ∆θv = 8°C = 8 K, f_c = 10^–4 s^–1.

Find: λ_R = ? km, external Rossby deformation radius

Assume: |g|/T_v = 0.03333 m·s^–2·K^–1

The region of influence extends a distance equal to the Rossby deformation radius. Thus, use eq. (17.28):

λ_R = [(0.03333 m·s^–2·K^–1)·(2000 m)·(8 K)]^1/2 /(10^–4 s^–1) = 231,000 m = 231 km

Check: Units OK. Magnitude OK.

Exposition: Even before fronts and low-pressure centers hit the coastal mountains, the mountains are already influencing these weather systems hundreds of kilometers offshore.