17.4: Open-channel Hydraulics
- Page ID
- 9641
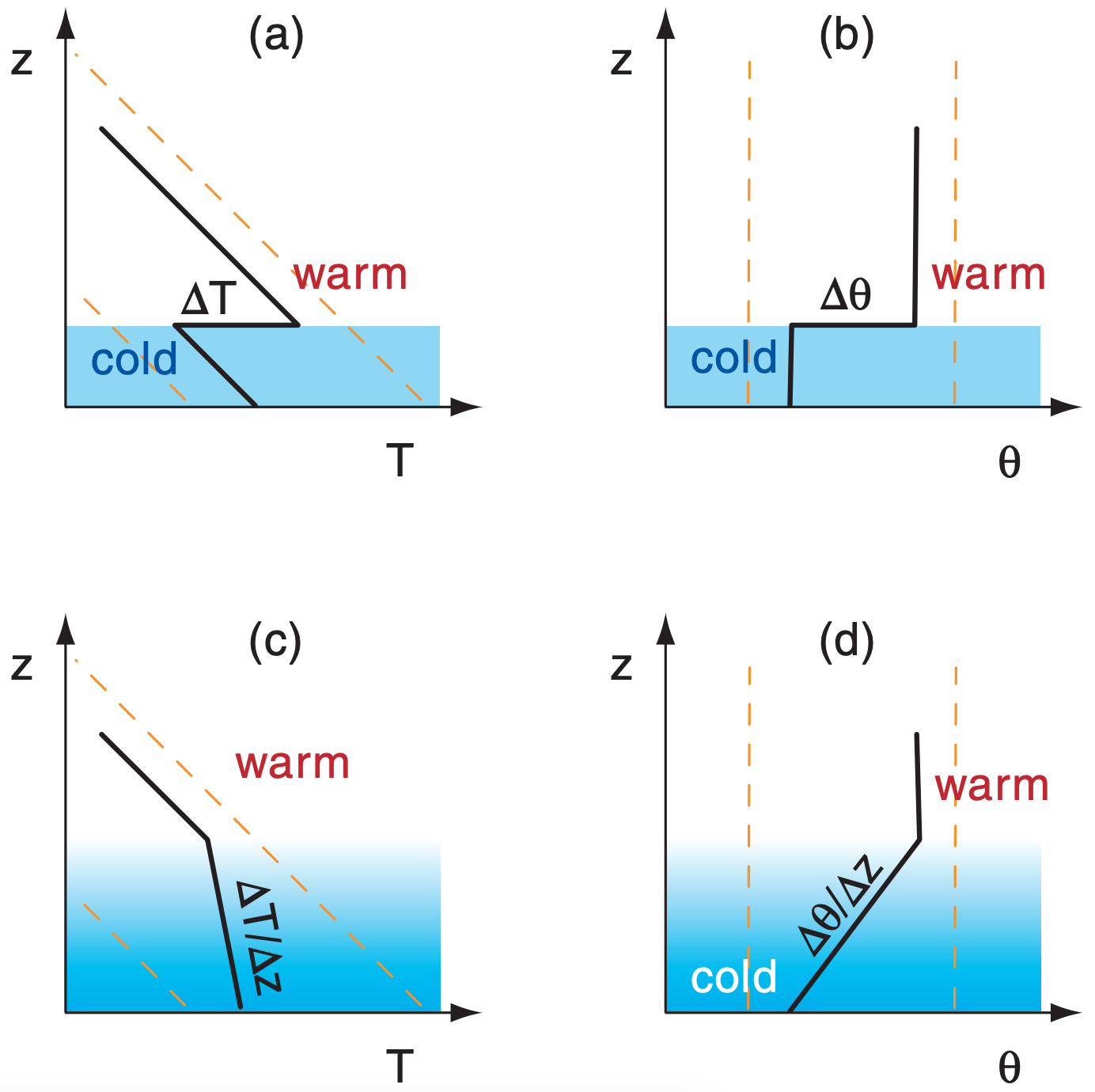
Sometimes a dense cold-air layer lies under a lessdense warmer layer, with a relatively sharp temperature discontinuity (∆T = ∆θ) between the two layers (Fig. 17.15a and b). This temperature jump marks the density interface between the two layers. Examples of such a two-layer system include arctic air advancing behind a cold front and sliding under warmer air, cold gust fronts from thunderstorms, and cool marine air moving inland under warmer continental air.
These two-layer systems behave similarly to water in an open channel — a two layer system of dense water under less-dense air. Hence, you can apply hydraulics (applications of liquid flow based on its mechanical properties) to the atmosphere, for cases where air compressibility is not significant.
Sometimes the cold air can be stably stratified (Figs. 17.15c & d) as idealized here with constant lapse rate, where ∆θ/∆z = ∆T/∆z + Γd , using the dry adiabatic lapse rate Γd = 9.8 °C km–1. You can use modified hydraulic theory for these cases.
Hydraulic theory depends on the speed of waves on the interface between cold and warm air.
Because hydraulics depends on density, it is more accurate to use virtual temperature instead of temperature, to include the effect of humidity on air density. Namely, use Tv instead of T, use ∆Tv instead of ∆T, and ∆θv instead of ∆θ.
These two-layer systems behave similarly to water in an open channel — a two layer system of dense water under less-dense air. Hence, you can apply hydraulics (applications of liquid flow based on its mechanical properties) to the atmosphere, for cases where air compressibility is not significant.
Sometimes the cold air can be stably stratified (Figs. 17.15c & d) as idealized here with constant lapse rate, where ∆θ/∆z = ∆T/∆z + Γd , using the dry adiabatic lapse rate Γd = 9.8 °C km–1. You can use modified hydraulic theory for these cases.
Hydraulic theory depends on the speed of waves on the interface between cold and warm air.
17.4.1. Wave Speed

Waves (vertical oscillations that propagate horizontally on the density interface) can exist in air (Fig. 17.16), and behave similarly to water waves. For hydraulics, if water in a channel is shallow, then long-wavelength waves on the water surface travel at the intrinsic “shallow-water” phase speed co of:
\(\ \begin{align} c_{o}=\sqrt{|g| \cdot h}\tag{17.14}\end{align}\)
where |g| = 9.8 m s–2 is gravitational acceleration magnitude, and h is average water depth. Intrinsic phase speed is the speed of propagation of any wave crest relative to the mean fluid motion.
For a two-layer air system, the effect of gravity is reduced because it depends on the relative buoyancy between the warm and cold air layers. Define a reduced gravity as |g’|= |g|·∆θv/Tv. For a shallow bottom layer, the resulting intrinsic phase speed of surface waves on the interface between the coldand warm-air layers is:
\(\ \begin{align} c_{o}=\sqrt{\left|g^{\prime}\right| \cdot h}=\left(|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot h\right)^{1 / 2}\tag{17.15}\end{align}\)
where ∆θv is the virtual potential temperature jump between the two air layers, Tv is an average absolute virtual temperature (in Kelvin), h is the depth of the cold layer of air, and |g| = 9.8 m·s–2 is gravitational acceleration magnitude.
The speed that wave energy travels through a fluid is the group speed cg. Group speed is the speed that hydraulic information can travel relative to the mean flow velocity, and it determines how the upstream flow reacts to downstream flow changes. For a two-layer system with bottom-layer depth less than 1/20 the wavelength, the group speed equals the phase speed
\(\ \begin{align} c_{g}=c_{o}\tag{17.16}\end{align}\)
Sample Application
For a two-layer air system with 5°C virtual potential temperature difference across the interface and a bottom-layer depth of 20 m, find the intrinsic group speed, and compare it to the speed of a water wave.
Find the Answer
Given: ∆θv = 5°C = 5K, h = 20 m. Assume Tv = 283 K
Find: cg = ? m s–1, for air and for water
For a 2-layer air system, use eqs. (17.15 & 17.16):
cg = co = [(9.8 m·s–2)·(5K)·(20m)/(283K)]1/2 = 1.86 m s–1
For water under air, use eq. (17.14 & 17.16)):
cg = co = [(9.8 m·s–2)·(20m)]1/2 = 14 m s–1
Check: Units OK. Magnitude OK.
Exposition: Atmospheric waves travel much slower than channel or ocean waves, and have much longer wavelengths. This is because of the reduced gravity |g’| for air, compared to the full gravity |g| for water.
For a statically-stable atmospheric system with constant lapse rate, there is no surface (no interface) on which the waves can ride. Instead, internal waves can exist that propagate both horizontally and vertically inside the statically stable region. Internal waves reflect from solid surfaces such as the ground, and from statically neutral layers.
For internal waves, the horizontal component of group velocity ug depends on both vertical and horizontal wavelength λ. To simplify this complicated situation, focus on infinitely-long waves in the horizontal (which propagate the fastest in the horizontal), and focus on a wave for which the vertical wavelength is proportional to the depth h of the statically stable layer of air. Thus:
\(\ \begin{align}u_{g}=N_{B V} \cdot h=\left(\frac{|g|}{T_{v}} \cdot \frac{\Delta \theta_{v}}{\Delta z}\right)^{1 / 2} \cdot h\tag{17.17}\end{align}\)
where NBV is the Brunt-Väisälä frequency, and ∆θv/ ∆z is the vertical gradient of virtual potential temperature (a measure of static-stability strength).
17.4.2. Froude Number - Part 1
The ratio of the fluid speed (M) to the wave group velocity (cg , the speed that energy and information travels) is called the Froude number Fr.
\(\ \begin{align}F r=M / c_{g}\tag{17.18}\end{align}\)
At least three different Froude numbers can be defined, depending on the static stability and the flow situation. We will call these Fr1, Fr2, and Fr3, the last of which will be introduced in a later section.
For surface (interfacial) waves in an idealized atmospheric two-layer system where cg = co = (|g’|·h) 1/2, the Froude number is Fr1 = M/co:
\(\ \begin{align} F r_{1}=\frac{M}{\left(|g| \cdot \frac{\Delta \theta_{v}}{T_{v}} \cdot h\right)^{1 / 2}}\tag{17.19}\end{align}\)
where h is the depth of the bottom (cold) air layer, ∆θv is the virtual potential temperature jump between the two air layers, Tv is an average absolute virtual temperature (in Kelvins), and |g| = 9.8 m·s–2 is gravitational acceleration magnitude.
For the other situation of a statically stable region supporting internal waves, the Froude number is Fr2 = M/ug :
\(\ \begin{align} F r_{2}=\frac{M}{\left(\frac{|g|}{T_{v}} \cdot \frac{\Delta \theta_{v}}{\Delta z}\right)^{1 / 2} \cdot h}\tag{17.20}\end{align}\)
The nature of the flow is classified by the value of the Froude number:
- subcritical (tranquil) for Fr < 1
- critical for Fr = 1
- supercritical (rapid) for Fr > 1
For subcritical flow, waves and information travel upstream faster than the fluid is flowing downstream, thus allowing the upstream flow to “feel” the effect of both upstream conditions and downstream conditions such as flow constrictions. For supercritical flow, the fluid is moving so fast that no information can travel upstream (relative to a fixed location); hence, the upstream fluid does not “feel” the effects of downstream flow constrictions until it arrives at the constriction. For airflow, the words (upwind, downwind) can be used instead of (upstream, downstream).
Sample Application
For a two-layer air system with 5°C virtual potential temperature difference across the interface and a bottom-layer depth of 20 m, find the Froude number if the average flow speed is 5 m s–1. Discuss whether the flow is critical.
Find the Answer
Given: ∆θv = 5°C = 5K, h = 20 m. M = 5 m s–1. Assume Tv = 283 K
Find: Fr1 = ? (dimensionless)
For a 2-layer air system, use eq. (17.19):
Fr1 = (5 m s–1) / [(9.8 m·s–2)·(5K)·(20m)/(283K)]1/2
= (5 m s–1) / (1.86 m s–1) = 2.69
Check: Units OK. Magnitude OK.
Exposition: This flow is supercritical. Hence, the air blows the wave downwind faster than it can propagate upwind against the mean flow.
Sample Application
For a smooth virtual potential-temperature gradient of 5°C across a stable-layer depth of 20 m, find the Froude number if the average flow speed is 5 m s–1. Discuss whether the flow is critical.
Find the Answer
Given: ∆θv = 5°C = 5K, ∆z = h = 20 m. Assume Tv = 283 K
Find: Fr2 = ? (dimensionless)
Use eq. (17.20). But since ∆z = h , this causes eq. (17.20) to reduce to eq. (17.19). Hence, we get the same answer as in the previous Sample Application:
Fr2 = 2.69
Check: Units OK. Magnitude OK.
Exposition: This flow is also supercritical. Although this example was contrived to give the same virtual potential temperature gradient across the whole fluid depth as before, often this is not the case. So always use eq. (17.20) for a constant stable stratification flow, and don’t assume that it always reduces to eq. (17.19).
17.4.3. Conservation of Air Mass
Consider a layer of well-mixed cold air flowing at speed Ms along a wide valley of width Ds. If it encounters a constriction where the valley width shrinks to Dd (Fig. 17.17), the winds will accelerate to Md to conserve the amount of air mass flowing. If the depth h of the flow is constant (not a realistic assumption), then air-mass conservation gives:
\(\ \begin{align}mass\ flowing\ \underline{out} = mass\ flowing\ \underline{in}\tag{17.21}\end{align}\)
ρ · volume flowing out = ρ · volume flowing in
\(\ \begin{align} \rho \cdot M_{d} \cdot h \cdot D_{d}=\rho \cdot M_{s} \cdot h \cdot D_{s}\tag{17.22}\end{align}\)
Thus,
\(\ \begin{align} M_{d}=\frac{D_{s}}{D_{d}} \cdot M_{s}\tag{17.23}\end{align}\)
under the assumptions of negligible changes in air density ρ. Thus, the flow must become faster in the narrower valley.
Sample Application
If a 20 km wide band of winds of 5 m s–1 must contract to pass through a 2 km wide gap, what is the wind speed in the gap.
Find the Answer
Given: Ds = 20 km, Dd = 2 km, Ms = 5 m s–1.
Find: Md = ? m s–1
Use eq. (17.23): Md = [(20km)/(2km)]·(5m s–1) = 50 m s–1
Check: Units OK. Physics OK.
Exposition: The actual winds would be slower, because turbulence would cause significant drag.
Similarly, suppose air is flowing downhill through a valley of constant-width D. Cold air of initial speed Ms might accelerate due to gravity to speed Md further down the slope. Air-mass conservation requires that the depth of the flow hd in the high speed region be less than the initial depth hs in the lower-speed region.
\(\ \begin{align} h_{d}=\frac{M_{s}}{M_{d}} \cdot h_{s}\tag{17.24}\end{align}\)
17.4.4. Hydraulic Jump
Consider a layer of cold air flowing supercritically in a channel or valley. If the valley geometry or slope changes at some downstream location and allows wind speed M to decrease to its critical value (Fr = 1), there often occurs a sudden increase in flow depth h and a dramatic increase in turbulence. This transition is called a hydraulic jump. Downstream of the hydraulic jump, the wind speed is slower and the flow is subcritical.
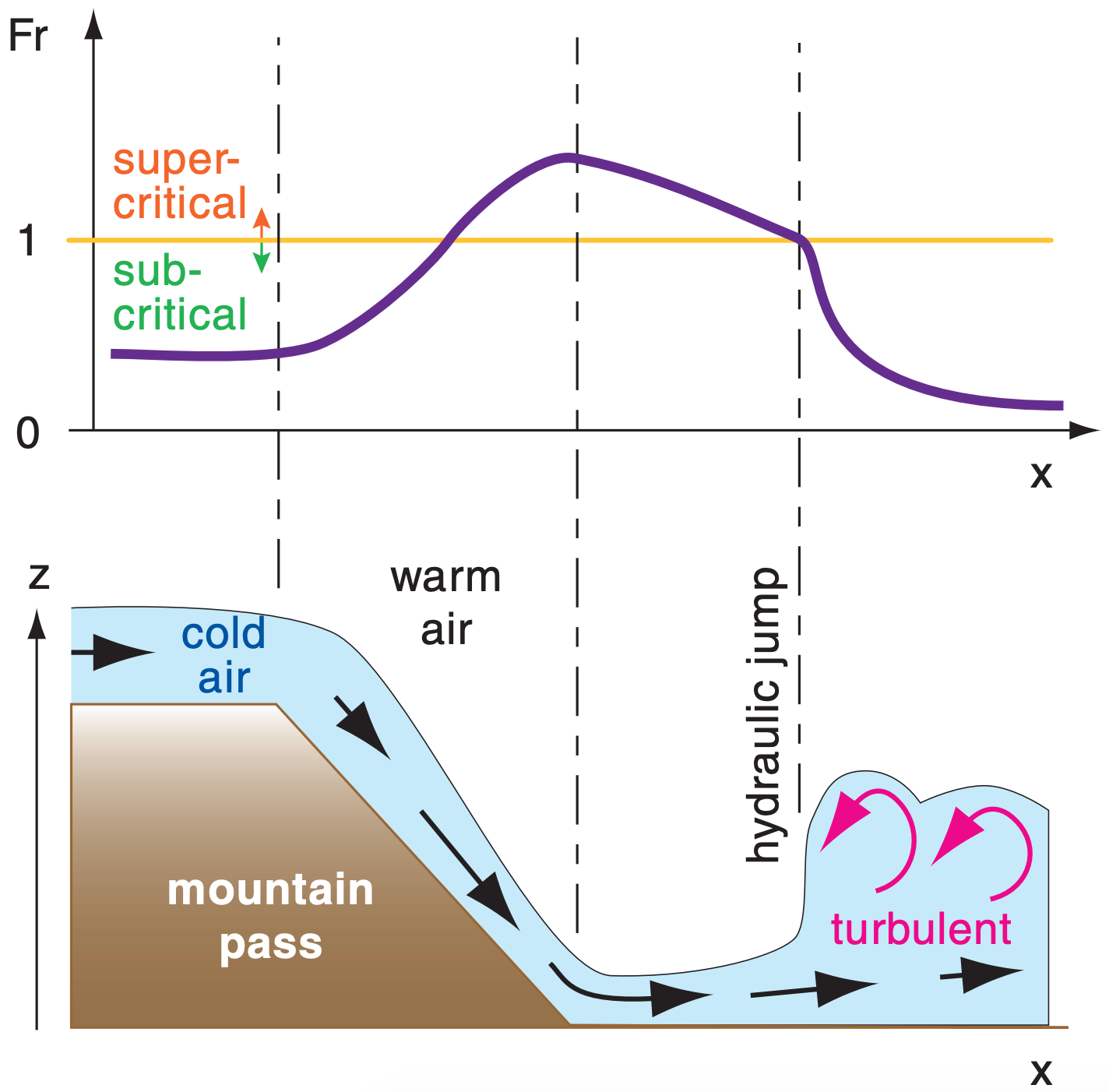
In Fig. 17.18, you can consider the hydraulic jump as a wave that is trying to propagate upstream. However, the cold air flowing downslope is trying to wash this wave downstream. At the hydraulic jump, the wave speed exactly matches the opposing wind speed, causing the wave to remain stationary relative to the ground.
For example (Fig. 17.18), consider cold air flowing down a mountain slope. It starts slowly, and has Fr < 1. As gravity accelerates the air downslope and causes its depth to decrease, the Froude can eventually reach the critical value Fr = 1. As the air continues to accelerate downhill the flow can become supercritical (Fr > 1). But once this supercritical flow reaches the bottom of the slope and begins to decelerate due to turbulent drag across the lowland, its velocity can decrease and the flow depth gradually increases. At some point downstream the Froude number again reaches its critical value Fr = 1. A hydraulic jump can occur at this point, and turbulent drag increases. If this descending cold air is foggy or polluted, the hydraulic jump can be visible.


