8.1: Weather Satellites
- Page ID
- 9576
8.2.1. Orbits
Artificial satellites such as weather satellites orbiting the Earth obey the same orbital mechanics as planets orbiting around the sun. For satellites in near-circular orbits, the pull by the Earth’s gravity \(f_G\) balances centrifugal force \(f_C\) :
\[\ \begin{align} f_{G} &=\frac{G \cdot M \cdot m}{R^{2}}\tag{8.6} \\ f_{C} &=\left(\frac{2 \pi}{t_{o r b i t}}\right)^{2} \cdot m \cdot R\tag{8.7}\end{align}\]
where \(R\) is the distance between the center of the Earth and the satellite, m is the mass of the satellite, \(M\) is the mass of the Earth (5.9742x1024 kg), and \(G\) is the gravitational constant (6.6742x10–11 N·m2·kg–2 ). See Appendix B for lists of constants.
Solve for the orbital time period torbit by setting fG = fC:
\(\ \begin{align} t_{\text {orbit}}=\frac{2 \pi \cdot R^{3 / 2}}{\sqrt{G \cdot M}}\tag{8.8}\end{align}\)
Orbital period does not depend on satellite mass, but increases as satellite altitude increases.
Weather satellite orbits are classified as either polar-orbiting or geostationary (Fig. 8.10). Polarorbiters are low-Earth-orbit (LEO) satellites.

Sample Application
At what (a) distance above the Earth’s center, & (b) altitude above the Earth’s surface, must a geostationary satellite be parked to have an orbital period of exactly one sidereal day? Use Appendix B for Earth constants.
Find the Answer
Given: torbit = 23.934 469 6 h = 86,164 s = sidereal day.
M = 5.973 6 x 1024 kg
G = 6.674 28 x 10–11 m3·s–2·kg–1
Find: (a) R = ? km, (b) z = ? km
(a) Rearrange eq. (8.8):
R = ( torbit / 2π ) 2/3 · (G · M) 1/3 = 42,167.5 km
(b) From this subtract Earth radius at equator
( Ro = 6,378 km ) to get height above the surface:
z = R – Ro = 35,790 km
Check: Units OK. Physics OK.
Exposition: This compares well with real satellites. The GOES-15 target orbit is z = 35,780 km. If satellites are too high, they orbit too slowly, causing them to gradually get behind of the Earth’s rotation. Namely, they would drift a small amount each day toward the west relative to a fixed point on the Earth’s surface.
Such drift is normal for satellites, which is why they carry propellant to make orbital adjustments, as commanded by tracking stations on the ground.
For a calendar day (24 h from sun overhead to sun overhead), the Earth must rotate 360.9863°, because the position of the sun relative to the fixed stars changes as the Earth moves around it.
8.2.1.1. Geostationary Satellites
Geostationary satellites are in high Earth orbit over the equator, so that the orbital period matches the Earth’s rotation. Relative to the fixed stars, the Earth rotates 360° in 23.934 469 6 h, which is the duration of a sidereal day. With this orbital period, geostationary satellites appear parked over a fixed point on the equator. From this vantage point, the satellite can take a series of photographs of the same location, allowing the photos to be combined into a repeating movie called a satellite loop.
Disadvantages of geostationary satellites include the following: distance from Earth is so great that larger magnification is needed to resolve smaller clouds; many satellites must be parked at different longitudes for imagery to cover the globe; imaging might be interrupted during nights near the equinoxes because the solar panels are eclipsed by the Earth and are in darkness; and polar regions are difficult to see.
Satellites have planned lifetimes of about 5 to 17 years, so older satellites must be continually replaced with newer ones. Lifetimes are limited partly because of the limited storage of propellants needed to make orbital corrections. Satellites are also damaged when they are hit at high speed by tiny meteoroids, and by major solar storms. For this reason, most meteorological satellite agencies try to keep an in-orbit spare satellite nearby.
Table 8-1 lists geostationary weather satellites. The USA has Geostationary Operational Environ. Satellites (GOES). The European Org. for the Exploitation of Meteorol. Sat. (EUMETSAT) has Meteosat (MET) (Fig. 8.11). The Japan Meteorol. Agency (JMA) has Himawari. The Chinese Meteorol. Admin. (CMA) has FengYun (“Wind & cloud”). Russia’s Geostat. Operational Meteorol. Sat. (GOMS) program has Elektro-L. The India Space Research Org. (ISRO) has INSAT.
| Table 8-1. Some of the geostationary weather satellites as of March 2017 | ||
| Satellite | Longitude | |
|---|---|---|
| USA | GOES-13 (US East) | 75°W |
| USA | GOES-14 (in-orbit spare | |
| USA | GOES-15 (US West) | 135°W |
| USA | GOES-16 (initial checkout) | |
| EU | Meteosat MET-8 (Indian Ocean) | 41.5°E |
| EU | Meteosat MET-9 (EU rapid scan) | 9.5°E |
| EU | Meteosat MET-10 (Europe | 0° |
| EU | Meteosat MET-11 (in-orbit spare) | |
| Japan | Himawari-8 (Japan & W. Pacific) | 140.7°E |
| Japan | Himawari-9 (in-orbit spare) | |
| China | FengYun FY-4 | 86.5°E |
| China | FengYun FY-4 | 105°E |
| China | FengYun FY-2 | 123.5E |
| Russia | Elektro-L | 76°E |
| India | INSAT-3DR | 74°E |

8.2.1.2. Polar Orbiting Satellites
If geostationary positioning is not required, then weather satellites can be placed at any altitude with any orbital inclination. However, there is a special altitude and inclination that allows satellites to view the Earth at roughly the same local time every day. Advantages are consistent illumination by the sun, lower altitude to better resolve smaller clouds, and good views of high latitudes.
To understand this orbit, consider the following. When the orbital plane of the satellite is along the Earth’s equator, AND the direction of satellite orbit is the same as the direction of Earth’s rotation, then the orbit is defined to have 0° inclination (Fig. 8.12a). Greater inclination angles (Fig. 8.12b) indicate greater tilt of the orbit relative to the equator. For inclinations greater than 90°, the satellite is orbiting opposite to the Earth’s rotation (Fig. 8.12c). For an inclined orbit, the ascending node is the side of the orbit where the satellite crosses the equator northbound (behind the Earth in Fig. 8.12b & c). The descending node is where it crosses the equator southbound (in front of the Earth in Fig. 8.12b & c).

Polar orbiting weather satellites are designed so that the locations of the ascending and descending nodes are sun-synchronous. Namely, the satellite always observes the same local solar times on every orbit. For example, Fig. 8.13a shows a satellite orbit with descending node at about 10:20 AM local time. Namely, the local time at city A directly under the satellite when it crosses the equator is 10:20 AM.
For this sun-synchronous example, 100 minutes later, the satellite has made a full orbit and is again over the equator. However, the Earth has rotated 25.3° during this time, so it is now local noon at city A. However, city B is now under the satellite (Fig. 8.13b), where its local time is 10:20 AM. 100 minutes later, during the next orbit, city C is under the satellite, again at 10:20 AM local time (Fig. 8.13c).
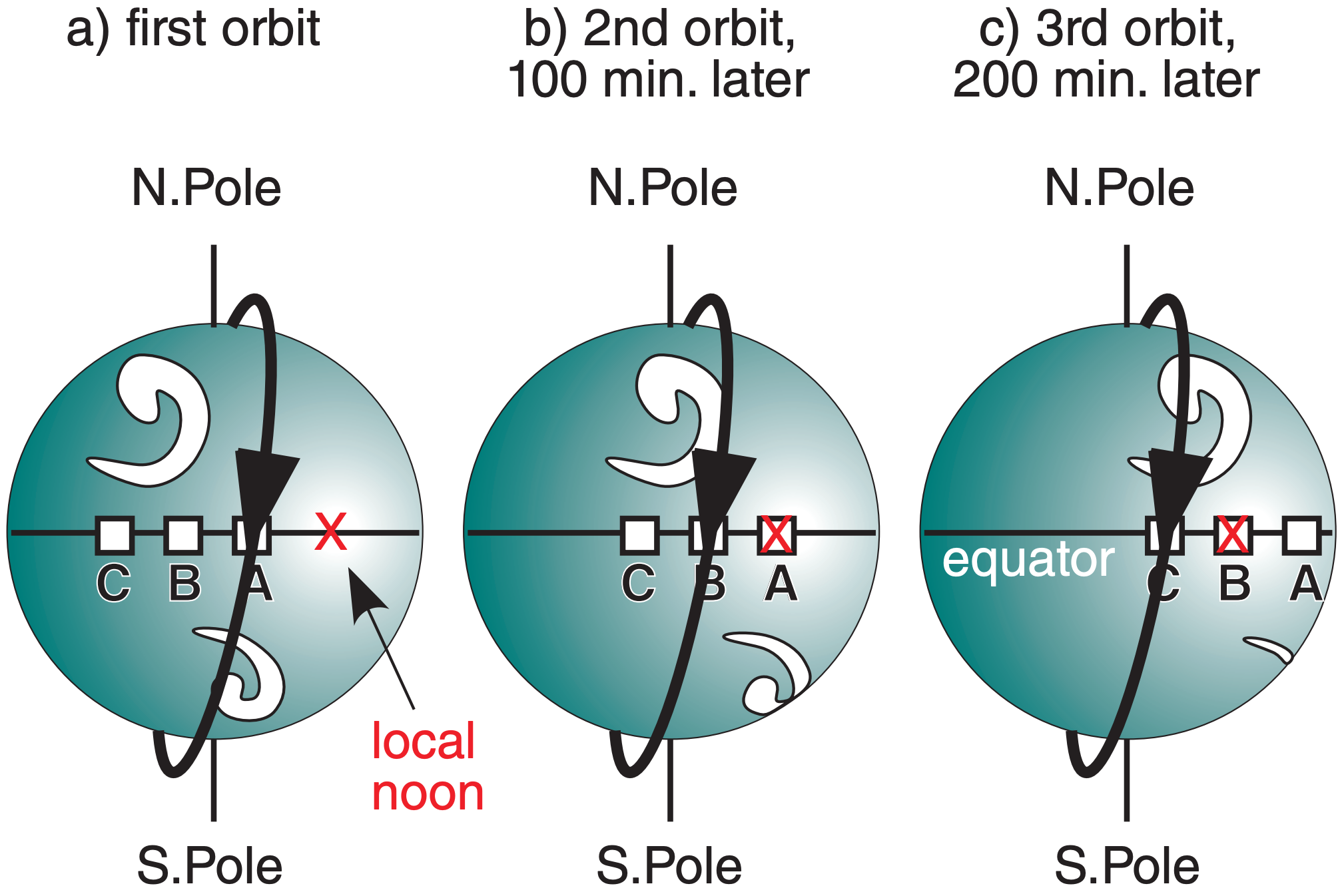
For the satellite orbits in Fig. 8.13, on the back side of the Earth, the satellite always crosses the equator at 10:20 PM local time during its ascension node.
Sun-synchronous polar-orbiting satellites are nicknamed by the time of day when they cross the equator during daylight. It does not matter whether this daylight crossing is during the ascent or descent part of the orbit. For the example of Fig. 8.13, this is the morning or AM satellite.
The USA has Polar Orbiting Environ. Satellite (POES) NOAA-19, launched in Feb 2009. The Suomi National Polar-orbiting Partnership (NPP) satellite (launched Oct 2011) is a transition to future Joint Polar Sat. System (JPSS) satellites. EUMETSAT has 2 Metop satellites in orbit.
For the polar orbit to remain sun-synchronous during the whole year, the satellite orbit must precess 360°/year as the Earth orbits the sun; namely, 0.9863° every day. This is illustrated in Fig. 8.14. Aerospace engineers, astronomers and physicists devised an ingenious way to do this without using their limited supply of on-board propellant. They take advantage of the pull of the solar gravity and the resulting slight tidal bulge of the “solid” Earth toward the sun. As the Earth rotates, this bulge (which has a time lag before disappearing) moves eastward and exerts a small gravitational pull on the satellite in the direction of the Earth’s rotation.
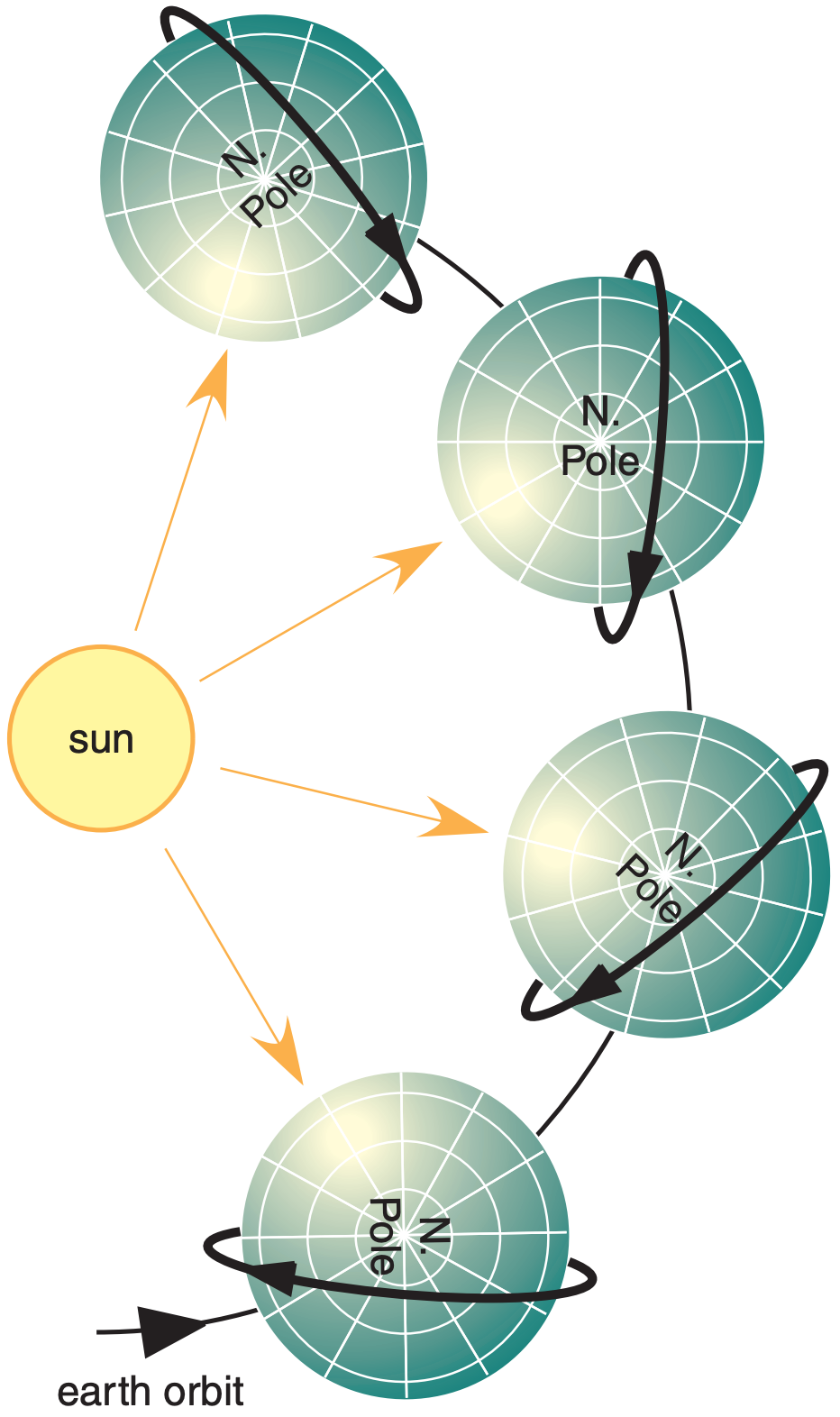
This applies a torque to the orbit to cause it to gradually rotate relative to the fixed stars, so the orbit remains synchronous relative to the sun. The combination of low Earth orbit altitude AND inclination greater than 90° gives just the right amount of precession to maintain the sun-synchronous orbit.
The result is that polar-orbiting weather satellites are usually placed in low Earth orbit at 700 to 850 km altitude, with short orbital periods of 98 to 102 minutes, and inclinations of 98.5° to 99.0°. Polar orbiting satellites do not go directly over the poles, but intentionally miss them by 9°. This is still close enough to get good images of the poles.
8.2.2. Imager
Modern weather satellites have many capabilities, one of which is to digitally photograph (make images of) the clouds, atmosphere, and Earth’s surface. Meteorologists use these photos to help identify and locate weather patterns such as fronts, thunderstorms and hurricanes. Pattern-recognition programs can also use sequences of photos to track cloud motions, thereby inferring the winds at cloudtop level. The satellite instrument system that acquires the digital data to construct these photos is called an imager.
|
Table 8-2. Advanced Baseline Imager (ABI) channels/ bands on USA GOES-16 weather satellite. WV = water vapor. IR = infrared. • Popular old GOES-15 channels for visible, WV & IR. |
|||
| Channel # | Nickname of the Spectral Band | Center Wavelength (µm) | Wavelength Range (µm) |
|---|---|---|---|
| 1 | visible blue | 0.47 | 0.45 - 0.49 |
| 2• | visible red | 0.64 | 0.59 - 0.69 |
| 3 | “veggie” | 0.865 | 0.846 - 0.885 |
| 4 | cirrus | 1.378 | 1.371 - 1.386 |
| 5 | snow/ice | 1.61 | 1.58 - 1.64 |
| 6 | cloud-particle size | 2.25 | 2.225 - 2.275 |
| 7 | shortwave IR window | 3.90 | 3.80 - 4.00 |
| 8• | high troposphere WV | 6.19 | 5.77 - 6.6 |
| 9 | mid-troposphere WV | 6.95 | 6.75 - 7.15 |
| 10 | low-troposphere WV | 7.34 | 7.24 - 7.44 |
| 11 | cloud-top phase | 8.5 | 8.3 - 8.7 |
| 12 | ozone | 9.61 | 9.42 - 9.8 |
| 13• | surface & cloud IR | 10.35 | 10.1 - 10.6 |
| 14 | longwave IR window | 11.2 | 10.8 - 11.6 |
| 15 | dirty-window IR | 12.3 | 11.8 - 12.8 |
| 16 | carbon dioxide | 13.3 | 13.0 - 13.6 |
USA geostationary GOES-16 weather satellite has 16 imager channels (wavelength bands) for viewing the Earth system (Fig. 8.4). Some of the spectral bands were chosen specifically to look through different transmittance windows to “see” different atmospheric and cloud features. These channels are summarized in Table 8-2. Three bands traditionally used by forecasters are visible, IR, and water vapor.
Imager channels for the European Meteosat-10 are listed in Table 8-3. This satellite has 12 channels. Included are more visible channels to better discern colors.
| Table 8-3. Imager channels on European MSG-3 (Meteosat-10) weather satellite. VIS = visible. NIR = near infrared. IR = infrared. WV = water vapor. | |||
| Channel # | Name | Center Wavelength (µm) | Wavelength Range (µm) |
|---|---|---|---|
| 1 | VIS 0.6 (visible orange) | 0.635 | 0.56 - 0.71 |
| 2 | VIS 0.8 (deep red) | 0.81 | 0.74 - 0.88 |
| 3 | NIR 1.6 (near IR) | 1.64 | 1.50 - 1.78 |
| 4 | IR 3.9 | 3.90 | 3.48 - 4.36 |
| 5 | WV 6.2 (water vapor: high trop. | 6.25 | 5.35 - 7.15 |
| 6 | WV 7.3 (water vapor: mid-trop.) | 7.35 | 6.85 - 7.85 |
| 7 | IR 8.7 | 8.70 | 8.30 - 9.10 |
| 8 | IR 9.7 (ozone) | 9.66 | 9.38 - 9.94 |
| 9 | IR 10.8 | 10.80 | 9.80 - 11.8 |
| 10 | IR 12.0 | 12.00 | 11.0 - 13.0 |
| 11 | IR 13.4 (hightroposphere) | 13.40 | 12.4 - 14.4 |
| 12 | HRV (highresolution visible) | broadband | 0.4 - 1.1 |
8.2.2.1. Visible
Visible satellite images (GOES-16 channels 1 and 2) show what you could see with your eyes if you were up in space. All cloud tops look white during daytime, because of the reflected sunlight. In cloudfree regions the Earth’s surface is visible. At night, special low-light visible-channel imagers on some satellites can see city lights and moonlit clouds. Without this feature, visible images are useless at night.
8.2.2.2. Infrared (IR)
Infrared satellite images (GOES channel 13) use long wavelengths in a transmittance window, and can clearly see through the atmosphere to the surface or the highest cloud top. There is very little solar energy at this wavelength to be reflected from the Earth system to the satellite; hence, the satellite sees mostly emissions from the Earth or clouds. The advantage of this channel is it is useful both day and night, because the Earth never cools to absolute zero at night, and thus emits IR radiation day and night.
Images made in this channel are normally greyshaded such that colder temperatures look whiter, and warmer looks darker. Recall that standard-atmosphere temperature decreases as height increases in the troposphere (Chapter 1). Thus, white-colored clouds in this image indicate high clouds (cirrus, thunderstorm anvils, etc.), and darker grey clouds are low clouds (stratus, fog tops, etc.) Medium grey shading implies middle clouds (altostratus, etc.).
Fig. 8.15 demonstrates the principles behind this IR shading. At any one spot in the field of view, (a) a radiance L is measured by the satellite radiometer — for example: 7.6 W·m–2·µm–1·sr–1, as shown by the dashed line. The picture element (pixel) in the image that corresponds to this location is shaded darker (b) for greater L values, mimicking photographic film that becomes darker when exposed to more light. Not knowing the emissivity of the emitting object viewed at this spot, you can (c) assume a blackbody, and then use the Planck curve (d) for this IR channel to infer (e) brightness temperature TB ( = 283 K in this example). But for any normal temperature profile in the troposphere, such as the standard atmosphere (f), warmer temperatures are usually (g) closer to the ground (z = 0.9 km in this example).
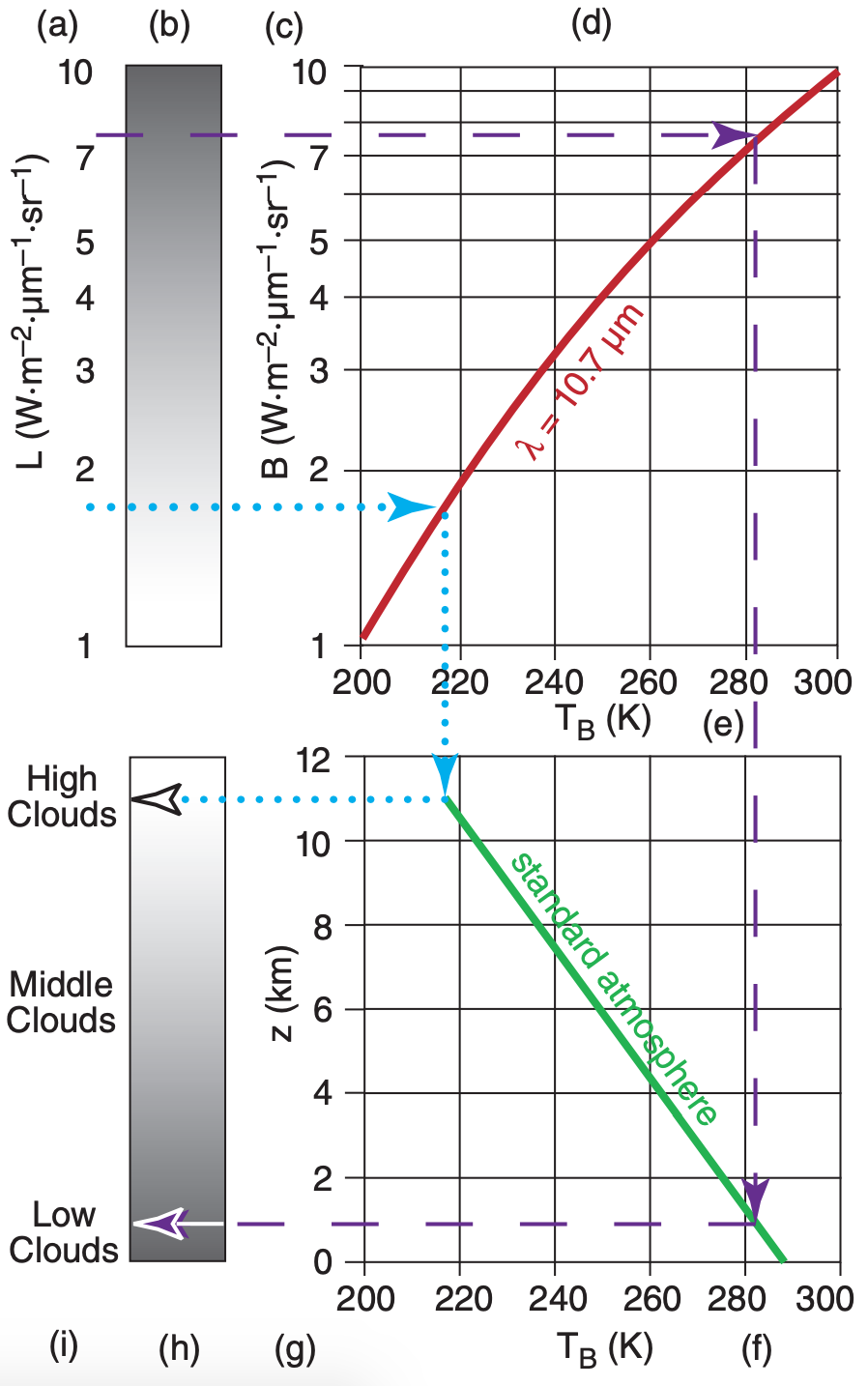
The net result for this IR window channel is that the darker shading (from Fig. 8.15b, redrawn in h) corresponds to lower clouds (i). Similarly, following the dotted curve, lesser values of observed radiance correspond to colder temperatures and higher clouds, and are shown as whiter pixels.
8.2.2.3. Water-vapor (WV)
Water-vapor images are obtained by picking a wavelength (channel 3) that is NOT in a window. In this part of the spectrum, water (as vapor, liquid, or ice) in the atmosphere can absorb radiation. If little water is present in the mid to upper troposphere (Fig. 8.8b), then most of the IR radiation from the Earth can reach the satellite. The warm brightness temperature associated with emissions from the Earth’s surface is displayed as dark grey in a water-vapor satellite image — indicating drier air aloft.
For higher concentrations of water in air, most of the surface emissions do not reach the satellite because they are absorbed by the water in the mid to upper troposphere. Kirchhoff’s law tells us that this atmospheric layer is also an effective emitter. The colder brightness temperatures associated with strong emissions from this cold layer of air are displayed as light grey — indicating moist air aloft.
Water-vapor images are useful because: (1) they provide data day and night; (2) animations of image sequences show the movement of the air, regardless of whether clouds are present or not; and (3) they give average conditions over a thick layer in the upper troposphere. Because of item (2), pattern recognition programs can estimate average winds in the upper troposphere by tracking movement of blobs of humid air, with or without clouds being present.
8.2.2.4. Channel Usage
The various GOES-16 channels are designed for a variety of applications: (channel 1) daytime aerosol mapping over land, coastal water mapping; (2) daytime clouds and fog, insolation, winds; (3) daytime vegetation and burn scars, aerosols over water, winds; (4) daytime cirrus clouds; (5) daytime cloud-top hydrometeor phase and size, snow; (6) land use, particle size, vegetation, snow; (7) surface and clouds, fog at night, fire, winds; (8-10) water vapor at high (8), mid (9) and low (10) altitudes in the troposphere; (11) total water, cloud phase, dust, SO2, rainfall; (12) total ozone, turbulence, winds; (13) surface and cloud features; (14) images, sea-surface temperature, cloud-top temperature, rain; (15) volcanic ash, total water, sea surface temperature; and (16) air temperature, cloud coverage and heights.
8.2.3. Image Examples & Interpretation
Figures 8.16a-c show visible (Vis), infrared (IR) and water vapor (WV) images of the same scene. You can more successfully interpret cloud type when you use and compare all three of these image channels. The letters below refer to labels added to the images. Extra labels on the images are used for a Sample Application and for homework exercises.


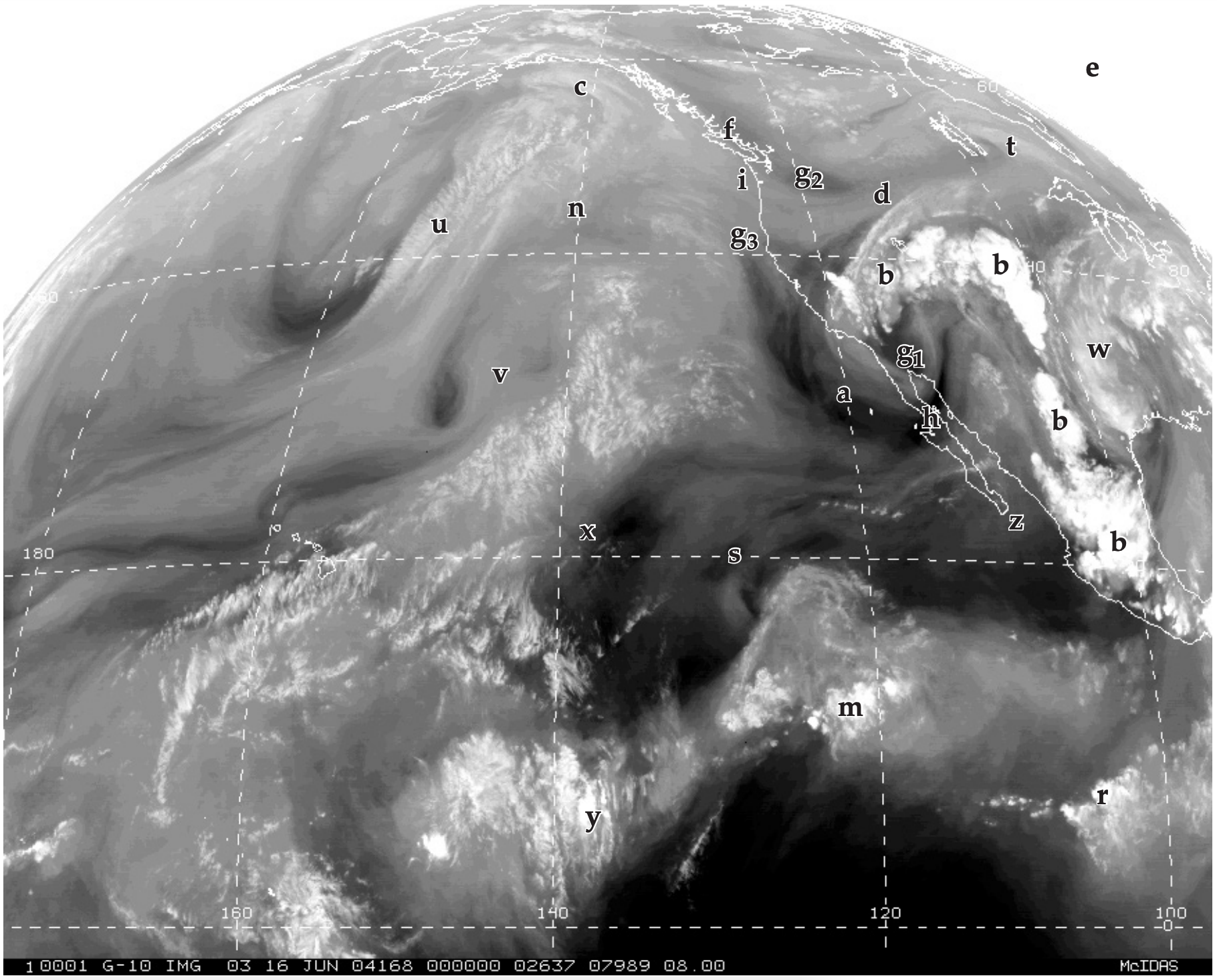
a. Fog or low stratus:
Vis: White, because it is a cloud.
IR: Medium to dark grey, because low, warm tops.
WV: Invisible, because not in upper troposphere. Instead, WV shows amount of moisture aloft.
b. Thunderstorms:
Vis: White, because it is a cloud.
IR: Bright white, because high, cold anvil top.
WV: Bright white, because copious amounts of water vapor, rain, and ice crystals fill the mid and upper troposphere. Often the IR and WV images are enhanced by adding color to the coldest temperatures and most-humid air, respectively, to help identify the strongest storms.
c. Cirrus, cirrostratus, or cirrocumulus:
Vis: White, because cloud, although can be light grey if cloud is thin enough to see ground through it.
IR: White, because high, cold cloud.
WV: Medium to light grey, because not a thick layer of moisture that is emitting radiation.
d. Mid-level cloud tops:
Could be either a layer of altostratus/altocumulus, or the tops of cumulus mediocris clouds.
Vis: White, because it is a cloud.
IR: Light grey, because mid-altitude, mediumtemperature.
WV: Medium grey. Some moisture in cloud, but not a thick enough layer in mid to upper troposphere to be brighter white.
e. Space:
Vis: Black (unless looking toward sun).
IR: White, because space is cold.
WV: White, because negligible emissions from space.
f. Snow-capped Mountains (not clouds):
Vis: White, because snow is white.
IR: Light grey, because snow is cold, but not as cold as high clouds or outer space.
WV: Maybe light grey, but almost invisible, because mountains are below the mid to upper troposphere. Instead, WV channel shows moisture aloft.
g. Land or Water Surfaces (not clouds):
g1 is in very hot desert southwest in summer, g2 is in arid plateau, and g3 is Pacific Ocean.
Vis: Medium to dark grey. Color or grey shade is that of the surface as viewed by eye.
IR: g1 is black, because very hot ground.
g2 is dark grey, because very warm.
g3 is light grey, because cool ocean.
WV: Light grey or invisible, because below mid to upper troposphere. Instead, sees moisture aloft.
h. Tropopause Fold or Dry Air Aloft:
Vis: Anything.
IR: Anything.
WV: Dark grey or black, because very dry air in the upper troposphere. Occurs during tropopause folds, because dry stratospheric air is mixed down.
i. High Humidities Aloft:
Vis: Anything.
Vis: Anything.
WV: Light grey. Often see meandering streams of light grey, which can indicate a jet stream. (Might be hard to see in this copy of a satellite image.)
“Image Interpretation” means the use of satellite images to determine weather features such as fronts, cyclones, thunderstorms and the global circulation. This is a very important part of manual weather forecasting. Whole books are devoted to the subject, and weather forecasters receive extensive training in it. In this book, overviews of image interpretation of cyclones, fronts, and thunderstorms are covered later, in the chapters on those topics.
However, for future reference, Fig. 8.16d shows my interpretation of the previous satellite photos. This particular interpretation shows only some of the larger-scale features. See the Fronts, Cyclones, and General Circ. chapters for symbol definitions.
Sample Application
Determine cloud type at locations “m” and “n” in satellite images 8.16a-c.
Find the Answer
Given: visible, IR, and water vapor images
Find: cloud type
m:
vis: White, therefore cloud, fog, or snow.
IR: White, thus high cloud top (cirrus or thunderstorm, but not fog or snow).
wv: White, thus copious moisture within thick cloud layer. Thus, not cirrus.
Conclusion: thunderstorm.
n:
vis: White or light grey, thus cloud, fog, or snow. (Snow cover is unlikely on unfrozen Pacific).
IR: Medium grey, roughly same color as ocean. Therefore warm, low cloud top.
wv: Medium grey (slightly darker than surround- ing regions), therefore slightly drier air aloft. But gives no clues regarding low clouds.
Conclusion: low clouds or fog.
Check: Difficult to check or confirm now. After you learn synoptics you can check if the cloud feature makes sense for the weather pattern that it is in.
Exposition: This is like detective work or like a medical diagnosis. Look at all the clues, and rule out the clouds that are not possible. Be careful and systematic. Use other info such as the shape of the cloud or its position relative to other clouds or relative to mountains or oceans. Interpreting satellite photos is somewhat of an art, so your skill will improve with practice.
8.2.4. Sounder
GOES-15 has a sounder radiometer with 19 channels. GOES-16 doesn’t need a separate sounder because the Advanced Baseline Imager (ABI) has sufficient image channels to allow sounding retrievals. The different wavelength channels (Table 8-2) have different weighting functions (Fig. 8.9) that peak at different altitudes, allowing us to retrieve a sounding (temperatures at different altitudes). We will examine the basics of this complex retrieval process.
There is a limit to our ability to retrieve sounding data, as summarized in two corollaries. Corollary 1 is given at right. To demonstrate it, we will start with a simple weighting function and then gradually add more realism in the subsequent illustrations.
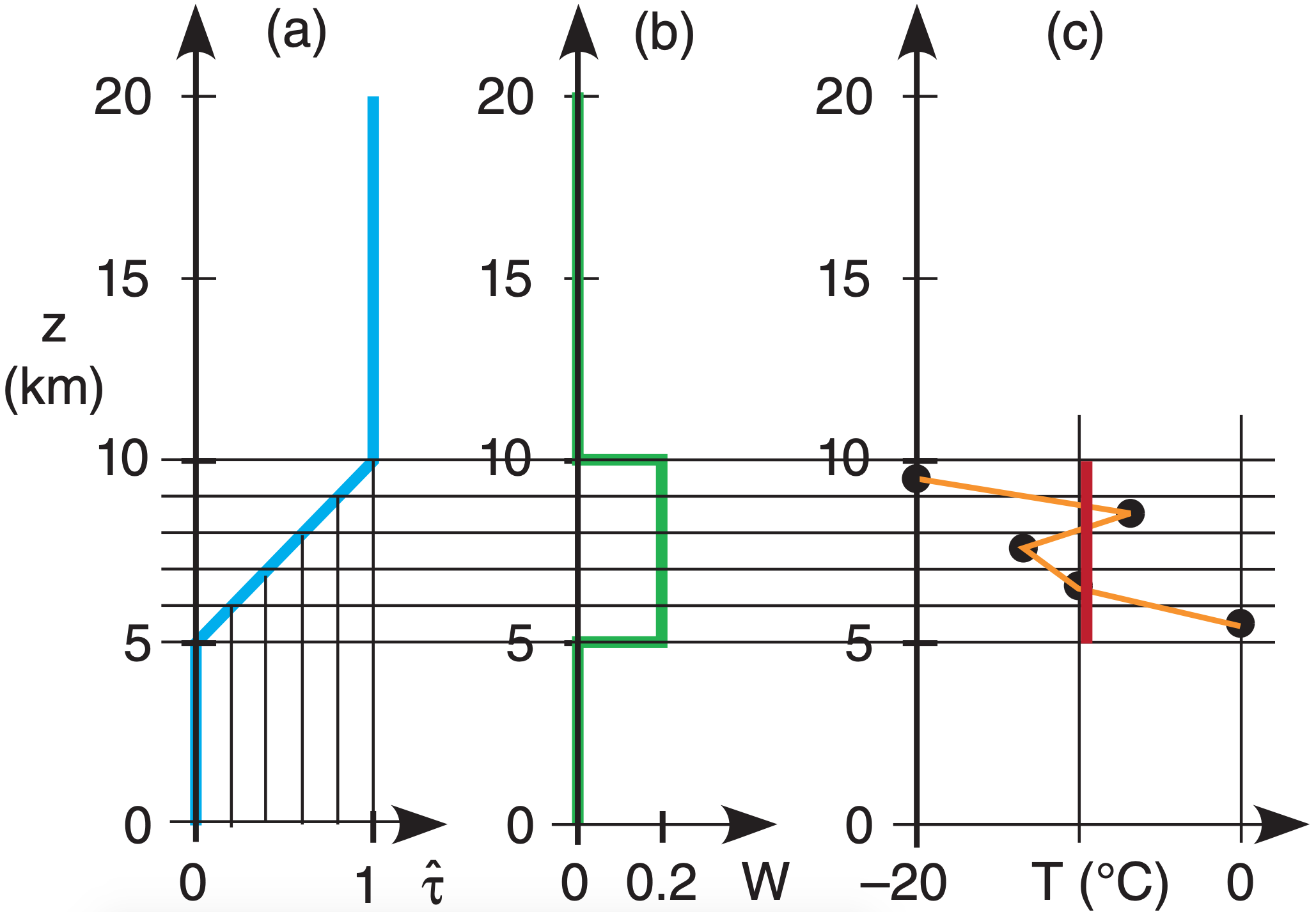
Consider the previous idealized transmittance profile (Fig. 8.7), but now divide the portion between z = 5 and 10 km into 5 equal layers. As shown in Fig. 8.17a, the change in transmittance across each small layer is ∆ \(\ \hat{\tau}\) = 0.2 (dimensionless); hence, the weight (Fig. 8.17b) for each layer is also W = 0.2 . Assume that this is a crude approximation to sounder channel 3, with a central wavelength of λ = 14.0 µm.
Suppose the “actual” temperature of each layer, from the top down, is T = –20, –6, –14, –10, and 0°C, as illustrated by the data points and thin line in Fig. 8.17c. (Ignore the portions of the sounding below 5 km and above 10 km, because this weighting function cannot “see” anything at those altitudes.
Using Planck’s Law (eq. 8.1), find the blackbody radiance from each layer from the top down: B = 3.88, 4.82, 4.27, 4.54, and 5.25 W·m–2·µm–1·sr–1. Weight each by W = 0.2 and then sum according to the radiative transfer eq. (8.5) to compute the weighted average. This gives the radiance observed at the satellite: L = 4.55 W·m–2·µm–1·sr–1. The surface (skin) term in eq. (8.5) was neglected because the transmittance from the surface is zero, so no surface information reaches the satellite for this idealized situation.
This satellite-observed radiance is communicated to ground stations, where automatic computer programs retrieve the temperature using eq. (8.2). When we do that, we find TB = 263.18 K , or T = –9.82°C. This is plotted as the thick line in Fig. 8.17c.
Detailed temperature-sounding structure is not retrieved by satellite, because the retrieval can give only one piece of temperature data per weighting function. Vertically broad weighting functions tend to cause significant smoothing of the retrieved temperature sounding.
Scatterometer sensors on satellites can detect capillary waves on the ocean, allowing near-surface wind speeds to be estimated. Passive and active Special Sensor Microwave Imagers (SSM/I) can retrieve precipitation and precipitable water over the ocean. Combining a series of observations while a satellite moves allows small on-board antennas to act larger, such as via synthetic aperture radar (SAR).
GOES-16 has a Geostationary Lightning Mapper (GLM) that has an optical transient detector to observe lightning flashes. When a lightning discharge happens, it excites oxygen atoms in the air, which then emit near IR radiation at 0.7774 µm wavelength. The GLM detector is tuned to this wavelength. This emission can be observed both day and night.
Retrieval Corollary 1: The sounder can retrieve (at most) one piece of temperature data per channel. The temperature it gives for that channel is the average brightness temperature weighted over the depth of the weighting function.
8.2.4.1. Illustration of Retrieval Corollary 1 (Non-overlapping Weighting Functions)
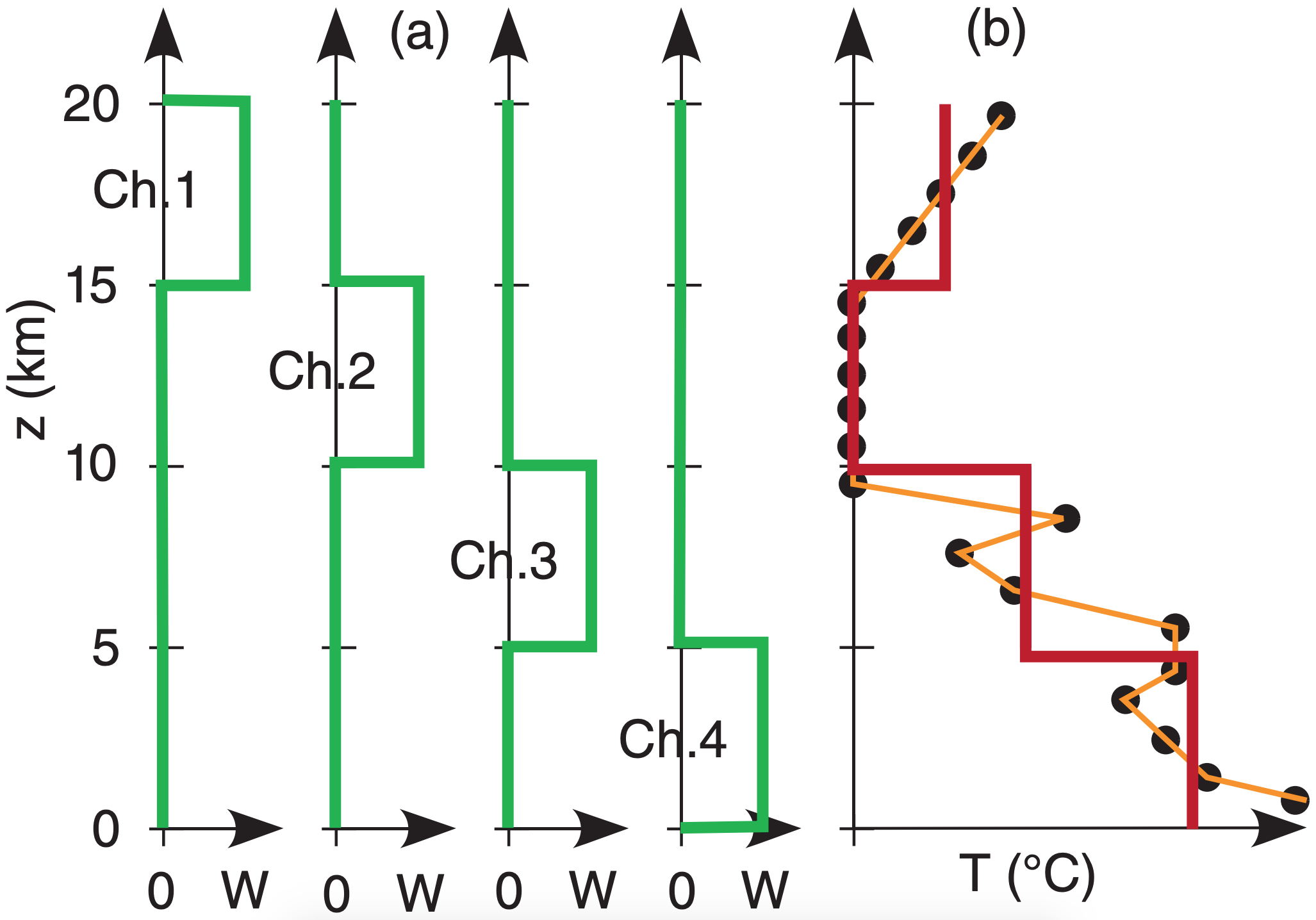
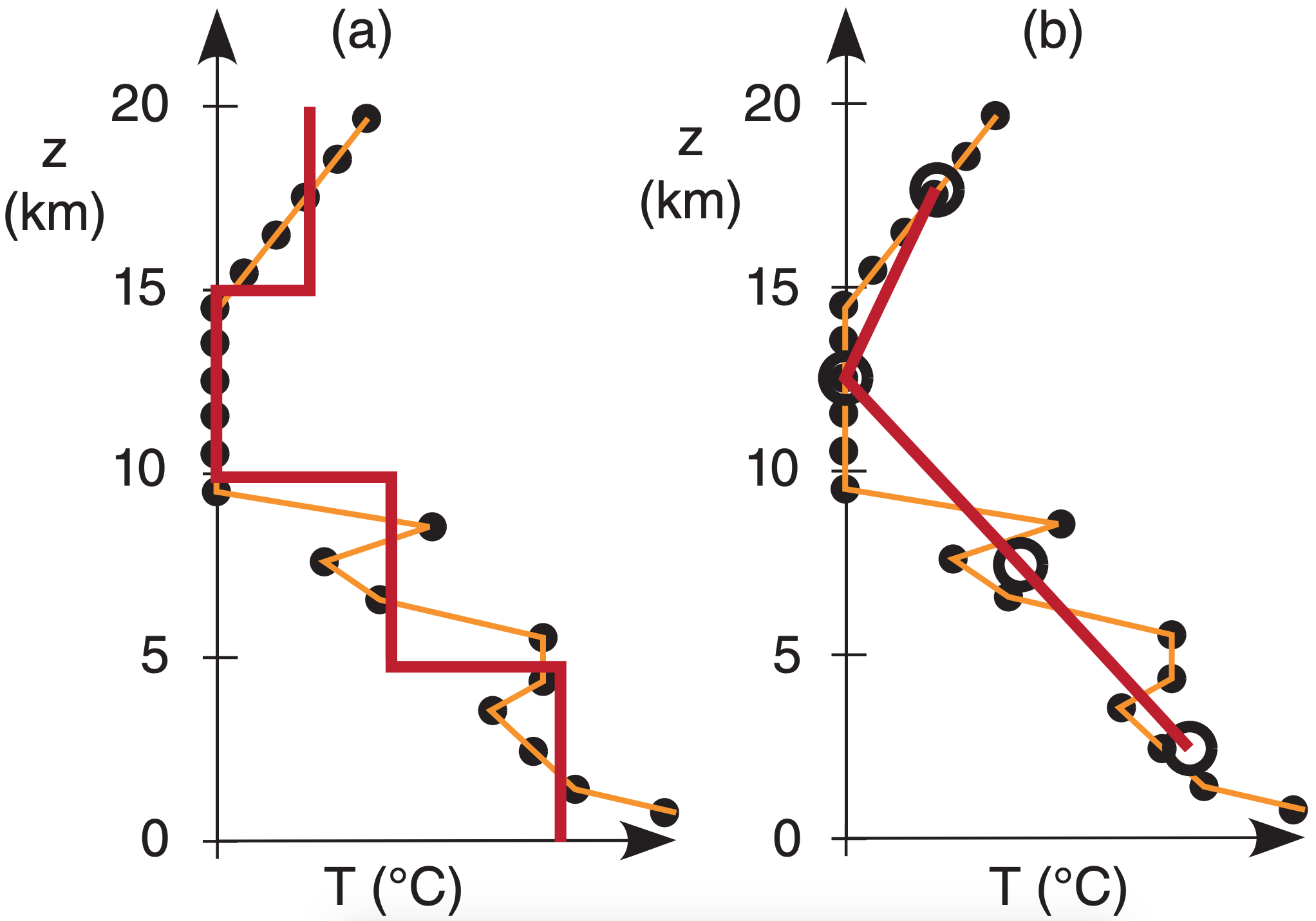
Consider a slightly more realistic illustration of a perfect (idealized) case where the weighting functions do not overlap vertically between different channels (Fig. 8.18a). The relationship between actual temperatures (thin line) and the resulting temperature retrievals are sketched. Namely, the weighting functions are independent of each other, allowing the four channels to retrieve four independent temperatures, as plotted by the thick line (Fig. 8.18b). The thick line is the retrieved sounding.
Instead of plotting the retrieved sounding as a sequence of vertical line segments as shown in Fig. 8.19a, it is often plotted as data points. For our four independent channels, we would get four data points (large, open circles), and the resulting sounding line is drawn by connecting the circles (Fig. 8.19b). The retrieved sounding (thick line in Fig. 8.19b) does a good job of capturing the gross-features of the temperature profile, but misses the fine details such as sharp temperature inversions.
8.2.4.2. Illustration of Retrieval Corollary 2 (Overlapping Weighting Functions)
With non-overlapping weighting functions, the sounding-retrieval process was easy. For more realistic overlapping weighting functions, it becomes very difficult, as summarized in Retrieval Corollary 2, given in the left column.
We can first study this as a forward problem, where we pretend we already know the temperature profile and want to find the radiances that the satellite would see. This approach is called an Observing System Simulation Experiment (OSSE), used by instrument designers to help anticipate the radiances arriving at the satellite, so that they can fix problems before the satellite is launched. We anticipate that the radiance received in one channel depends on the temperatures at many heights. Easy!
Later, we will approach this more realistically; i.e., as an inverse problem where we have satellite-measured radiances and want to determine atmospheric temperatures. The inverse problem for overlapping weighting functions requires us to solve a set of coupled nonlinear equations. Nasty!
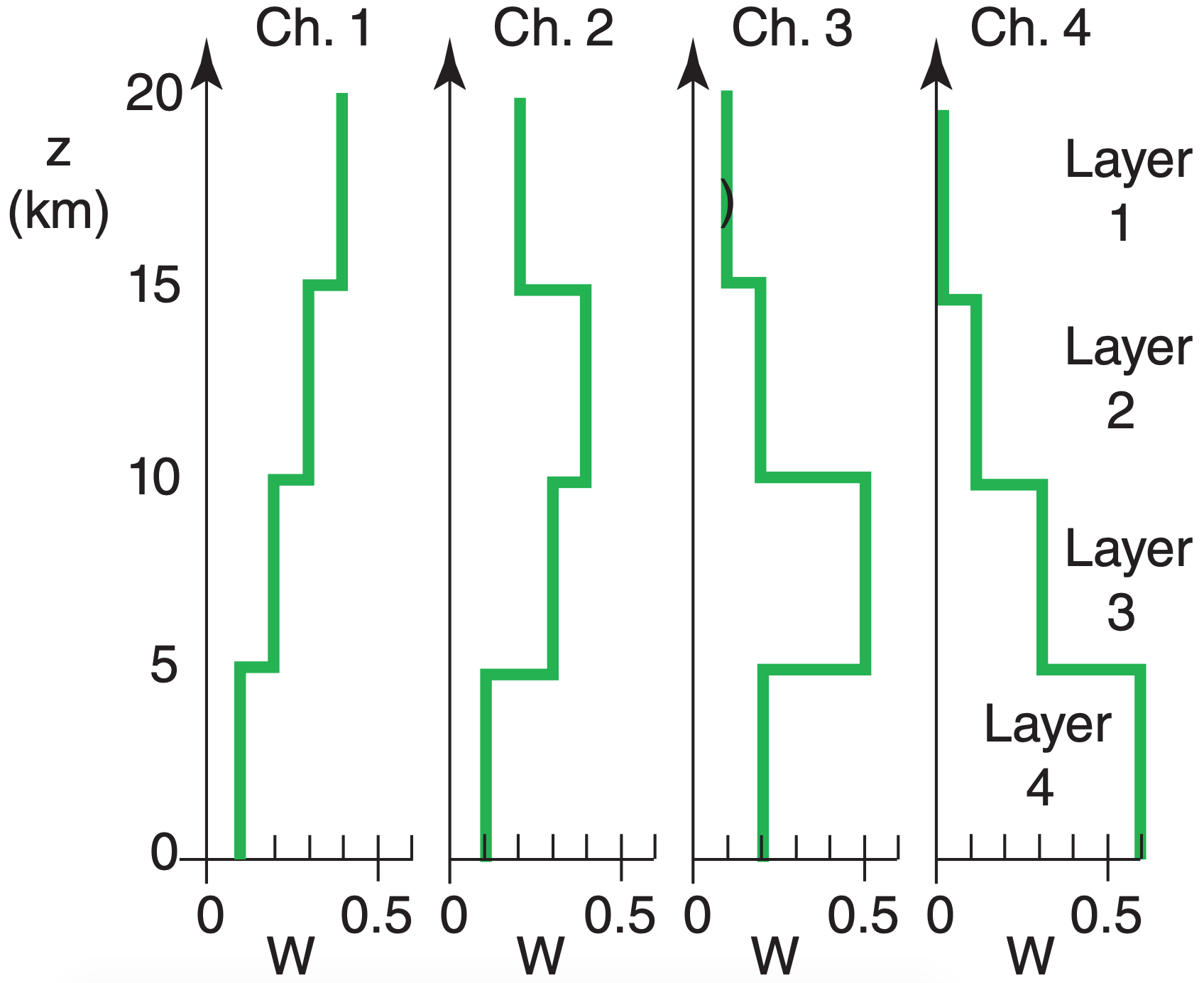
To illustrate the forward problem, suppose that idealized weighting functions of Fig. 8.20 and Table 8-4 approximate GOES-15 weighting functions for sounder channels 1 – 4. For any one channel, the sum of the weights equals one, as you can check from the data in the figure. Each weighting function peaks at a different height. For simplicity, look at only the atmospheric contribution to the radiances and ignore the surface (skin) term.
Retrieval Corollary 2: If weighting functions from different channels have significant overlap in altitude and have similar shapes, then they do not provide independent observations of the atmosphere. For this situation, if there are also measurement errors in the radiances or the weighting functions, then the sounding can retrieve fewer than one piece of temperature data per sounder channel. (See the “Higher Math” box later in this section for a demonstration.)
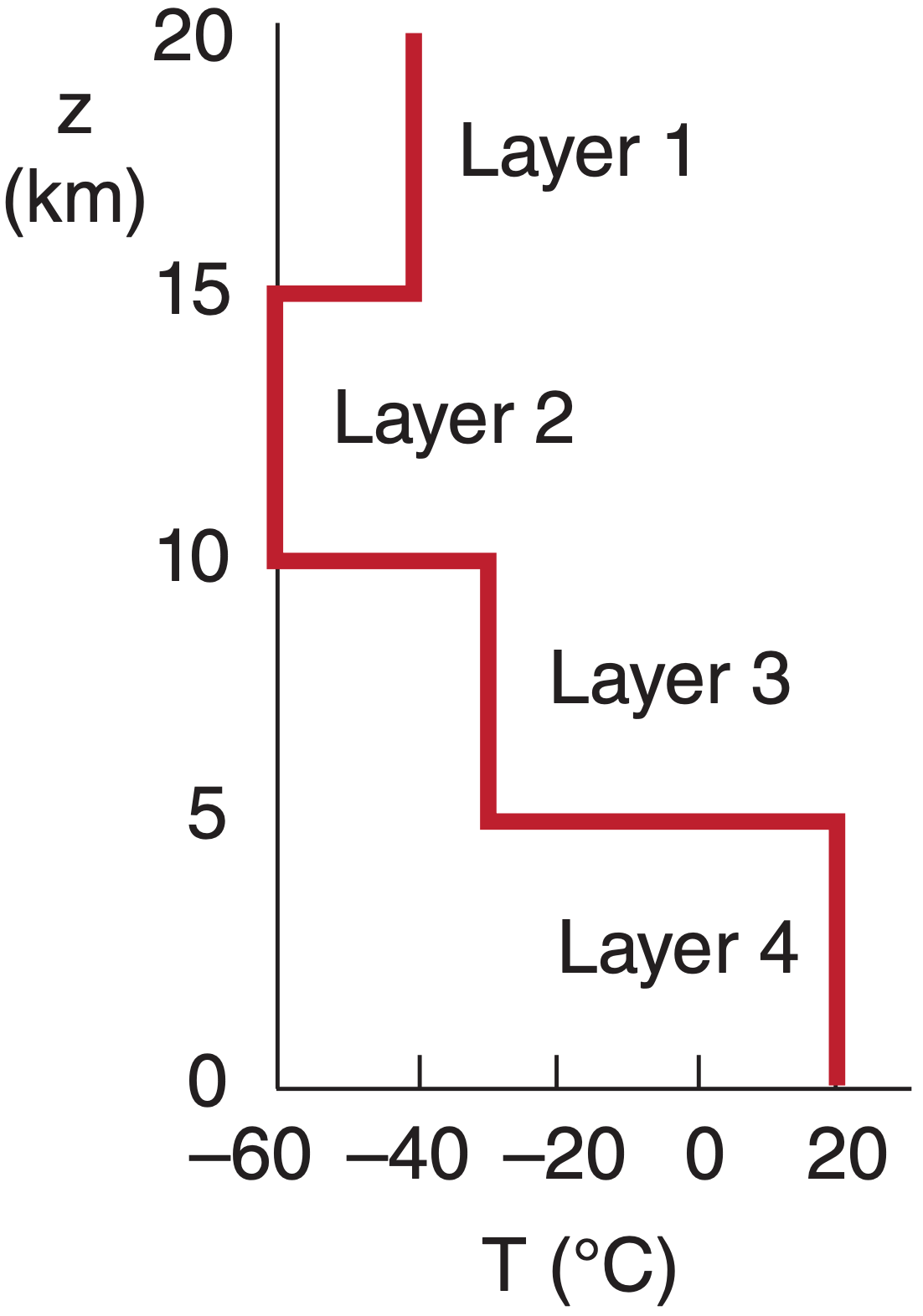
For this forward example, suppose the temperatures for each layer (from the top down) are T = –40, –60, –30, and +20°C, as plotted in Fig. 8.21. Namely, we are using a coarse-resolution T profile, because we already know from Corollary 1 that retrieval methods cannot resolve anything finer anyway.
| Table 8-4. Idealized sounder weights W λ , j . | |||||
| Vector | Channel (λ) | Layer in Atmosphere (j) | |||
|---|---|---|---|---|---|
| 1 (top) | 2 | 3 | 4 (bottom) | ||
| A | 1 | 0.4 | 0.3 | 0.2 | 0.1 |
| B | 2 | 0.2 | 0.4 | 0.3 | 0.1 |
| C | 3 | 0.1 | 0.2 | 0.5 | 0.2 |
| D | 4 | 0 | 0.1 | 0.3 | 0.6 |
For each channel, we can write the radiative transfer equation (8.5). To simplify these equations, use λ = 1, 2, 3, 4 to index the wavelengths of sounder channels 1, 2, 3, 4. Also, use j = 1, 2, 3, 4 to index the four layers of our simplified atmosphere, from the top down. The radiative transfer equation for our simple 4-layer atmosphere, without the skin term, is:
\(\ \begin{align} L_{\lambda}=\sum_{j=1}^{4} B_{\lambda}\left(T_{j}\right) \cdot W_{\lambda, j}\tag{8.9}\end{align}\)
After expanding the sum, this equation can be written for each separate channel as:
\(\ \begin{align} L_{1}=B_{1}\left(T_{1}\right) \cdot W_{1,1}+B_{1}\left(T_{2}\right) \cdot W_{1,2}+B_{1}\left(T_{3}\right) \cdot W_{1,3}+B_{1}\left(T_{4}\right) \cdot W_{1,4} \tag{8.10a}\end{align}\)
\(\ \begin{align}L_{2}=B_{2}\left(T_{1}\right) \cdot W_{2,1}+B_{2}\left(\mathrm{T}_{2}\right) \cdot W_{2,2}+B_{2}\left(T_{3}\right) \cdot W_{2,3}+B_{2}\left(T_{4}\right) \cdot W_{2,4}\tag{8.10b}\end{align}\)
\(\ \begin{align} L_{3}=\mathrm{B}_{3}\left(T_{1}\right) \cdot W_{3,1}+B_{3}\left(T_{2}\right) \cdot W_{3,2}+B_{3}\left(T_{3}\right) \cdot W_{3,3}+B_{3}\left(T_{4}\right) \cdot W_{3,4}\tag{8.10c}\end{align}\)
\(\ \begin{align}L_{4}=
B_{4}\left(T_{1}\right) \cdot W_{4,1}+B_{4}\left(T_{2}\right) \cdot W_{4,2}+B_{4}\left(T_{3}\right) \cdot W_{4,3}+B_{4}\left(T_{4}\right) \cdot W_{4,4}\tag{8.10d}\end{align}\)
j: layer 1 \(\quad\) layer 2 \(\quad\) layer 3 \(\quad\) layer 4
| Table 8-5. Solution of the forward radiative transfer equation for the 4-layer illustrative atmosphere. These wavelengths λ correspond to GOES-15 sounder channels 1-4. | ||
| Channel | λ (µm) | L ( W·m–2 ·µm–1 ·sr–1 ) |
|---|---|---|
| 1 | 14.7 | 2.85 |
| 2 | 14.4 | 2.87 |
| 3 | 14.0 | 3.64 |
| 4 | 13.7 | 5.40 |
Because of the large vertical spread of the weights, the radiance in each channel depends on the temperature at many levels, NOT just the one level at the peak weight value. But the radiative transfer equations are easy to solve; namely, given T and W, it is straightforward to calculate the radiances L, because we need only solve one equation at a time. I did this on a spreadsheet — the resulting radiances for each channel are in Table 8-5.
Now consider the more realistic inverse problem. To find the temperature T for each layer, knowing the radiance L from each sounder channel, you must solve the whole set of coupled equations (8.10ad). These eqs. are nonlinear with respect to temperature, due to the Planck function B. The number of equations equals the number of sounder channels. The number of terms in each equation depends on how finely discretized are the sounder profiles from Fig. 8.9, which is related to the number of retrieval altitudes. From Retrieval Corollary 1 there is little value in retrieving more altitudes than the number of sounder channels. For example, the GOES-16 satellite has 16 channels; hence, we need to solve a coupled set of 16 equations, each with 16 nonlinear terms.
Solving this large set of coupled nonlinear equations is tricky; many different methods are used by government forecast centers and satellite institutes. Here is a simple, unsophisticated, brute-force approach that you can solve on a spreadsheet, which gives an approximate solution:
Start with an initial guess for the temperature of each layer. The better the first guess, the quicker you will converge toward the best answer. Use those temperatures to solve the much easier forward problem; namely, calculate the radiances Lλ from each eq. (8.10) separately. Calculate the squared error ( Lλ calc – Lλ obs )2 between the calculated radiances and the observed radiances from satellite for each channel, and then sum the errors to get an overall measure of the quality of the guessed temperature sounding.
Next, try to reduce the overall error by modifying the temperature guesses. For example, vary the guessed temperature for only one atmospheric layer, until you find the temperature that gives the least total error. Then do the same for the next height, and continue doing this for all heights. Then repeat the whole process, from first height to last height, always seeking the minimum error. Keep repeating these steps (i.e., keep iterating), until the total error is either zero, or small enough (considering errors in the measured radiances).
Some of the difficulties in sounding retrievals are listed in the Info Box below. In spite of these difficulties, satellite data make an important positive contribution to weather-forecast quality. Modern numerical weather prediction can assimilate radiances directly, without needed a sounding retrieval.
| Table 8-6. Approximate solution to the Sample Applic. inverse problem. T (°C) is air temperature. L (W·m–2·µm–1·sr–1) is radiance. Error = L(obs) – L(guess). | ||||
| Height: | 1 (top) | 2 | 3 | 4 (bot.) |
|---|---|---|---|---|
| T (initial guess) | –20 | –20 | –20 | –20 |
| T (1st iteration) | –32.9 | –42.9 | –43.3 | +2.5 |
| T (final guess) | –45 | –50.1 | –33.6 | +20.1 |
| Channel: | 1 | 2 | 3 | 4 |
| L (obs) | 2.85 | 2.87 | 3.64 | 5.40 |
| L (from T initial guess) | 3.70 | 3.78 | 3.88 | 3.95 |
| error2 | 0.7189 | 0.8334 | 0.0591 | 2.114 |
| sum of error2 | 3.7255 | |||
| L (from T final guess) | 2.84 | 2.93 | 3.60 | 5.39 |
| error2 | 0.00009 | 0.00367 | 0.00155 | 0.00019 |
| sum of error2 | 0.0055 | |||
Sample Application
Given a 4-channel sounder with weighting functions in Fig. 8.20 & Table 8-4, having the corresponding satellite-observed radiances of: L1 = 2.85, L2 = 2.87, L3 = 3.64, & L4 = 5.4 W·m–2·µm–1·sr–1. Retrieve the temperature sounding.
Find the Answer
Given: L(obs) above; weights W from Table 8-4.
Find: Temperatures T1 to T4 (K), where ()1 is top layer.
I did this manually by trial and error on a spreadsheet — a bit tedious, but it worked.
- First, guess a starting sounding of T(guess) = –20°C everywhere (= 253K). See Table 8-6.
- Use eqs. (8.10) to compute radiances L(guess) for each channel.
- For Ch.1: error2 1 = (L1 guess – L1 obs)2 ; etc. for Ch.2-4.
- Compute Sum of error2 = error2 1 + error2 2 + etc.
This initial total error was very large ( = 3.7255 W·m–2·µm–1·sr–1).
- Experiment with different values of T4 (temperature of layer 4) to find the “best” value that gives the least Sum of error2 so far. Then, keeping this “best” T4 value, experiment with T3 , finding its best value. Proceed similarly for layers 2 & 1. This completes iteration 1, as shown in Table 8-6.
- Keeping the best T1 through T3, experiment with T4 again — you will find a different “best” value. Then do layers 3, 2, & 1 in succession. This ends iteration 2.
- Keep iterating for layers 4, 3, 2, 1. Boring. But each time, the Sum of error2 becomes less and less.
As my error became small, I eventually got tired and stopped iterating. The answer is T(final guess) in Table 8-6.
Check: The actual T is given in Fig. 8.21, & listed here:
| Height: | 1 (top) | 2 | 3 | 4 (bot.) |
|---|---|---|---|---|
| T (actual) | –40 | –60 | –30 | +20 |
| T (final guess) | –45 | –50.1 | –33.6 | +20.1 |
Exposition: Not a perfect answer, which we know only because this exercise was contrived from an earlier illustration where we knew the actual temperature.
Why was it not perfect? It was very difficult to get the temperatures for layers 1 and 2 to converge to a stable solution. Quite a wide range of temperature values for these layers gave virtually the same error, so it was difficult to find the best temperatures. This is partly related to the close similarity in weighting functions for Channels 1 and 2, and the fact that they had large spread over height with no strong peak in any one layer. The radiances from these two channels are not independent of each other, resulting in a solution that is almost singular (not well behaved in a mathematical sense; not allowing a solution).
These difficulties are typical. See the “Info Box” on the next page.
- Radiance is an average from a deep layer, often overlapping with other layers.
- Radiance observations (in different channels) are not independent of each other
- It is difficult to separate the effects of temperature and water-vapor variations in radiance signal.
- There is not a unique relationship between the spectrum of outgoing radiance and atmospheric temperature and humidity profiles.
- Temperatures are nonlinearly buried within the Planck function (but make linear approximations).
- Radiance observations have errors caused by instrument errors, sampling errors, interference by clouds, and errors in the estimation of the weighting functions.
- Because of all these factors, there are an infinite number of temperature profiles that all satisfy the observed radiances within their error bars. Thus, statistical estimates must be used.
- To help pick the best profile, a good first guess and good boundary conditions are critical. (Retrieval Corollary 3: The retrieved profile looks more like the first guess than like reality.)
- Satellite-retrieved soundings are most useful in regions (such as over the oceans) lacking other in-situ observations, but in such regions it is difficult to provide a good first guess. Often numerical weather forecasts are used to estimate the first guess, but such forecasts usually deviate significantly from reality over ocean data-voids.
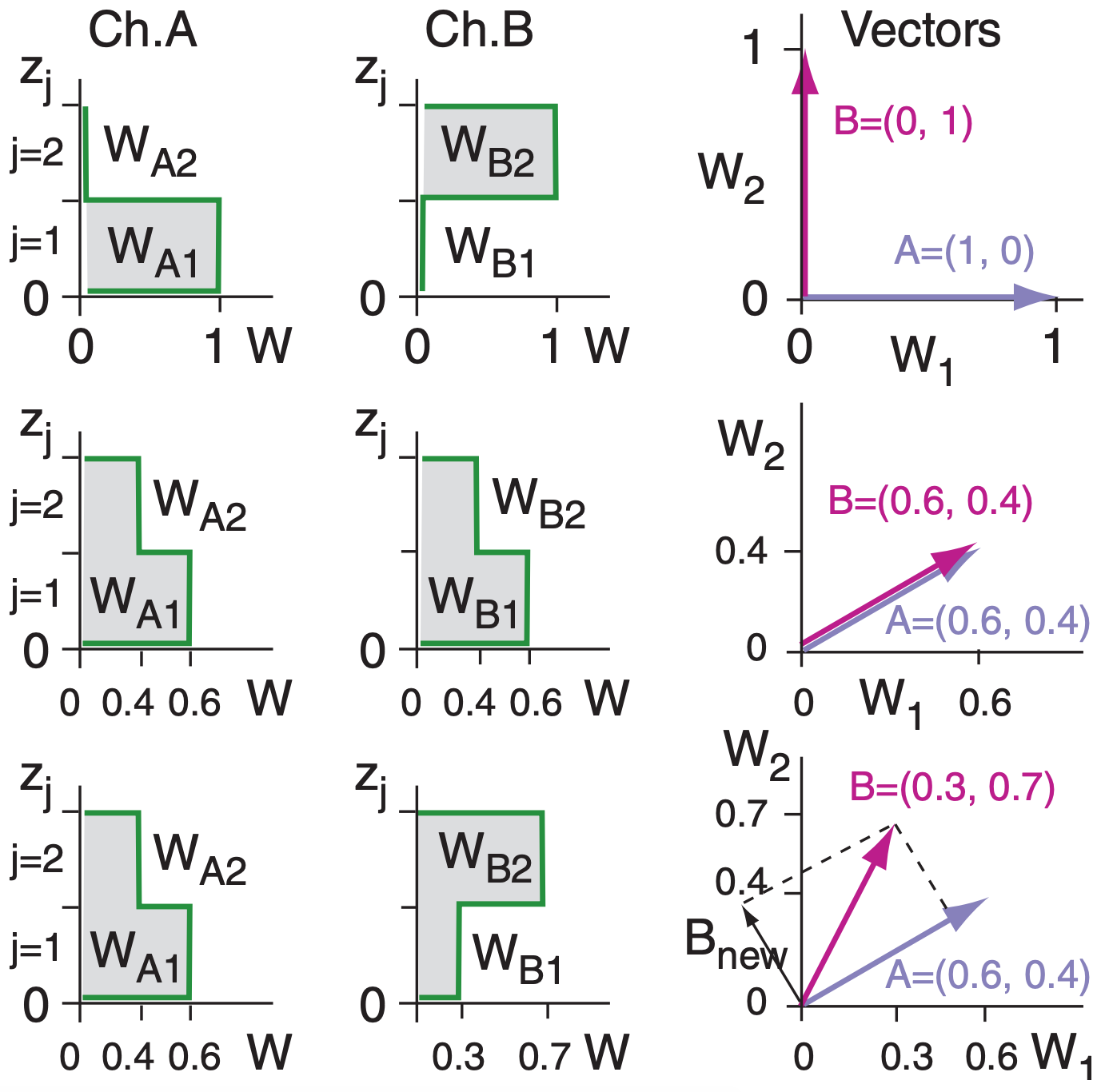
By representing weighting functions as vectors, inner (dot •) products show how much information from one vector is contained in (projected onto) the other vectors. This helps demonstrate satellite Retrieval Corollary 2: The amount of retrieved info can be less than the number of weighting functions.
To illustrate, consider a 2-layer atmosphere and let each height represent an orthogonal axis in 2-D space. The discrete weight values at each height within any one weighting function give corresponding coordinates for that vector in the 2-D space.
For example, row 1 of the Fig. at right shows weighting functions for two channels, A and B, which are represented as vectors in the last Fig. of that row. For this special case of non-overlapping weighting functions, A and B give completely independent pieces of info, as indicated by the orthogonal vectors. The total information value is 2.
Row 2 of the Fig. illustrates two identical weighting functions. Their vector representations perfectly coincide in the 2-D space. While the one weighting function gives us information, the second function tells us nothing new. Thus, total info value is 1.
Row 3 of the Fig. shows two different, but broadly overlapping, weighting functions. When plotted in vector space, we see that much of B projects onto A. Namely, much of B tells us nothing new. The only new contribution from vector B is the component that is orthogonal to A. For this example, only 30% of B gives new info (Bnew); therefore, the total info value is 1.3 ( = 1.0 from A + 0.3 from B).
In a sum-of-squares sense, the fraction of vector B = (WB1, WB2, WB3, ...) that is NOT explained by (i.e., not projected onto) vector A = (WA1, WA2, WA3, ...) is:
\(\ \begin{align} f=1-\frac{(A \bullet B)^{2}}{|A|^{2}|B|^{2}}=1-\frac{\left(\Sigma_{j} W_{A, j} W_{B, j}\right)^{2}}{\left(\Sigma_{j} W_{A, j}^{2}\right)\left(\Sigma_{j} W_{B, j}^{2}\right)}\tag{8.11}\end{align}\)
For higher-order vector spaces, we can use (8.11) to successively find the fraction of vector C that provides new info; namely, the portion of C that is orthogonal both to A and to the new-info part of B.
The vector representing the new-info part of B (the portion of B not projecting on A) is:
\(\ \begin{align} B_{n e w}=B_{\perp A}=B-\frac{(A \bullet B)}{|A|^{2}} A\tag{8.12}\end{align}\)
Using this info projection method on the weights of Fig. 8.20 (with vectors A to D identified in Table 8-4) gives: A: 1 , Bnew: 0.19 , Cadditional contrib. to Bnew = 0.267, Cnew = 0.258, Dcontrib. to Bnew = 0.115 , Dcontrib. to Cnew = 0.303 , Dnew = 0.419 .
The total info value sums to 2.55. Thus, the 4 weighting functions give fewer than 4 independent pieces of info about the temperature profile.