9.5: How is the horizontal divergence/convergence related to vertical motion?
- Page ID
- 3408
Credit: Unisys
Our goal here is to relate horizontal convergence and divergence to vertical motion. If vertical motion is upward, then the uplifted air will cool, clouds will form, and it might rain or snow. If vertical motion is downward, then the downwelling air will warm by adiabatic descent, clouds will evaporate, and it will become clear.
To find out what will happen, we need to go back to a fundamental law of mass conservation, which we will derive in detail in Lesson 10. Here we simply quote the result:
\[\frac{1}{\rho} \frac{D \rho}{D t}+\vec{\nabla} \bullet \vec{U}=0\]
where ρρ is the density and D/Dt is the total derivative.
For divergence, \(\vec{\nabla} \bullet \vec{U}>0\), volume decreases and density must increase to conserve mass.
However, to good approximation, density does not change with time for any given horizontal surface. Sure, density decreases exponentially with height, but for each height level, the density at that level is fairly constant.
So, to a good approximation:
\[\vec{\nabla} \bullet \vec{U}=0\]
and because we can separate out the horizontal and vertical components of divergence:
\[\vec{\nabla} \bullet \vec{U}=\vec{\nabla}_{H} \bullet \vec{U}_{H}+\frac{\partial w}{\partial z}\]
we see that:
\[\vec{\nabla}_{H} \bullet \vec{U}_{H}+\frac{\partial w}{\partial z}=0, \quad\) or \(\quad \frac{\partial w}{\partial z}=-\vec{\nabla}_{H} \bullet \vec{U}_{H}\]
Thus, horizontal divergence is compensated by vertical convergence and horizontal convergence is compensated by vertical divergence.
\[\vec{\nabla}_{H} \bullet \vec{U}_{H}>0 \quad\) means \(\quad \frac{\partial w}{\partial z}<0\]
Horizontal divergence gives a decrease in vertical velocity with height.
\[\vec{\nabla}_{H} \bullet \vec{U}_{H}<0 \quad\) means \(\quad \frac{\partial w}{\partial z}>0\]
Horizontal convergence gives an increase in vertical velocity with height.
Now, in the troposphere, the vertical velocity is close to zero (w ~ 0) at two altitudes. The first is Earth’s surface, which forms a solid boundary that stops the vertical wind. The second is the tropopause, above which the rapid increase in stratospheric potential temperature strongly inhibits vertical motion from the troposphere (see two figures below), so much so, that we can say that the vertical wind must be ~ 0 at the tropopause.
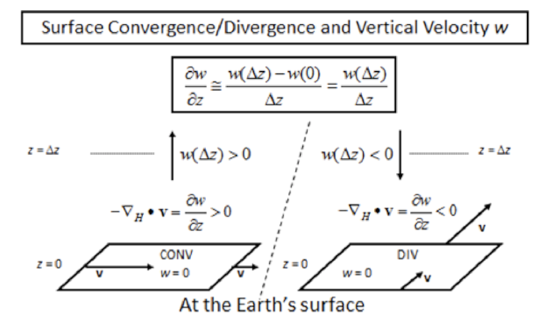
Credit: H.N. Shirer
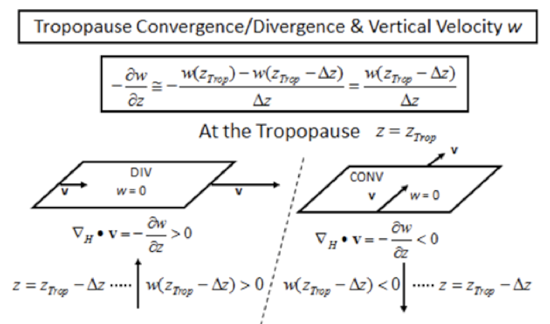
Credit: H.N. Shirer
These processes can be summarized in the following table:
| plane | process | surface area change | ∂w/∂z | w |
| surface | convergence | decrease | + | up |
| surface | divergence | increase | – | down |
| aloft | convergence | decrease | + | down |
| aloft | divergence | increase | – | up |
Let’s now consider the effect that divergence/convergence aloft has on surface convergence/divergence (see figure below).
Divergence aloft is associated with rising air throughout the troposphere, which is associated with low pressure and convergence at the surface.
Convergence aloft is associated with sinking air throughout the troposphere, which is associated with high pressure at the surface and thus divergence at the surface.
So, starting at the surface, the vertical velocity becomes more positive with height when there is surface convergence, reaches some maximum vertical velocity, and then becomes less positive with height again toward the divergence aloft.
Similarly, starting again at the surface, the vertical velocity becomes more negative with height when there is surface divergence, reaches some maximum negative velocity, and then becomes less negative with height again near convergence aloft.
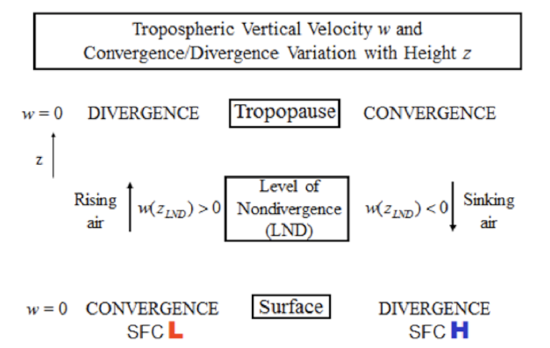
How divergence aloft connects to surface low pressure and convergence and how convergence aloft connects to surface high pressure and divergence.
Credit: H.N. Shirer
Now watch this video (3:52) on horizontal divergence:
Horizontal Divergence Vertical Motion
- Click here for transcript of the Horizontal Divergence Vertical Motion video.
-
The key concepts that allow horizontal divergence to be converted into vertical motion are that mass is conserved, but the air density and density vertical structure are fairly constant with time, and that the vertical wind at Earth's surface and at the tropopause is effectively 0. This means that the total divergence must be approximately 0 so that the air parcel volume remains constant. Thus, changes in the horizontal area cause changes in the vertical height to maintain the air quality. A key to remember is that the vertical velocity w is partial derivative with respect to height z do not always have the same sign. The second key point to remember is that the partial derivative of w with respect to z is a negative divergence. We would look first at diverging mirror surface. But if there is horizontal convergence, then the air must go somewhere, and it cannot go down, so it goes up. The equation actually says that the partial derivative of w, the vertical velocity with respect to z, must be positive. But if w equals 0 at Earth's surface and w is increasingly with altitude, than w must be positive. For divergence near Earth's surface, we see that the partial derivative of w with respect to z is negative, which means that w must be negative above the surface since w equals 0 at earth's surface. So the air velocity w must be downward. But the tropopause, the rapid increase in stress for potential temperature acts like a lid on the troposphere. Effectively makes w go to 0 at the tropopause. There is a horizontal divergence aloft then w must be upward to maintain the air parcel volume as the air parcel spreads out horizontally near the tropopause. Mathematically, this means that w must be positive. But we know that it must go to 0 tropopause. Therefore, the partial of w with respect to z must be negative as it approaches the tropopause, i.e. w is decreasing with increasing height to 0 at the tropopause from a positive value in the troposphere. On the other hand, if there is convergence in the air near the tropopause then, the air must go down and the vertical velocity w must be negative. If we look at the changes in w with respect to height above the level of non-divergence, as z increases, w goes from more negative to less negative, which is a positive change in w, with a positive change in z. So the partial derivative is positive even though w is negative. Putting these pieces together, we see that if we have convergence at Earth's surface, which occurs in low pressure areas for reasons we will see in lesson 10, then at the tropopause, there's divergence. In between the two surfaces the velocity is upward-- that is, w is positive. If we have a divergence near Earth's surface, which occurs in high pressure areas, then there is convergence at the tropopause. In between, the vertical velocity is downward. That is, w is negative. The outward moving air above low pressure creates cooling, which leads to clouds and precipitation. The downward moving air above high pressure region causes warming and drying, resulting in clear conditions.

Credit: Unisys
Credit: NOAA.
We have shown that convergence and divergence aloft near the tropopause is related to surface highs and lows. Now it's your turn to find some examples. Go to a source of information about surface pressure and upper-air winds and pick out some regions that show this relationship. One good source is the Penn State e-Wall, for which you can use the "U.S. Satellite Overlays."


