9.4: How does divergence relate to the air parcel’s area change?
- Page ID
- 3407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We see that divergence is positive when the parcel area grows and is negative when it shrinks. We call growth “divergence” and shrinking “convergence.” We wish to know whether air parcels come together (converge) or spread apart (diverge) or if the parcel area increases with time (divergence) or decreases with time (convergence).
Let’s see how divergence in the horizontal two dimensions is related to area change. We can do a similar analysis that relates divergence in three dimensions to a volume change, but we will stay with the two-dimensional case because it is easier to visualize and also has important applications. Consider a box with dimensions Δx and Δy. Different parts of the box are moving at different velocities (see figure below).
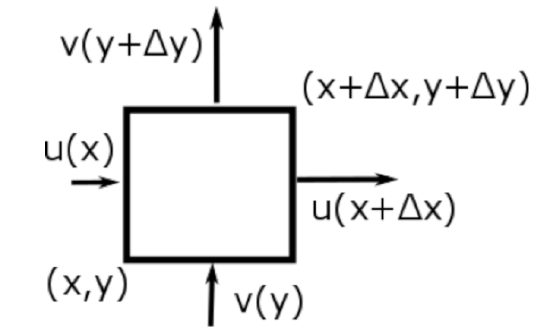
Credit: W. Brune
The box's area, A, is given by:
\(A=\Delta x \Delta y\)
\[\begin{aligned} \frac{d A}{d t}=& \frac{d(\Delta x \Delta y)}{d t}=\Delta x \frac{d(\Delta y)}{d t}+\Delta y \frac{d(\Delta x)}{d t}=\\ & \Delta x[v(y+\Delta y)-v(y)]+\Delta y[u(x+\Delta x)-u(x)] \end{aligned}\]
divide by \(A=\Delta x \Delta y\)
\[\frac{1}{A} \frac{d A}{d t}=\frac{v(y+\Delta y)-v(y)}{\Delta y}+\frac{u(x+\Delta x)-u(x)}{\Delta x}\]
Let \(\Delta y \rightarrow 0, \Delta x \rightarrow 0\)
\[\frac{1}{A} \frac{d A}{d t}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial v}=\vec{\nabla}_{H} \bullet \vec{U}_{H}\]
So we see that the fractional change in the area is equal to the horizontal divergence. Note that the dimension of divergence is time–1 and the SI unit is s–1.
We can do this same analysis for motion in three dimensions to get the equation:
\[\frac{1}{V} \frac{d V}{d t}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\vec{\nabla}_{H} \cdot \vec{U}_{H}+\frac{\partial w}{\partial z}=\vec{\nabla} \cdot \vec{U}\]
where V is the parcel volume. Thus, the 3-D divergence is just the fractional rate of change of an air parcel’s volume.
Exercise
Suppose that an air parcel has an area of 10,000 km2 and it is growing by 1 km2 each second. What is its divergence?
- Click for answer.
-
\(\frac{\Delta A}{\Delta t}=1 \mathrm{km}^{2} \mathrm{s}^{-}\), so
\(\left(\frac{1}{A}\right)\left(\frac{\Delta A}{\Delta t}\right)=\left(\frac{1}{10^{4}} \mathrm{km}^{2}\right)\left(1 \mathrm{km}^{2} \mathrm{s}^{-1}\right)=10^{-4} \mathrm{s}^{-1}\)
Suppose that an air parcel has a area of 10,000 km2 and has a divergence of –10–4 s–1. Is the air parcel growing or shrinking?
- Click for answer.
-
divergence \(=\delta=\left(\frac{1}{A}\right)\left(\frac{\Delta A}{A t}\right),\) or
\(\frac{\Delta A}{A}=\delta \Delta t=\left(-10^{-4} \mathrm{s}^{-1}\right)(1 \mathrm{s})=-10^{-4}\). The air parcel is shrinking.
Check out this video (1:33) for further explanation:
Divergence Area
- Click here for transcript of the Divergence Area video.
-
We can use a very simple demonstration to show how differences in velocity from one end of an air parcel to the other can cause changes in area. Let's let this be our air parcel here, outlined in the dark blue. Several things can happen to this air parcel. One, it can translate. So it can just move with a certain velocity across from left to right. The second thing it can do is it can have a zero velocity here and have a higher velocity here on this end. And it can then grow. And so you see that the area is increasing as time goes on. So we can combine these two motions and see what happens. And so we have some velocity at the parcel, but we have a greater velocity on the right hand side. And we see that as it moves, it grows. It's also possible that as it moves, it shrinks because the velocity on this side is less than the velocity on this side. Then as it moves along, you will see that actually the area's contracting. We can do the same sort of analysis in the y direction. And from this, we can show that in fact, the difference in velocity from here to here can result in the growth or the shrinking of the area of the parcel.
Quiz 9-1: The way the wind blows.
- Find Practice Quiz 9-1 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 9-1. You will be allowed to take this quiz only once. Good luck!


