22.1: Starting with a Big Bang
- Page ID
- 7961
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)According to the big bang theory, the universe blinked violently into existence 13.77 billion years ago (Figure \(\PageIndex{1}\)). The big bang is often described as an explosion, but imagining it as an enormous fireball isn’t accurate. The big bang involved a sudden expansion of matter, energy, and space from a single point. The kind of Hollywood explosion that might come to mind involves expansion of matter and energy within space, but during the big bang, space itself was created.

At the start of the big bang, the universe was too hot and dense to be anything but a sizzle of particles smaller than atoms, but as it expanded, it also cooled. Eventually some of the particles collided and stuck together. Those collisions produced hydrogen and helium, the most common elements in the universe, along with a small amount of lithium.
You may wonder how a universe can be created out of nothing, or how we can know that the big bang happened at all. Creating a universe out of nothing is mostly beyond the scope of this chapter, but there is a way to think about it. The particles that make up the universe have opposites that cancel each other out, similar to the way that we can add the numbers 1 and −1 to get zero (also known as “nothing”). As far as the math goes, having zero is exactly the same as having a 1 and a −1. It is also exactly the same as having a 2 and a −2, a 3 and a −3, two −1s and a 2, and so on. In other words, nothing is really the potential for something if you divide it into its opposite parts. As for how we can know that the big bang happened at all, there are very good reasons to accept that it is indeed how our universe came to be.
Looking back to the early stages of the big bang
The notion of seeing the past is often used metaphorically when we talk about ancient events, but in this case it is meant literally. In our everyday experience, when we watch an event take place, we perceive that we are watching it as it unfolds in real time. In fact, this isn’t true. To see the event, light from that event must travel to our eyes. Light travels very rapidly, but it does not travel instantly. If we were watching a digital clock 1 m away from us change from 11:59 a.m. to 12:00 p.m., we would actually see it turn to 12:00 p.m. three billionths of a second after it happened. This isn’t enough of a delay to cause us to be late for an appointment, but the universe is a very big place, and the “digital clock” in question is often much, much farther away. In fact, the universe is so big that it is convenient to describe distances in terms of light years, or the distance light travels in one year. What this means is that light from distant objects takes so long to get to us that we see those objects as they were at some considerable time in the past. For example, the star Proxima Centauri is 4.24 light years from the sun. If you viewed Proxima Centauri from Earth on January 1, 2015, you would actually see it as it appeared in early October 2010.
We now have tools that are powerful enough to look deep into space and see the arrival of light from early in the universe’s history. Astronomers can detect light from approximately 375,000 years after the big bang is thought to have occurred. Physicists tell us that if the big bang happened, then particles within the universe would still be very close together at this time. They would be so close that light wouldn’t be able to travel far without bumping into another particle and getting scattered in another direction. The effect would be to fill the sky with glowing fog, the “afterglow” from the formation of the universe (Figure \(\PageIndex{1}\)).
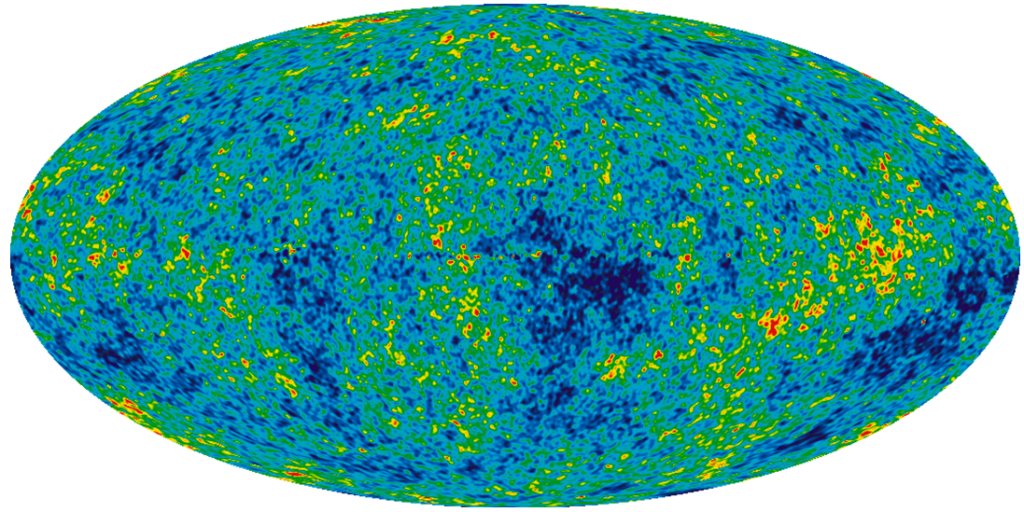
In fact, this is exactly what we see when we look at light from 375,000 years after the big bang. The fog is referred to as the cosmic microwave background (or CMB), and it has been carefully mapped throughout the sky (Figure \(\PageIndex{2}\)). The map displays the cosmic microwave background as temperature variations, but these variations translate to differences in the density of matter in the early universe. The red patches are the highest density regions and the blue patches are the lowest density. Higher density regions represent the eventual beginnings of stars and planets. The map in Figure \(\PageIndex{2}\) has been likened to a baby picture of the universe.
The big bang is still happening, and we can see the universe expanding
The expansion that started with the big bang never stopped. It continues today, and we can see it happening by observing that large clusters of billions of stars, called galaxies, are moving away from us. (The exception is the Andromeda galaxy with which we are on a collision course.) The astronomer Edwin Hubble came to this conclusion when he observed that the light from other galaxies was red-shifted. The red shift is a consequence of the Doppler effect. This refers to how we see waves when the object that is creating the waves is moving toward us or away from us.

Before we get to the Doppler effect as it pertains to the red shift, let’s see how it works on something more tangible. The duckling swimming in Figure \(\PageIndex{3}\) is generating waves as it moves through the water. It is generating waves that move forward as well as back, but notice that the ripples ahead of the duckling are closer to each other than the ripples behind the duckling. The distance from one ripple to the next is called the wavelength. The wavelength is shorter in the direction that the duckling is moving, and longer as the duckling moves away.
When waves are in air as sound waves rather than in water as ripples, the different wavelengths manifest as sounds with different pitches—the short wavelengths have a higher pitch, and the long wavelengths have a lower pitch. This is why the pitch of a car’s engine changes as the car races past you.
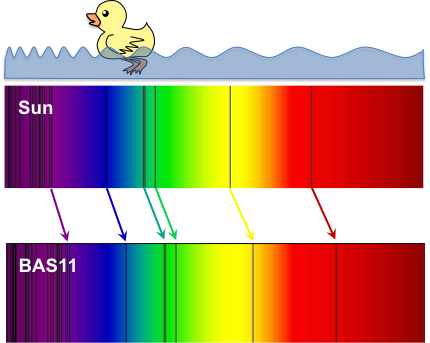
For light waves, wavelength translates to color (Figure \(\PageIndex{4}\)). In the spectrum of light that we can see, shorter wavelengths are on the blue end of the spectrum, and longer wavelengths are on the red end of the spectrum. Does this mean that galaxies look red because they are moving away from us? No, but the color we see is shifted toward the red end of the spectrum and longer wavelengths.
Notice that the sun’s spectrum in the upper part of Figure \(\PageIndex{4}\) has some black lines in it. The black lines are there because some colors are missing in the light we get from the Sun. Different elements absorb light of specific wavelengths, and many of the black lines in Figure \(\PageIndex{4}\) represent colors that are absorbed by hydrogen and helium within the Sun. This means the black lines are like a bar code that can tell us what a star is made of. The lower spectrum in Figure \(\PageIndex{4}\) is the light coming from BAS11, an enormous cluster of approximately 10,000 galaxies located 1 billion light years away. The black lines represent the same elements as in the Sun’s spectrum, but they are shifted to the right toward the red end of the spectrum because BAS11 is moving away from us as the universe continues to expand. So to summarize, because almost all of the galaxies we can see have light that is red-shifted, it means they are all moving away from us. In fact, the farther away they are, the faster they are going. This is evidence that the universe is still expanding.
Media Attributions
- Figure \(\PageIndex{1}\): “Time Line of the Universe” by NASA and WMAP Science Team. Adapted by Karla Panchuk. Public domain.
- Figure \(\PageIndex{2}\): “Nine Year Microwave Sky” by NASA/ WMAP Science Team. Public domain.
- Figure \(\PageIndex{3}\): “Duck and Ducklings” by M. Harkin. Adapted by Karla Panchuk. CC BY.
- Figure \(\PageIndex{4}\): “Spectra” by Harold Stokes. Adapted by Karla Panchuk. Public domain.


