8.5: Other Dating Methods

There are numerous other techniques for dating geological materials, but we will examine just two of them here: tree-ring dating (i.e., dendrochronology) and dating based on the record of reversals of Earth’s magnetic field.

Dendrochronology can be applied to dating very young geological materials based on reference records of tree-ring growth going back many millennia. The longest such records can take us back to 25 ka, to the height of the last glaciation. One of the advantages of dendrochronology is that, providing reliable reference records are available, the technique can be used to date events to the nearest year.

Dendrochronology has been used to date the last major subduction-zone earthquake on the coast of B.C., Washington, and Oregon. When large earthquakes strike in this setting, there is a tendency for some coastal areas to subside by one or two meters. Seawater then rushes in, flooding coastal flats and killing trees and other vegetation within a few months. There are at least four locations along the coast of Washington that have such dead trees (and probably many more in other areas). Wood samples from these trees have been studied and the ring patterns have been compared with patterns from old living trees in the region (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\) Example of tree-ring dating of dead trees.

Figure \(\PageIndex{2}\) Sites in Washington where dead trees are present in coastal flats. The outermost wood of eight trees was dated using dendrochronology, and of these, seven died during the year 1699, suggesting that the land near to the coast was inundated by water at that time.

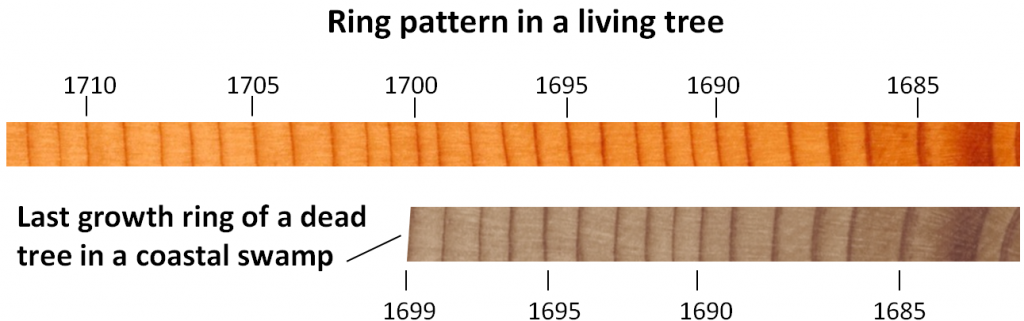
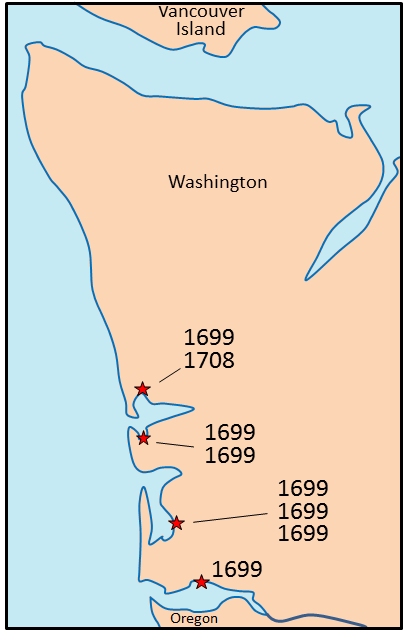
At all of the locations studied, the trees were found to have died either in the year 1699, or very shortly thereafter (Figure \(\PageIndex{2}\)). On the basis of these results, it was concluded that a major earthquake took place in this region sometime between the end of growing season in 1699 and the beginning of the growing season in 1700. Evidence from a major tsunami that struck Japan on January 27, 1700, narrowed the timing of the earthquake to sometime in the evening of January 26, 1700. For more information, see The 1700 Juan de Fuca Earthquake.

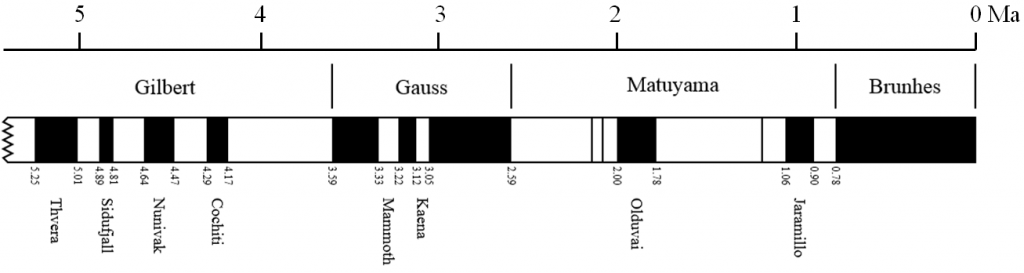
Changes in Earth’s magnetic field can also be used to date events in geologic history. The magnetic field makes compasses point toward the North Pole, but, as we’ll see in Chapter 10, this hasn’t always been the case. At various times in the past, Earth’s magnetic field has reversed itself completely, and during those times a compass would have pointed to the South Pole. By studying magnetism in volcanic rocks that have been dated isotopically, geologists have been able to delineate the chronology of magnetic field reversals going back to 250 Ma. About 5 million years of this record is shown in Figure \(\PageIndex{3}\), where the black bands represent periods of normal magnetism (“normal” meaning similar to the current magnetic field) and the white bands represent periods of reversed magnetism. These periods of consistent magnetic polarity are given names to make them easier to reference. The current normal magnetic field, known as Brunhes, has lasted for the past 780,000 years. Prior to that there was a short reversed period and then a short normal period known as Jaramillo.

Figure \(\PageIndex{3}\) The last 5 Ma of magnetic field reversals.

Oceanic crust becomes magnetized by the magnetic field that exists as the crust forms from magma. As it cools, tiny crystals of magnetite that form within the magma become aligned with the existing magnetic field and then remain that way after all of the rock has hardened, as shown in Figure \(\PageIndex{4}\). Crust that is forming today is being magnetized in a “normal” sense, but crust that formed 780,000 to 900,000 years ago, in the interval between the Brunhes and Jaramillo normal periods, was magnetized in the “reversed” sense.

Chapter 9 has a discussion of Earth’s magnetic field, including where and how it is generated and why its polarity changes periodically.

Figure \(\PageIndex{4}\) Depiction of the formation of magnetized oceanic crust at a spreading ridge. Coloured bars represent periods of normal magnetism, and the small capital letters denote the Brunhes, Jaramillio, Olduvai, and Gauss normal magnetic periods (see Figure \(\PageIndex{2}\)).

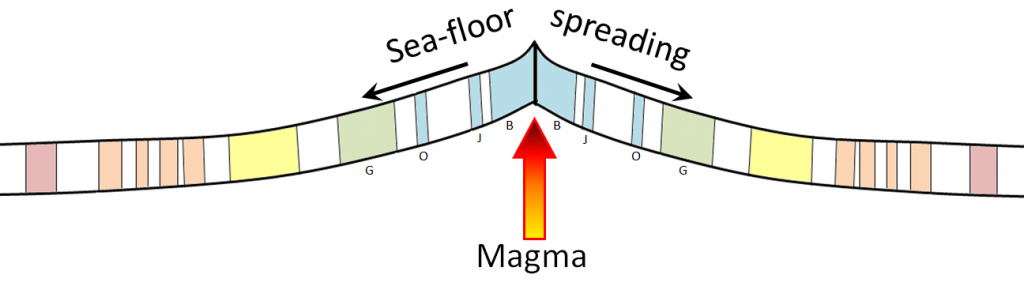
Magnetic chronology can be used as a dating technique because we can measure the magnetic field of rocks using a magnetometer in a lab, or of entire regions by towing a magnetometer behind a ship or an airplane. For example, the Juan de Fuca Plate, which lies off of the west coast of B.C., Washington, and Oregon, is being and has been formed along the Juan de Fuca spreading ridge (Figure \(\PageIndex{5}\)). The parts of the plate that are still close to the ridge have normal magnetism, while parts that are farther away (and formed much earlier) have either normal or reversed magnetism, depending on when the rock formed. By carefully matching the sea-floor magnetic stripes with the known magnetic chronology, we can determine the age at any point on the plate. We can see, for example, that the oldest part of the Juan de Fuca Plate that has not subducted (off the coast of Oregon) is just over 8 million years old, while the part that is subducting underneath Vancouver Island is between 0 and about 6 million years old.

Figure \(\PageIndex{5}\) The pattern of magnetism within the area of the Juan de Fuca Plate, off the west coast of North America. The colored shapes represent parts of the sea floor that have normal magnetism, and the magnetic time scale is shown using the same colors. The blue bands represent Brunhes, Jaramillo, and Olduvai; the green represents Gauss; and so on. (Note that in this diagram, sea-floor magnetism is only shown for the Juan de Fuca Plate, although similar patterns exist on the Pacific Plate.)

Exercise 8.4 Magnetic dating

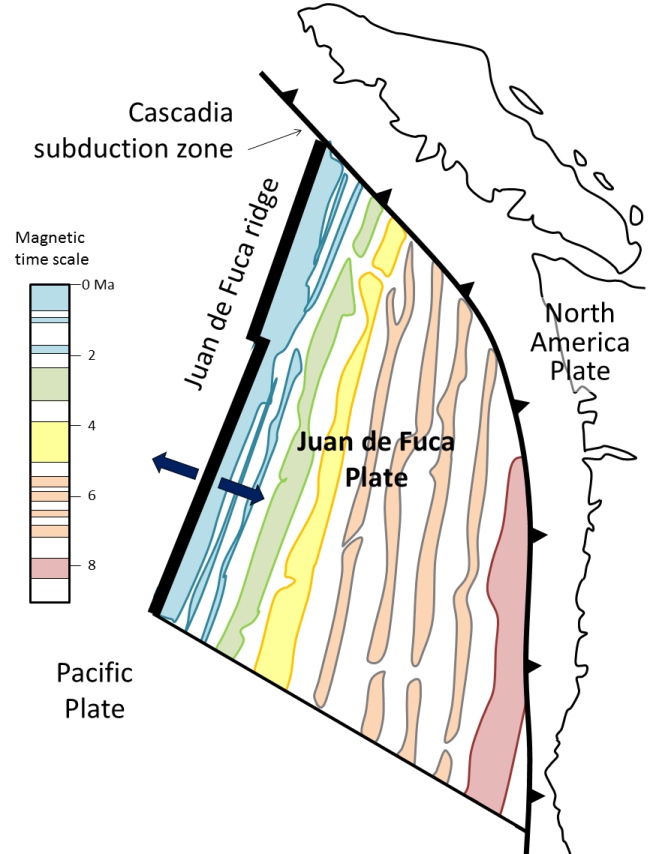
The fact that magnetic intervals can only be either normal or reversed places significant limits on the applicability of magnetic dating. If we find a rock with normal magnetism, we can’t know which normal magnetic interval it represents, unless we have some other information.

Using Figure \(\PageIndex{3}\) for reference, determine the age of a rock with normal magnetism that has been found to be between 1.5 and 2.0 Ma based on fossil evidence.

How about a rock that is limited to 2.6 to 3.2 Ma by fossils and has reversed magnetism?

See Appendix 3 for Exercise 8.4 answers.

Media Attributions

• Figures 8.5.1, 8.5.4, 8.5.5: © Steven Earle. CC BY.
• Figure \(\PageIndex{2}\): © Steven Earle. CC BY. From data in Yamaguchi, D.K., B.F. Atwater, D.E. Bunker, B.E. Benson, and M.S. Reid. 1997. Tree-ring dating the 1700 Cascadia earthquake. Nature, Vol. 389, pp. 922 – 923, 30 October 1997.
• Figure \(\PageIndex{3}\): “Geomagnetic polarity late Cenozoic” by the USGS. Adapted by Steven Earle. Public domain.