13.7.2: Sheet Silicates

Figure 13.30: The atomic arrangements in three sheet silicates

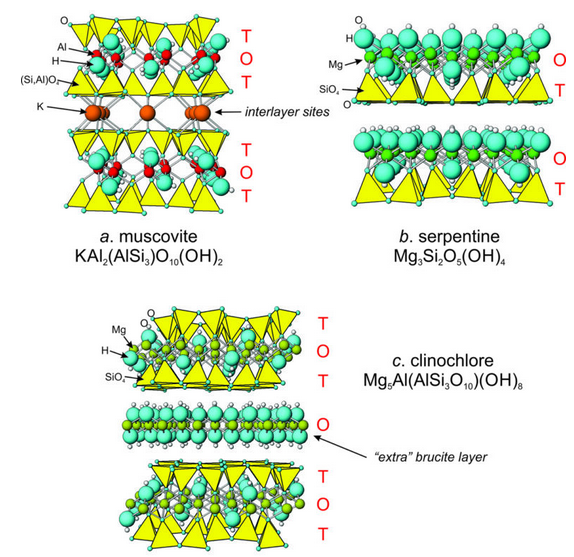
Sheet silicates are planar structures containing several different kinds of layers. One consequence is that sheet silicates can accommodate cations of all sizes. Tetrahedral layers (labeled T in Figure 13.30) consist mostly of SiO₄ tetrahedra, sometimes with lesser amounts of AlO₄ tetrahedra. Octahedral layers (O) contain divalent and trivalent cations (e.g., Fe²⁺, Mg²⁺, Al³⁺) in 6-fold coordination.

We call the octahedral layers gibbsite layers if they contain Al³⁺ and brucite layers if they contain Mg²⁺ or Fe²⁺ – because the structures of the layers resemble the structures of the minerals gibbsite and brucite. Besides tetrahedral and octahedral layers, micas have interlayer sites containing alkalis or alkali earth cations, most commonly K⁺, Na⁺, Li⁺, or Ca²⁺.

Figure 13.30a shows the atomic arrangement in muscovite, the most common of the sheet silicates. The structure of muscovite, and of all the other micas, consists of sequences of TOT-alkali-TOT-alkali, repeating many times. The thickness of one repeat sequence is about 10 Å.

Some sheet silicates, like muscovite, are dioctahedral, meaning they contain two Al³⁺ cations for every four (Si,Al) tetrahedra. Other sheet silicates, including biotite, K(Mg,Fe)₃(AlSi₃O₁₀)(OH)_2, contain three divalent cations for every four tetrahedra. They are trioctahedral. Thus, the arrangement of atoms in biotite is identical to that in muscovite, except that three Mg²⁺ or Fe²⁺ replace every two Al³⁺ cations in the octahedral sites. In both muscovite and biotite, one of every four tetrahedra contains Al³⁺ instead of Si⁴⁺. An interlayer K⁺ provides the missing charge. Pyrophyllite, Al₂Si₄O₁₀(OH)_2, and talc, Mg₃Si₄O₁₀(OH)₂, have structures identical to muscovite and biotite except that the K⁺ layer is absent. Consequently, all tetrahedra are SiO₄.

Tetrahedral (T) and octahedral (O) layers may stack in various ways. In the micas, pyrophyllite, and talc, tetrahedral layers are above and below octahedral layers, producing TOT sandwiches. In serpentine, Mg₃Si₂O₅(OH)₄, and kaolinite Al₂Si₂O₅(OH)₄, T- and O-layers alternate. The arrangement is a little like open-face sandwiches with TO sandwiches piled on top of each other. For example, Figure 13.30b shows the atomic arrangement in serpentine, a trioctahedral sheet silicate. Layers of SiO₄ tetrahedra alternate with layers of Mg octahedra in brucite layers. Kaolinite (dioctahedral) has a similar structure except that two Al³⁺ (gibbsite layers) replace every three Mg²⁺ (brucite layers). The layers in serpentine and kaolinite repeat about every 7 Å.

Figure 13.30c shows the atomic arrangement of clinochlore, one of the more common chlorite minerals. Figure 6.69 (Chapter 6) showed a photo of clinochlore. Unlike micas, in chlorites, additional brucite layers (octahedral) separate the TOT sandwiches. And in other sheet silicates the stacking may be even more complex. Clay minerals, in particular, have complicated multilayered structures involving interlayers of H₂O. The repeat distance for layers in clinochlore is about 14 Å; in clay minerals may it be 16 Å or greater.

Individual tetrahedral or octahedral layers in sheet silicates have 3-fold or 6-fold symmetry. So, if the different layers piled up aligned, crystals would be trigonal or hexagonal. However, the layers are sightly offset and 3-fold and 6-fold symmetry does not persist in 3D. Most sheet silicates are monoclinic or triclinic. Micas (and other sheet silicates) have several different polymorphs, related by the way in which TOT and TO sheets stack with respect to each other. The minerals also commonly twin, but the subtle distinctions between polymorphs and the twinning are difficult to detect without detailed X-ray or transmission electron microscope studies.

The photos below show muscovite, antigorite (a variety of serpentine), and margarite (a Ca-bearing mica). Photos of several other varieties of micas are in Chapters 6:Figure 6.61, Figure 6.62, Figure 6.63, Figure 6.64, Figure 6.65, and Figure 6.66. Other photos of serpentine can be seen in Figures 8.72, 8.73, and 8.74 (Chapter 8).

Figure 13.31: Muscovite from Minas Gerais, Brazil. The specimen is 11 cm tall.

Figure 13.32: Antigorite (serpentine) from the Shetland Islands. The specimen is 11 cm wide.

Figure 13.33: Silver-pink margarite from Chester, Massachusetts