13.4.2: Pauling’s Second Rule

Figure 13.17: Atoms in sylvite

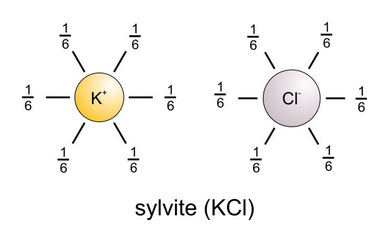
Pauling’s second rule, sometimes called the Electrostatic Valency Principle, says that we can calculate the strength of a bond (its electrostatic valence) by dividing an ion’s valence by its C.N. Consequently, the sum of all bonds to an ion must be equal to the charge on the ion. In sylvite (KCl), six Cl^– bond to each K⁺ and the strength of each bond is 1/6, total charge divided by number of bonds (Figure 13.17). The strength of each bond around Cl^– is 1/6 as well. Six bonds of charge 1/6 add up to 1, the charge on each ion.

Figure 13.18: The atomic arrangement in rutile

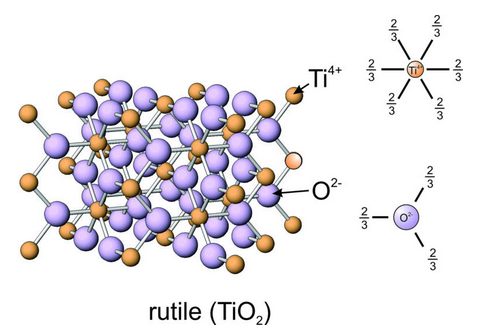
We can use Pauling’s first two rules to analyze a more complicated mineral, rutile (TiO₂). In rutile, Ti-O bonds are the only bonds present (Figure 13.18). The radii of Ti⁴⁺ and O^2– are 0.69 Å and 1.32 Å. R_c/R_a is 0.52 and, as predicted by Rule 1, Ti⁴⁺ is in 6-fold (octahedral) coordination – shown in the enlarged coordination drawing in this figure. Each bond has a strength of 4/6 (total charge divided by number of bonds) = 2/3. Since each O^2– has a total charge of -2, it must be bonded to three Ti⁴⁺ to satisfy Rule 2, so O^2- is in triangular coordination (Figure 13.18).

Although Pauling’s first two rules are useful guides to crystal structures, they have shortcomings. First, ionic radii vary with C.N. and valence, among other things. Sometimes radius-ratio calculations may be ambiguous because they require choosing a C.N. before we may make calculations (see Box 13-3). Second, bonds in minerals are rarely completely ionic, and ionic radius varies with the nature of the bond. Third, in cases where R_c/R_a is near a limiting value, we cannot be certain whether the higher or lower C.N. will prevail. Fourth, some coordination polyhedra, especially for high C.N.s, may be irregular in shape.

13.4.2.1 Isodesmic, Anisodesmic, and Mesodesmic Crystals

Figure 13.19: Bond strengths in spinel

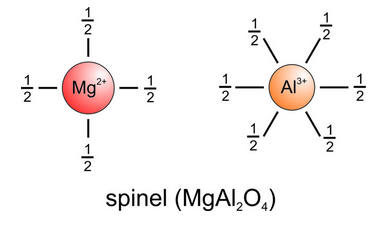
Halite, sylvite, fluorite, and rutile are relatively simple minerals; they each contain one cation and one anion and, therefore, one kind of bond. Most minerals contain more than two elements and may have many kinds of bonds. We saw a model of spinel, MgAl₂O₄, in Figure 13.10. Spinel contains Mg-O and Al-O bonds. X-ray studies reveal that Mg²⁺ is in tetrahedral coordination and Al³⁺ is in octahedral coordination. Consequently, as shown in Figure 13.19,the strength of the bonds around Mg²⁺ is 2/4 = 1/2, and the strength of the bonds around Al³⁺ is 3/6 = 1/2. We call compounds such as spinel, in which all bonds have the same strength, isodesmic. They have the same bond lengths and properties (e.g., cleavage and hardness) in all directions.

Figure 13.20: Bonds around S⁶⁺ in anhydrite

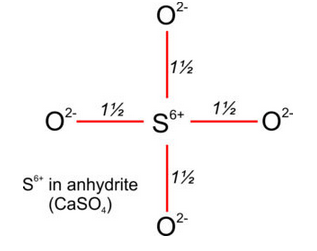
Figure 13.2 showed the atomic arrangement in anhydrite, CaSO₄. Anhydrite and other sulfates are examples of anisodesmic compounds. In sulfates, S⁶⁺ is in 4-fold coordination with O^2–. The strength of a sulfur-oxygen (S-O) bond (shown in red in Figure 13.20) is therefore 6/4 = 1½ (Figure 13.20). Because the strength of each S-O bond is greater than half the charge on coordinating oxygen, oxygen bonds to S⁶⁺ more tightly than to Ca²⁺. Consequently, (SO₄)^2– molecules are tight units within the crystal structure. All sulfates, carbonates, nitrates, and other anisodesmic compounds contain tightly bonded molecular ions. So, we can think of (SO₄)^2–, (CO₃)^2–, and (NO₃)^– as single anionic units within crystals.

Figure 13.21: Mesodesmic bonds joining silicon and oxygen ions

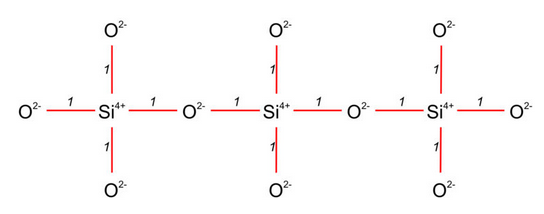
Silicate minerals belong to a special group of compounds that are mesodesmic. If a bond distribution is mesodesmic, cation-anion bond strength equals exactly half the charge on the anions. In silicates, Si⁴⁺ is in tetrahedral coordination and each Si-O bond (shown red in Figure 13.21) has a strength of 1, exactly half the charge of O^2–. Consequently, oxygen may coordinate to another cation just as strongly as to its coordinating Si⁴⁺. In many silicates, some of the “other” cations are another Si⁴⁺. For example in Figure 13.21, pairs of Si⁴⁺ share an oxygen producing chains of Si⁴⁺ alternating with O^2-. Mesodesmic bonding is why silica tetrahedra can polymerize to form pairs, chains, sheets, or networks. It also helps explain why many silicate minerals are quite hard; the Si-O bonds are very strong.