13.4.3: Pauling’s Third Rule

Last updated
Save as PDF

Page ID: 18353

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

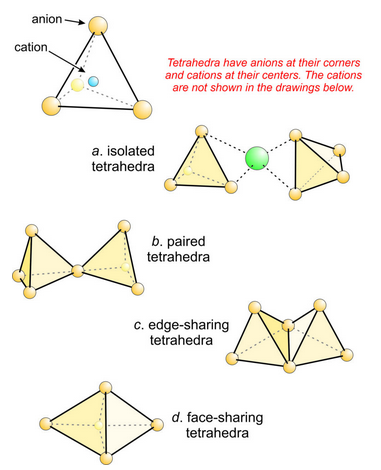
13.22.jpg — Figure 13.22: Silicon tetrahedra and sharing of anions

In all crystals, anions bond to more than one cation. For example, Figure 13.22 shows several ways silica tetrahedra might be associated in an atomic structure. In Figure 13.22a, tetrahedra do not share any common oxygen. They are isolated tetrahedra linked by bonds to a cation between them. In 13.22b, a pair of tetrahedra share one oxygen (called a bridging oxygen). Bonding of these two sorts commonly holds crystal structures together.

In Figure 13.22c, adjacent tetrahedra share an edge (two oxygen). In Figure 13.22d, they share a face (three oxygen). We can see that as the structure progresses from Figure 13.22a to 13.22d, Si⁴⁺ in the centers of the tetrahedra get closer together. Yet, because the Si⁴⁺ are all positively charged, we expect them to repel each other. This is the essence of Pauling’s third rule. The third rule is that coordinating polyhedra become less stable when they share edges and are extremely unstable if they share faces. Instability results because if polyhedra share edges or faces, cations in the centers of the polyhedra are too close together. The instability is especially important for cations of high charge, high C.N., or in cases when R_c/R_a is near limiting values.

Although this discussion of Pauling’s third rule is focused on tetrahedra, the same principles apply to octahedra and other polyhedra. Edge- and even sometimes face-sharing, however is more common in larger polyhedra than in tetrahedra because there is more room for cations to stay apart.