13.4.1: Pauling’s First Rule
- Page ID
- 18351
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Pauling’s first rule, sometimes called the Radius Ratio Principle, states that the distance between cations and anions can be calculated from their effective ionic radii, and that cation coordination number depends on the relative ratio of cation and surrounding anion radii. In essence, this rule says that very small cations will bond to only a few anions, while very large cations may bond to many anions. In other words, as the radius of the cation increases, so too will the coordination number.
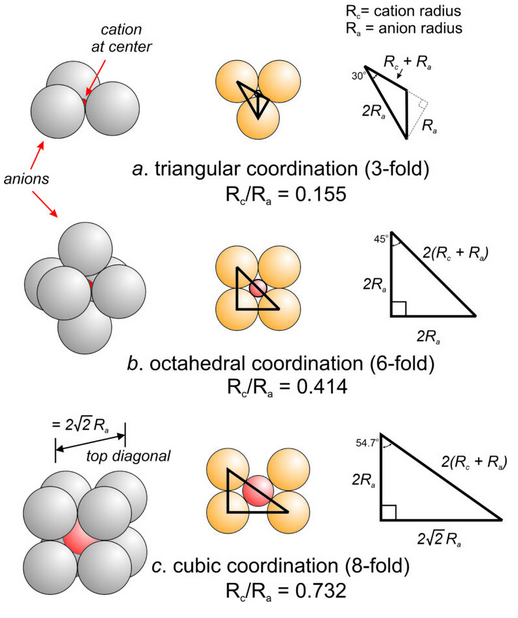
Figure 13.15a shows the limiting case when a cation just fits into the opening between three touching anions. Application of the Pythagorean theorem, which is a bit complicated, reveals that the ratio of cation radius to anion radius (Rc/Ra) = 0.155.
Figure 13.15b shows four touching anions with a cation between. If additional anions are directly above and below the cation, the cation is in perfect octahedral coordination. Application of the Pythagorean theorem to the right triangle reveals the ratio of cation radius to anion radius (Rc/Ra) to be 0.414. This value is the square root of 2 minus 1.
Figure 13.15c shows similar calculations for a cation in cubic coordination. (Rc/Ra) comes out to be 0.732. This value is the square root of 3 minus 1. We can make similar, though more complicated, calculations for cations in other coordinations. It should not be surprising, however, that the (Rc/Ra) value for perfect dodecahedral coordination is the square root of 4 minus 1 = 1. The pattern involving square roots is because the calculations all involve the Pythagorean theorem.
As coordination number increases, space between anions increases, and the size of the cation that fits increases. Pauling argued, therefore, that as Rc/Ra increases, cations will move from 2- or 3-fold to higher coordinations in atomic structures. He further argued that stretching a polyhedron to hold a cation larger than ideal might be possible. However, it was unlikely, he said, that a polyhedron would be stable if cations were smaller than ideal. In nature, the upper limits given for various coordinations are sometimes stretched; the lower ones are rarely violated. The table below summarizes the different limiting ratios for different coordinations.
| Rc/Ra | expected coordination | coordination number |
|---|---|---|
| <0.15 | 2-fold coordination | 2 |
| 0.15 0.15– 0.22 |
perfect triangular coordination triangular coordination |
3 |
| 0.22 0.22– 0.41 |
perfect tetrahedral coordination tetrahedral coordination |
4 |
| 0.41 0.41– 0.73 |
perfect octahedral coordination octahedral coordination |
6 |
| 0.73 0.73– 1.0 |
perfect cubic coordination cubic coordination |
8 |
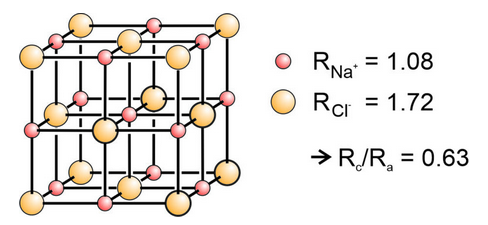
As an example of application of Pauling’s first rule, let’s take another look at halite. The radii of Na+ and Cl– in octahedral coordination are 1.08Å and 1.72Å. The radius ratio, Rc/Ra, is 1.08/1.72 = 0.63. Thus we can expect the cation Na+ to be in octahedral (6-fold) coordination, consistent with the model shown here in Figure 13.16 (and in Figure 13.5a). If Na+ is in 6-fold coordination, Cl– must be as well, since the structure contains an equal number of both.
For a video discussing coordination polyhedra and the coordinations of cations in olivine (an example of application of Pauling’s Rule #1), click on the link below:
blankVideo 13-2: https://www.youtube.com/watch?v=hUmTK0hI5EA (8 minutes)


