13.2.2: Coordination Number

Most minerals, except native elements such as gold or copper, contain anions or anionic molecules. O^2-, S^2-, (OH)^–, and (CO₃)^2- are especially common. The large size of oxygen and other anions (and molecules) compared with most common cations (Figure 13.7) means that we can often think of crystal structures as large anions with small cations in interstices (spaces) between them. Anions are packed in a repetitive structure, with the cations at regular intervals throughout. The number of anions to which some particular cation bonds is the cation’s coordination number (C.N.). Si⁴⁺, for example, nearly always bonds to four O^2- anions in minerals, and therefore has a C.N. of 4. So we say it is “in 4-fold coordination.”

The size of interstices between anions depends on how the anions are packed. In two dimensions, anions can fit together in symmetrical patterns to form hexagonal or square patterns. In three dimensions, other possibilities, including tetrahedral and cubic arrangements, exist.

Figure 13.9: Different kinds of coordination

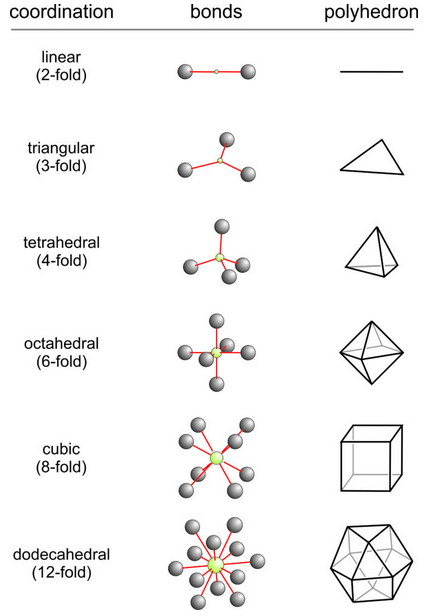
Figure 13.4 showed one way a group of identical anions may pack around a single cation. The cation was in 4-fold coordination, but there are other possibilities, shown here in Figure 13.9. In this figure, because only one cation and one kind of anion are involved, all bond distances (in red) are the same. We give coordination arrangements geometrical names depending on the shape of the polyhedron created by connecting the centers of the anions.

We call 2-fold coordination linear because the ions form a line. We call 3-fold coordination triangular because the anions form a triangle. We call 4-fold coordination tetrahedral because the four anions form a tetrahedron. We call the 6-fold coordination octahedral because the anions outline an octahedron (an eight-sided geometric shape). We call the 8-fold coordination cubic because connecting the centers of the anions produces a cube. (Fortunately, we never call cubic coordination hexahedral although a cube has six faces.) We call the 12-fold coordination, shown in Figure 13.9, dodecahedral because the coordinating polyhedron has twelve vertices.

As coordination number increases, the space inside a polyhedron increases to accommodate larger cations. So, large cations have greater C.N.s than small cations. The coordination polyhedra shown in Figure 13.9 are all regular, meaning the cation-to-anion distance is the same for all anions. Cations also sometimes occupy distorted sites or sites with irregular or unusual coordinations not represented by the drawings in Figure 13.9. Most of the time, regular geometry is present.

Common elements have different coordinations in different minerals. Most atoms in minerals are in 3-, 4-, 6-, or 8-fold coordination, but 5-fold, 7-fold, 9-fold, and 10-fold coordinations are possible. 2-fold coordination is rare or nonexistent. The atoms in some native metals are in 12-fold coordination.

Figure 13.10: The atomic arrangement in spinel

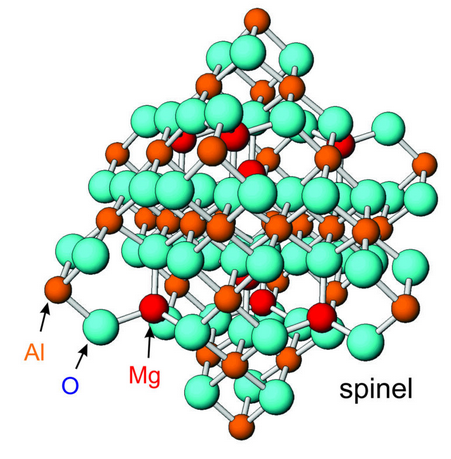
Figure 13.10 shows a typical ball-and-stick model for spinel, MgAl₂O₄. This model is convenient and easy to examine, and we can count the number of bonds to each atom. But the depiction is incorrect in detail because balls of nearly the same size, separated by large distances, represent all atoms, anions, or cations, and there is lots of unoccupied space. More accurate models of crystal structures could better reflect variations in ionic radii, bond length, and the way that ions fit together. In principle we could construct very exact models, using spheres of correctly proportioned sizes. In practice it is not often done because regular ball-and-stick models are easier to make and examine, and because we know that the notion of ions as spheres is only an approximation.