13.2.1: Ionic Radii

Last updated
Save as PDF

Page ID: 18344

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ions consist of nuclei with electron clouds around them. The electrons are constantly moving; sometimes they are farther from the nucleus than at other times, so we can never know the exact size of the electron cloud. However, ions often behave as if they have fixed radii, and we can understand many crystal properties by thinking of crystals as collections of spherical ions packed together. The spacing between them, and the way they pack together, are functions of their size. Knowing their effective ionic radius is therefore useful. Figure 13.7 compares average effective ionic radii for common anions and cations.

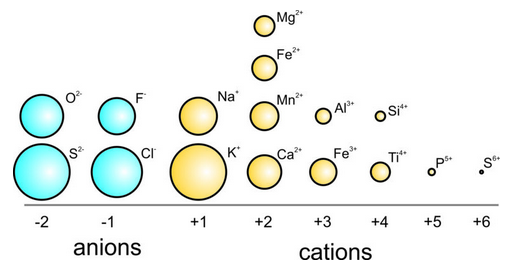
13.7.jpg — Figure 13.7: Comparing the sizes of common cations and anions

How can we determine ionic radii if ions really do not have a fixed radius? We estimate size by studying bond lengths in crystals. Consider the mineral periclase (MgO) shown in Figure 13.6. Through X-ray diffraction studies we have learned that the distance between the centers of the Mg²⁺ and O^2- ions is about 2.11 Å, so the sum of the effective ionic radii of Mg²⁺ and O^2- is 2.11 Å. A standard value for the radius of O^2- is 1.32 Å, so this yields a radius of 0.79 Å for Mg²⁺ in periclase. Crystallographers have also measured the radius of an Mg atom by using X-ray to learn the distance between neighboring Mg atoms in Mg metal. Mg metal is not, however, ionically bonded, and the results do not tell us the radius of Mg²⁺, although they do tell us that metallic Mg has a radius of about 1.60 Å.

If we study many compounds, it becomes possible to learn the effective ionic radii of all individual elements in their most common ionic forms. Consider the alkali oxides. They have the general formula R₂O, and R can be any alkali element. Oxygen bonds to each alkali ion, and chemists and mineralogists have determined the bond lengths through X-ray studies. Since the radius of O^2- is common to all alkali oxides, variations in bond length must be due to variations in the radii of the alkalis. If we assume O^2- has a constant radius of 1.32 Å, we get the cation radii in the table below. The alkalis are in column 1 (Group 1) of the Periodic Table. It should be no surprise that alkali radius increases as we move down the column because we know elements with higher atomic numbers have more protons and electrons, and so are larger atoms.

Radii of Alkali Cations in Alkali Oxides
cation	Li⁺	Na⁺	K⁺	Rb⁺	Cs⁺
at. no.	3	11	19	37	55
radius Å	0.82	1.40	1.68	1.81	1.96

The table above shows radii of alkali cations increasing with atomic number (down a row in the Periodic Table). Radii also vary systematically across a row of the Periodic Table (see the table below). Cation radii are always smaller than uncharged atoms of the same species. As we move from the left margin of the Periodic Table toward the center, cation charge increases and cations get smaller because more charge means attraction between electrons and protons increases.

Radii of Common Ions in the Third Period (Row) of the Periodic Table
cation	Na⁺	Mg²⁺	Al³⁺	Si⁴⁺	P⁵⁺	S⁶⁺	S^2-	Cl^–	Ar⁰
at. no.	11	12	13	14	15	16	16	17	18
radius Å	1.18	0.79	0.55	0.41	0.25	0.20	1.72	1.70	—

The table above also includes two anions (S^2- and Cl^–) from the right-hand side of the Periodic Table; they are larger than the cations because they contain extra electrons in outer orbitals. Anion radii are always larger than uncharged atoms of the same species. Note that we cannot list an ionic radius for argon because it is a noble gas and does not ionize to enter ionic structures.

We can best see the relationship between cation radius and charge by looking at elements that exist in more than one valence state. For example, the tables below give ionic radii for manganese and vanadium cations. As expected, the radii decrease with charge, reflecting the greater pull nucleus protons have on outer electrons with increasing charge.

Radii of Manganese Atoms and Cations
cation	Mn⁰	Mn²⁺	Mn³⁺	Mn⁴⁺	Mn⁶⁺	Mn⁷⁺
radius Å	1.12	0.97	0.70	0.62	0.35	0.34

Radii of Vanadium Atoms and Cations
cation	Va⁰	Va²⁺	Va³⁺	Va⁴⁺	Va⁵⁺
radius Å	1.31	0.87	0.72	0.67	0.53

Box 13-2 contains a table with effective ionic radii for the most common ions. The table includes more than one value for most ions because radius varies depending on how an ion is bonded. For example, the radius of Na⁺ is listed as 1.07, 1.08, and 1.40 Å; these difference reflect different numbers of bonds going to the cation. And the radii of Na⁺ given in some tables above are inconsistent because one table refers to alkali oxides, and the other contains average values for many different types of crystals. These differences remind us that the notion of ionic radius is an approximation because the effective radius of an ion depends on several things:

Most significantly, radii are only constant if bond types are constant. For example, the average ionic radius of Mg²⁺ is 0.88 Å, while its covalent radius is 1.36 Å and its metallic radius is 1.60 Å.
Additionally, ionic size varies depending on the number of bonds (called the coordination number, discussed below) that connect to an ion.
Another complication may arise because in some structures ions become polarized (elongated) in one direction and no longer act as spheres.
A final ambiguity arises because we assume a value for the radius of O^2- to calculate radii for cations bonded to oxygen. Depending on the kind of bonding and several other things, O^2- may have an effective radius between 1.27 Å and 1.34 Å, but the values in this book’s tables are based on an assumed radius of 1.32 Å.

Coordination Numbers and Effective Ionic Radii

13.8.png — Figure 13.8: Effective ionic radii for ions in different coordinations

The chart seen here (click to enlarge) gives effective ionic radii for the most common ions. These data are slightly modified from values in Zoltai and Stout (1984) Mineralogy: Concepts and Principles. The literature contains many different tables with values that do not match those given here because radii are approximations and may be determined in different ways. For consistency, values from different sources should not be combined.

Most of the elements listed in Figure 13.8 have several different values of ionic radius listed. The first number in every entry is the coordination number. The second number (for cations) is the effective ionic radius in coordination with O^2- having a radius of 1.32 Å. Values for elements in parentheses were not determined.

Video 13-1: Further discussion about why ionic radii can vary, even for the same element