12.1.15: Data and Processing

Last updated
Save as PDF

Page ID: 18380

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

When we X-ray a powdered sample, we obtain a powder diffraction pattern. The key information from the pattern is a list of d-values with diffraction intensities. Each d-value corresponds to sets of planes, and the intensity is a measure of how many atoms are on those planes. Because different minerals have different atomic arrangements, they yield different patterns.

Computers controlling powder diffractometers collect and process data automatically. They compare diffraction results with data bases to identify the mineral or minerals present. The most comprehensive reference, the X-ray Powder Diffraction File (PDF) compiled by the International Centre for Diffraction Data, is available in computerized databases and contains information on almost 6,000 minerals and tens of thousands of other inorganic and organic crystalline compounds.

Simple mineral identification may require only a few minutes. For extremely precise results, however, data collection may take hours or longer. However, a shortcoming of computer interpretations is that they are “black box” procedures; they do not improve our knowledge or understanding of powder diffractometry and may occasionally produce misidentifications. And, for mixes of more than one mineral, computer programs always give an analysis but it is sometime difficult to evaluate the accuracy of the results.

To visualize diffraction measurements, we typically look at a diffraction pattern like the one below in Figure 12.24. It shows a diffraction pattern, also called a powder pattern, or a diffractogram, for halite. In standard diffraction patterns like this one, the X-axis is 2θ in degrees and the Y-axis is the intensity of diffraction. Following Bragg’s Law, d-value is infinite at 0^o 2θ but decreases quickly with increasing angle. It is less than 20 Å at 5^o 2θ, and then falls slowly to about 1 Å at 90^o 2θ.

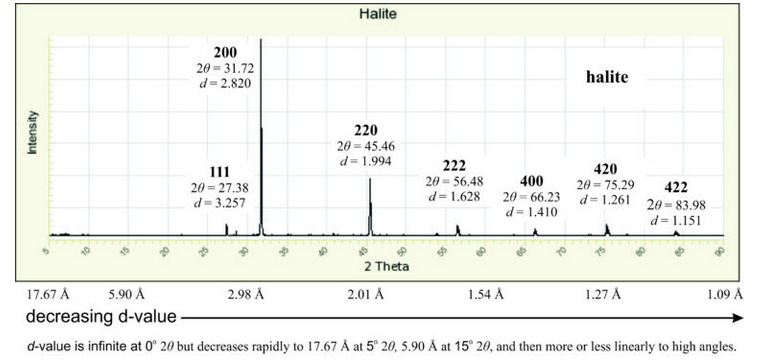
12.24.jpg — Figure 12.24: Copy and Paste Caption here. (Copyright; author via source)

The peaks in Figure 12.24, also called reflections, are labeled with the 2θ angles at which diffraction occurs. They are also labeled with associated hkl indices, called Laue indices, and d-values. By convention, when talking about diffraction directions, we use Laue indices with no parentheses (because we are labeling a reflection and not a family of planes) as is done in this figure. Note that, according to Bragg’s Law, the peak labeled 222 (at 56.48^o) in Figure 12.24 may be due to 1st-order diffraction by (222) planes (that have a spacing of 1.628 Å). However, 2nd-order diffraction by (111) planes (that have a spacing of 3.257 Å) also occurs at the same angle (discussed at the end of section 12.1.5, above). Higher-order diffraction from other families of planes, too, can cause diffraction at 56.48^o. Because we have no way to distinguish 1st-order from higher-order diffraction, we label the peak 222, assuming 1st-order. So, Laue indices are not the same as Miller indices, but are close.

We always assign the strongest peak an intensity of 100% and calculate other intensities compared with that peak. In this pattern, halite’s 200 peak at 31.7^o is most intense (100%). The 220 peak (45.5^o) is about 35% as intense, and other peaks are all small. Minerals with high symmetry, such as halite (which is cubic), generally have fewer than 30 measurable reflections in their powder patterns. Minerals of low symmetry have more.