11.3.3: How May Motifs and Lattices Combine?

Above, we saw examples where the lattice, the motif, and the overall pattern had the same symmetry. This was true in Figures 11.23, 11.24, 11.25, and 11.26. But, it was not true in Figure 11.27 where the motif and a primitive unit cell consisted of 3 atoms and a mirror plane of symmetry, while the lattice and overall pattern have hexagonal symmetry. Notice that in Figure 11.27, we could choose a triply primitive unit cell that had the same symmetry as the lattice and overall pattern. Because the triply primitive cell shows the 6-fold symmetry, it is the best choice.

This leads to an important second law of crystallography:
blank■ If a motif has certain symmetry, the lattice must have at least that much symmetry.

A motif with a 4-fold axis of symmetry requires a square plane lattice because it is the only plane lattice with a 4-fold axis. A motif, however, may have less symmetry than a lattice. If a motif has a 2-fold axis of symmetry, it may be repeated according to any of the five plane lattices because they all have 2-fold axes of symmetry.

Figure 11.28: Lattice, motif, and structure of halite

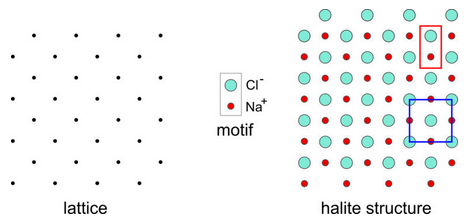
Halite (NaCl) is an excellent example of a mineral in which the simplest motif has less symmetry than the lattice. Figure 11.28 shows a two-dimensional model of the atomic arrangement in halite. The lattice is on the left and the motif, consisting of a Cl^– anion and an Na⁺ cation is shown in the center of the figure.

In two dimensions the lattice has square symmetry (although it is tilted to 45^o in this drawing), but the motif, consisting of one Na and one Cl atom, does not. Putting a motif at every lattice point gives the atomic arrangement on the right. A primitive unit cell (P), containing two atoms (outlined in red), is rectangular and does not have square symmetry. Notice, however, that we can choose a nonprimitive unit cell containing four atoms and two motifs (outlined in blue) that has square symmetry. This would not be possible if the lattice did not have “at least as much symmetry as the motif.”

Figure 11.29: An impossible combination of a lattice and a motif

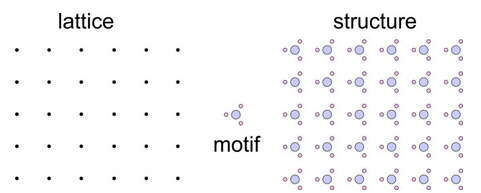
Figure 11.29 shows an impossible combination of a lattice and a motif. The lattice has 4-fold rotational symmetry, the motif has 3- fold symmetry. But the combination yields a structure that has no rotational symmetry. Looking at this figure should give you the sense that something is wrong. And, it is. If the motif really has 3-fold symmetry, it is identical in three directions 120^o apart. So bonds around it should be the same in three directions 120^o apart. But, they are not in the structure drawing. A motif with 3-fold symmetry requires a lattice that has at least 3-fold symmetry. There is only one and it is a hexanet. The lattice cannot be a square lattice.

So, motif symmetry and lattice symmetry both vary, but they cannot combine in an infinite number of ways because motif symmetry requires certain symmetry of the lattice. In fact, there are only 17 possible combinations in two dimensions. These are the 17 plane symmetry groups, discussed and depicted below in Box 11-1.

The 17 Plane Symmetry Groups

Figure 11.30: Three examples of glide planes

An atomic motif may have symmetry consisting of the standard symmetry operators: 1-fold, 2-fold, 3-fold, 4-fold, 6-fold rotation axes, and mirror planes. Lattices may have the same symmetry, and they also have translational symmetry.

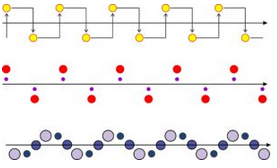
Additionally, there is one other kind of symmetry operation present in two-dimensional atomic arrangements: glide planes. Figure 11.30 shows three examples of a motif repeating by a glide plane. Think of the glide planes and atom repetition continuing indefinitely into space.

In each example in the figure above, the motif is translated before being reflected across the plane. Glide planes are one kind of symmetry operation that combines translation with point symmetry. Screw axes are another related operator that combines translation with point symmetry, but they do not exist in two dimensions. We will talk about both in more detail later in this chapter when we return to three dimensions and discuss space groups. For now it is sufficient to know that glide planes exist.

In two dimensions, atomic arrangements may have one of 17 possible symmetries. The drawings below show the possibilities. For each of the 17, larger patterns are shown with individual unit cells below. In the labels:
●P indicates a primitive cell; C indicates a centered (non-primitive) cell
●1, 2, 3, 4, and 6 designate rotation axes present
●m and g designate mirror planes and glide planes, respectively
●if the m (or g) symbol repeats (e.g., mm) it means that there are two differently oriented mirrors or glide planes of symmetry in the pattern

Figure 11.31: The 17 possible plane symmetries

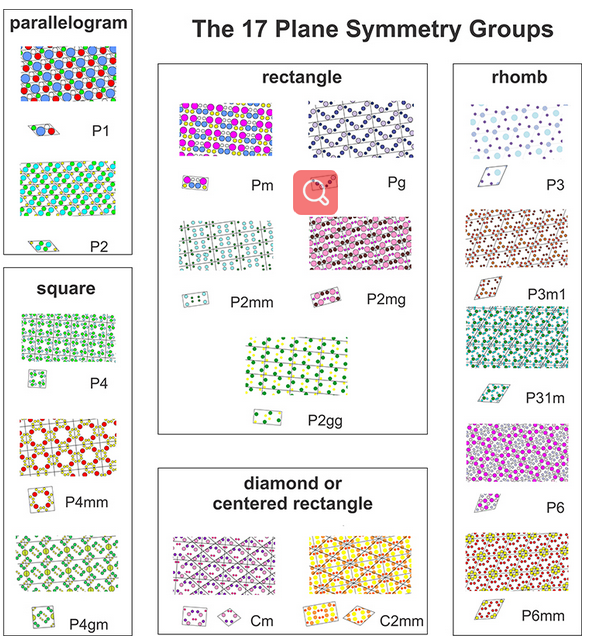
Three of the 17 possibilities involve square unit cells, seven involve rectangular unit cells. Of those seven, two are centered cells and the overall pattern could be made with a primitive diamond-shaped unit cell (also shown) instead of a rectangle. Two of the symmetry groups have unit cells shaped like a parallelogram, and five have rhomb-shaped unit cells. The rhomboid cells could be combined to produce non-primitive hexagonal cells. Some of the rhomb-based symmetry groups (the bottom two on the right) have 6-fold symmetry and some do not.