11.3.2: What are the Possible Plane Lattices?
- Page ID
- 18395
Above we looked at a number of different examples of lattices and unit cells. To get a complete list of possibilities let’s look at all the possible plane lattices. In a plane lattice, lattice points are related by two vectors describing translation. The vectors may be orthogonal (perpendicular to each other) or not. And they may be equal length or not.
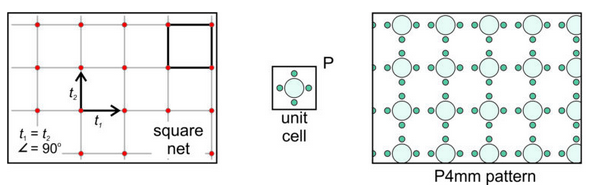
Square Net: Let’s consider the simplest possibility – that the vectors are orthogonal and of equal length. This produces a square net (lattice), as shown on the left in Figure 11.23, below. If we choose a square unit cell and put a motif (five atoms) with square symmetry within it, we get the pattern seen in the drawing on the right. This pattern has the same symmetry as the lattice and of the unit cell. The symmetry includes 4-fold and 2-fold rotation axes, and mirror planes that intersect at 45o and 90o. The P next to the unit cell reminds us that it is primitive. Because the overall atomic arrangement contains a 4-fold axis and two differently oriented mirrors (ones that are perpendicular to the faces of the unit cell, and ones that follows the diagonal of the unit cell), we describe its symmetry as P4mm.
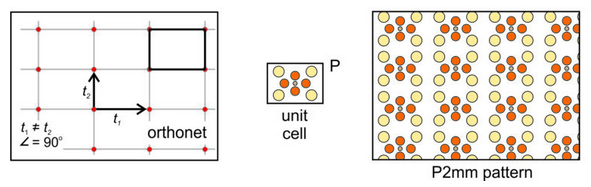
Orthonet: Suppose the two vectors relating lattice points are orthogonal but not of equal length. If so, we get an orthonet, equivalent to a rectangular lattice. Figure 11.24, below, shows an example. We can choose a rectangular unit cell and add a rectangular motif that contains nine atoms. We get the pattern shown on the right in Figure 11.24. Note that the lattice, the primitive (P) unit cell, and the pattern have equivalent symmetry that includes mirror planes and 2-fold rotation axes. The overall atomic arrangement contains a 2-fold axes with horizontal and vertical mirrors; we describe its symmetry as P2mm.
Diamond Net: A third general possibility is that the vectors relating lattice points are of equal magnitude but intersect at a non-special angle. This combination produce a diamond net (lattice) like the one below in Figure 11.25. We can add a motif of six atoms to a diamond-shaped unit cell to get the atomic arrangement shown on the right in Figure 11.25. But, notice that we can also choose a rectangular unit cell that is doubly primitive – it has an extra lattice point at its center and contains two motifs. Either unit cell will generate the same pattern. We use the letter P to indicate the primitive unit cell, and the letter C to indicate the cell with an extra lattice point in its center. The rectangular unit cell shows the vertical and horizontal perpendicular mirror planes and the 2-fold rotation axes more clearly than the diamond shaped one. So, we describe the symmetry of the pattern as C2mm.
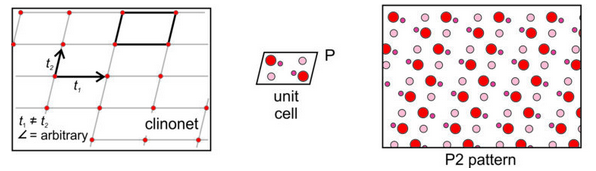
Clinonet: The fourth possibility is that the two translation vectors are of different lengths and are not orthogonal. This produces a clinonet (Figure 11.26) that corresponds to a primitive unit cell with the shape of a parallelogram. Adding a motif containing six atoms gives us the atomic arrangement on the right in Figure 11.26. There are no mirror planes here – the only symmetry is 2-fold rotation perpendicular to the page. The arrangement of atoms has symmetry P2.
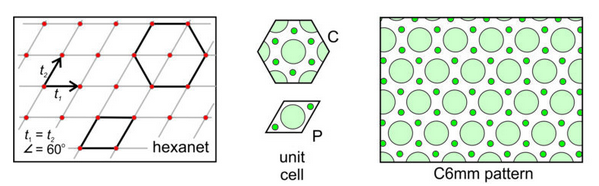
Hexanet: The fifth possible net is the created by the special case when the two translation vectors are of equal magnitude and intersect at 60o. This combination gives us a hexanet (hexagonal lattice) like the one shown in Figure 11.27, below. As with the diamond net, we can choose either a primitive rhomb-shaped unit cell or a triply-primitive hexagonal unit cell. The lattice and the overall atomic arrangement have hexagonal symmetry, so the hexagonal unit cell (which also has hexagonal symmetry) is generally chosen. A 6-fold axis and two kinds of mirrors at different orientations characterize this pattern. One set of mirrors is perpendicular to the faces of the hexagonal unit cell; the other passes through the corners of the unit cell. We designate the overall symmetry as C6mm.
