11.3.1: Motifs and Unit Cells

Last updated
Save as PDF

Page ID: 18394

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We can think of atomic arrangements as starting with one motif. The motif is then reproduced by translating (moving) it a certain distance and reproducing it. The distance of the translation is the distance between lattice points. If a dot replaces each motif, we get the lattice.

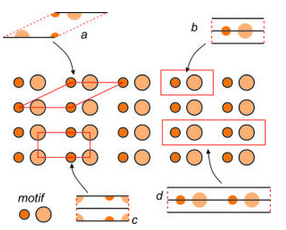
11.20.jpg — Figure 11.20: A motif with two atoms and some possible unit cells

Figure 11.20 shows a pattern made of two atoms, symbolized by different sized orange circles. The entire pattern consists of motifs composed of one of each kind of atom. The pattern contains multiple horizontal mirror planes but no other symmetry.

The figure shows several possible choices of unit cells (labeled a through d). In the individual unit cell drawings, solid black lines show mirror planes of symmetry.

Unit cells a, b, and c contain only one motif in total (one small orange circle and one larger lighter orange circle). We call them primitive because they are the smallest unit cell choices possible. All primitive unit cells contain exactly one motif, but atoms within a primitive unit cell may be in parts as in unit cell c. Add up the parts and you get one motif. We term unit cell d doubly primitive because it contains two motifs. Triply primitive unit cells contain three motifs, etc.

We can always choose a primitive unit cell for a repetitive pattern of atoms, but sometimes a primitive cell does not show symmetry clearly. By convention, we usually choose the smallest unit cell that contains the same symmetry as the entire pattern or structure. In Figure 11.20, unit cell b would be the choice of most crystallographers because it is simple, primitive, does not contain any partial atoms, and contains a horizontal mirror plane (which is the same symmetry as the entire pattern). Note that unit cell a, while also being primitive, does not have a mirror plane of symmetry within it; the other choices do.

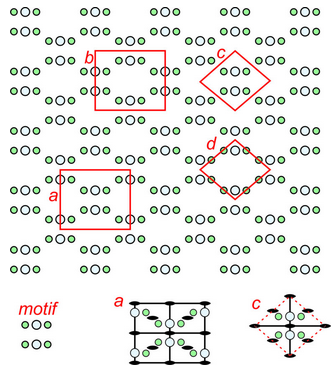
11.21.png — Figure 11.21: Motifs and unit cells with orthorhombic symmetry

11.22.png — Figure 11.22: Motif’s and unit cells with rhombohedral or hexagonal symmetry

The pattern shown in Figure 11.20 has relatively simple symmetry; the patterns in Figures 11.21 and 11.22 have more. Figure 11.21 shows an orthogonal (containing lots of 90^o angles) arrangement of atoms. The repeating motif contains six atoms – four green and two larger light blue ones. The letters a, b, c, and d designate four possible choices for unit cell. Cells c and d are primitive, containing six atoms total, although some are on the edges in cell d so only half of each green atom is in the unit cell. Cells a and b are doubly primitive but they are rectangular shapes. The symmetries of two of the unit cells are shown in the bottom of the figure. Solid black lines designate mirrors and lens shapes designate 2-fold axes. Unit cell a, although being double primitive, is the one that best shows the symmetry elements and so would be the choice of most crystallographers.

Figure 11.22 shows an overall hexagonal pattern. The motif consists of one large turquoise atom and two smaller green atoms. Four possible choices for unit cells are shown. Drawings in the bottom of the figure show symmetry of two of the potential unit cell with solid black lines as mirrors, lens shapes as 2-fold axes, and hexagons as 6-fold axes. Two of the potential unit cells are rhomb shaped and two are hexagonal. Because the overall pattern has hexagonal symmetry, unit cells c and d are preferred choices compared with the other two. Unit cell d is primitive, but does not include all the symmetry. (It does not have 2-fold rotation axes.). So cell c is the best choice. This pattern demonstrates why we treat rhombs with 60̊^oand 120̊^oangles at their corners as special cases – they sometimes result in hexagonal symmetry while diamonds with general angles at their corners cannot.

Although crystallographers follow standard conventions, they are often forced to make choices. If they choose primitive unit cells, each lattice point corresponds to one unit cell and one motif. If they choose nonprimitive unit cells, lattices represent the way motifs repeat, but not the way unit cells repeat because there is more than one lattice point per unit cell.