10.4: Combinations of Symmetry Elements- Point Groups

Because some symmetry operators are redundant, we do not need them all to describe the symmetry of crystals. By convention, crystallographers use the 13 operators listed in the table seen here. In mathematical terms, these 13 are sufficient to describe symmetry in any crystal.

These symmetry operators can combine, so more than one can be present in a crystal. But, the number of possible combinations is limited for two reasons. First, some combinations lead to other symmetry. Second, some combinations are contradictory and thus impossible.

symmetry operators

i m = 2 = ^1/m 1 2 3 4 6 3 4 6 = ^3/m ^2/m ^4/m ^6/m

Figure 10.40: Three 2-fold axes

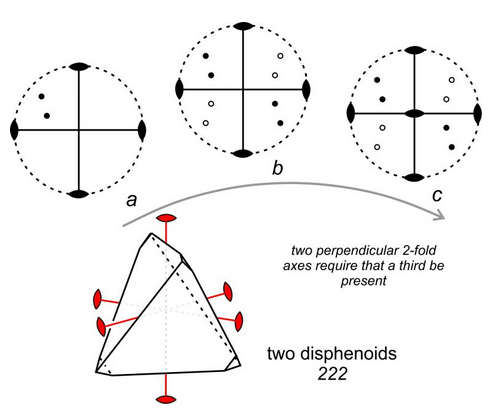
Consider, for example, a crystal that has two 2-fold axes of symmetry that intersect at 90^o , as depicted in Figure 10.40. If we start with dots representing two faces (diagram a), application of the symmetry operators produces six more dots/faces (diagram b). Four of the faces are above the page and four below. Diagram b reveals that a third 2-fold axis is perpendicular to the original two, shown by a lens shape at the center of diagram c. Thus, we see that all objects that have two perpendicular 2-fold axes of symmetry must have a third 2-fold axis. It does not matter which two 2-fold axes we choose initially; the third must be there. Figure 10.40 reinforces what we concluded earlier – that symmetry operators operate on each other.

The symmetry depicted in Figure 10.40 consists of three mutually perpendicular 2-fold axes. We use the shorthand notation 222 to describe this symmetry. The drawing in the bottom of Figure 10.40 is only one of many possible crystal shapes that have 222 symmetry. The three 2-fold axes (shown in red) pass through the centers of edges of the crystal. Four faces related by 222 symmetry make up a disphenoid. The crystal depicted contains two forms; both are disphenoids. The four faces of one form are, however, quite small and just show at the corners of the crystal.

We call distinct combinations of symmetry, such as 222, point groups. So, the crystal in Figure 10.40 belongs to point group 222. Figure 10.36 showed a crystal that belonged to a different point group, ²/_m. Point groups describe symmetry around a point in the center of a crystal, and thus they relate the points in a stereo diagram to each other. The word group is used because we may treat the principles of symmetry using mathematical group theory. The terms operator and operation also derive from group theory. In group theory, the 13 operators listed in the table above form a basis, which means we need no other operators to describe all possible manifestations of symmetry.

Figure 10.41: 2-fold axes intersecting at 60̊

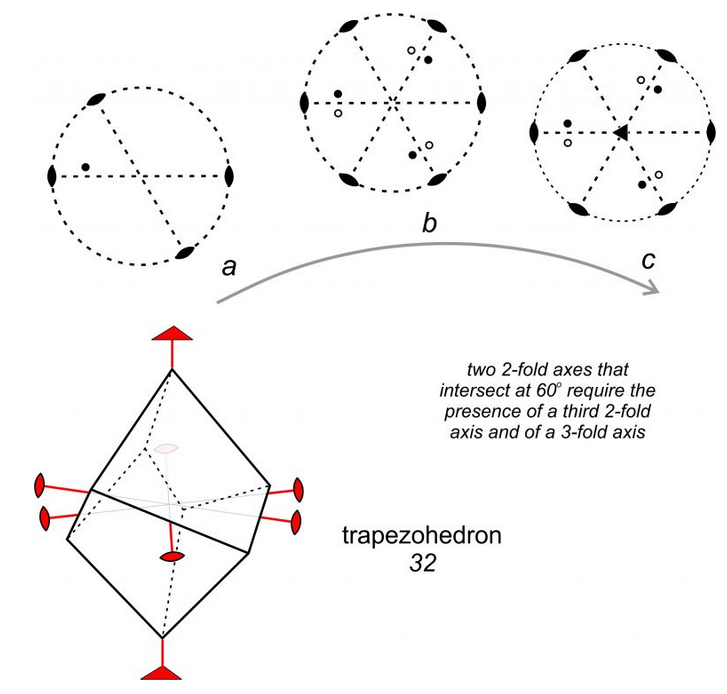
Figure 10.41 shows another example of symmetry operators acting on each other. Two 2-fold axes intersect at 60^o (diagram a). Starting with one point and applying the symmetry operators, we soon generate five more equivalent points (diagram b). Examination of the resulting pattern shows that a third 2-fold axis lies at 60° to the first two. Additionally, a 3-fold axis (shown by a triangle at the center of the diagram) is perpendicular to the two folds (diagram c). Another way of looking at the symmetry in Figure 10.41 is to notice that the 3-fold rotation axis acts on the 2-fold axes. It requires that if one 2-fold axis of symmetry is present, two others must be present as well, and that the three are related by angles of 120°. The point group for this symmetry is designated 32. The drawing in the bottom of Figure 10.41 shows a crystal that has 32 symmetry. It is a trapezohedron, named after the shapes of its faces.

In Figure 10.40 we showed that two perpendicular 2-fold axes required the presence of a third mutually perpendicular one. In Figure 10.41, we showed that if two 2-fold axes intersect at 60°, another 2-fold and a 3-fold will also be present. Similarly, if we start with a 4-fold axis and one perpendicular 2-fold, we will find other 2-folds perpendicular to the 4-fold and at 45° to each other. If we start with a 6-fold axis and a perpendicular 2-fold, we will find six 2-fold axes in all.

Figure 10.42: Crystals belonging to point groups 222, 32, 422, and 622

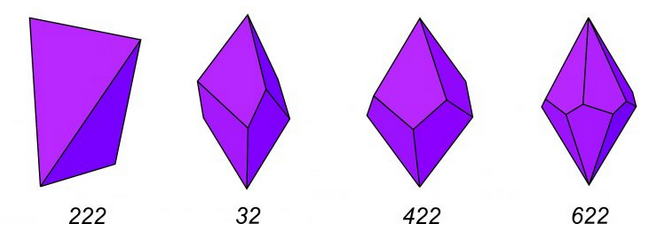
Figure 10.42 shows drawings of crystals belonging to point groups 222, 32, 422, and 622. Note that mirror planes are absent in all four cases. The top and bottom of the crystals do not mirror each other, and the crystal faces do not have mirror planes down their centers or edges (or else an m would be included in the symbol for the point group). The four examples point out that symmetry operators cannot combine in random ways. The presence of two rotation axes requires a third and perhaps more. We can also show that a combination of a rotation axes and a mirror, at angles other than 0° or 90° to each other, requires other rotation axes to be present. Seeing symmetry on the complicated crystal drawings in Figure 10.42 is difficult. (That’s why we have stereo diagrams!) A better way to examine symmetry of crystals is to study models in the laboratory.

Figure 10.43: 4/m 2/m 2/m symmetry

Before leaving this discussion about the way symmetry combines to produce other symmetry, let’s consider one more example. Figure 10.43a shows points related by a 4-fold rotation axis. We can add a horizontal mirror (shown by the solid outer circle) to produce the points shown in diagram b. Adding a vertical mirror produces diagram c. And, in diagram c, we see that this is equivalent to symmetry that includes a 4-fold axis and two different kinds of 2-fold axes (shown in diagram d). All the rotation axes are perpendicular to mirror planes. This is point group ⁴/_m²/_m²/_m.