10.4.1: Special Angles and General Angles

Last updated
Save as PDF

Page ID: 18478

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Angles such as 30°, 45°, 60°, 90°, or 120° are called special angles. They all divide evenly into 360°. We call nonspecial angles general angles. In the examples in Figure 10.43, and others considered previously, we started with rotation axes and mirror planes that intersected at special angles. Suppose we start with axes or mirrors that intersect at general angles. What will be the result?

10.44.png — Figure 10.44: Infinite symmetry is not possible

The first diagram in Figure 10.44 shows two intersecting 2-fold axes and three points related by them. The angle between the axes is small and does not divide evenly into 360°. It is a general angle. We may apply the 2-fold axes to each other to generate more 2-fold axes and points, moving around the diagram in a stepwise manner as shown. We could do this forever, continuing around the circle indefinitely, because the new axes and points we generate will never coincide with others already present. When we continue this operation all the way around the circle, we will not end back where we started. So, the number of 2-fold axes becomes infinite, and an infinite-fold axis of symmetry must be perpendicular to the plane of the page. This is equivalent to the symmetry of a circle. Since crystals consist of a discrete number of faces (and atomic arrangements consist of a discrete number of atoms), we know that infinite symmetry is not possible. We may therefore conclude that if crystals have two 2-fold axes, they must intersect at a special angle so that they are finite in number.

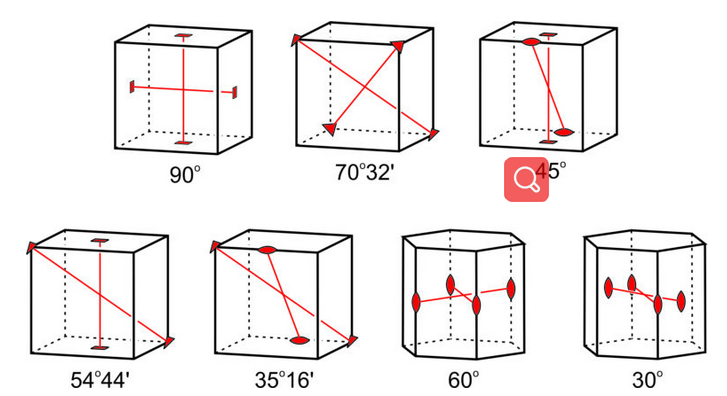
10.45.png — Figure 10.45: Possible intersection angles for rotation axes

The preceding discussion suggests that rotation axes only combine in a limited number of ways. In fact, angles between rotation axes are limited to the seven depicted in Figure 10.45. We have already seen examples of each. These drawings are of a cube and a hexagonal prism, but angles between rotation axes in crystals of other shapes are limited to the same seven values. The possible angles between rotation axes are all special angles. If we carried out the exercise, we would find that in crystals with both rotation axes and mirror planes, the angles between the rotation axes and the mirror planes are limited to only a few special angles as well. Otherwise, we have infinite symmetry. In most crystals the angles are 0° (the rotation axis lies within the plane of the mirror) or 90° (the rotation axis is perpendicular to the mirror).