10.3.1: Special Forms and General Forms

Last updated
Save as PDF

Page ID: 18475

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Diagrams e, f, and g in Figure 10.33 show stereo diagrams with points corresponding to the faces on a cube, octahedron, and dodecahedron. Cubes, octahedra and dodecahedra are special forms, and the points on the stereo diagram are called special points, because the faces/points coincide with symmetry elements. (For example, cube faces are perpendicular to 4-fold rotation axes.)

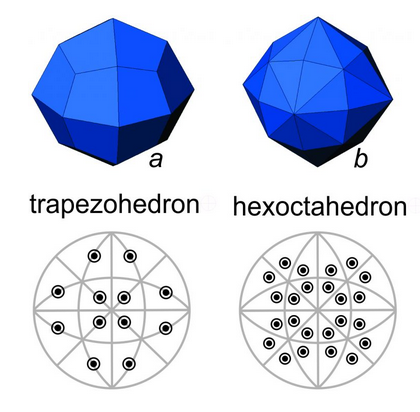
10.34.jpg — Figure 10.34: Trapezohedron and hexoctahedron

Besides the cube, octahedron and dodecahedron, other special forms have cubic symmetry. For example, Figure 10.34a shows a trapezohedron. As seen in the diagram beneath the crystal drawing, trapezohedron faces lie on (are perpendicular to) mirror planes. So, a trapezohedron is also a special form.

The hexoctahedron in Figure 10.34b, however is the general form that has cubic symmetry. It has the maximum number of faces for minerals with cubic symmetry (48) and the faces are neither parallel nor perpendicular to any symmetry elements (mirrors or rotation axes). No matter what the symmetry, the general form always has more faces than any special form.

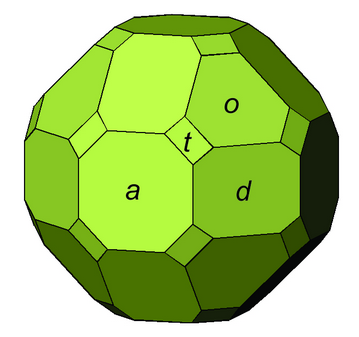
10.35.png — Figure 10.35: A crystal containing cube (a), octahedron (o), dodecahedron (d), and trapezohedron (t) faces.

The examples of cubic crystals just seen (in Figures 10.33 and 10.34) contain a single form. But, cubic crystals commonly contain multiple forms. The crystal in Figure 10.35 is an example. It contains four forms: cube, octahedron, dodecahedron, and trapezohedron. This crystal contains four different shaped faces, one corresponding to each form; they are labeled with different letters. In all, the crystal has 38 faces. Yet, the symmetry of this crystal is the same as the crystals seen in the previous two figures.