1.4: EMR interactions with the Earth’s atmosphere and surface
- Page ID
- 17275
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After electromagnetic radiation has been created by the Sun, the part of it that has found its way through the vacuum of space to the top of the Earth’s atmosphere must pass through the atmosphere, be reflected by the Earth’s surface, pass through the atmosphere again on its way back to space, and then arrive at the sensor in order to be recorded. While nothing happens to the radiation field as it passes through empty space, several things happen as it interacts with the Earth’s atmosphere and surface. It is due to these interactions that the measured radiation ends up containing information about the Earth environment, so it is important to take a closer look at exactly what happens in these interactions, and how it affects the radiation field.
Interactions with the atmosphere
The interaction between electromagnetic radiation and the Earth’s atmosphere can be considered to have three components: refraction that changes the direction of propagation of the radiation field due to density differences between outer space and the atmosphere, scattering that changes the direction of propagation of individual photons as they are absorbed and re-emitted by gasses or aerosols or other atmospheric constituents without changing wavelength, and absorption that convert photons into vibrations in a molecule, energy which is (later) re-emitted as one or more photons with longer wavelength(s). Each will be considered in more detail below.
Refraction
Refraction is the bending (and slowing down) of the direction of propagation of electromagnetic radiation as it moves between two media with different densities. This happens as radiation arrives from outer space (density ≈0) and enters the atmosphere (density >0). The angle at which the direction of propagation changes is determined by the refractive indices of the two media. The refractive index of a medium (n) is determined as the ratio of the speed of electromagnetic radiation in a vacuum (c) to the similar speed in the medium (cn): n=c/cn. The refractive index of a standard atmosphere is 1.0003, while the refractive index of water is 1.33. Using the refractive indices of the two media, the amount of refraction can be determined with Snell’s Law: n1 * sinΘ1 = n2 * sinΘ2.
where n are the refractive indices of the two media and Θ are the angles at which the direction of propagation intersects the normal of the surface separating the two media (Figure 22). Refraction is rarely a relevant factor in the practical use of remote sensing data. Its only important influence concerns the georeferencing of imagery collected when the Sun is close to the horizon, and this is a problem that is nearly always dealt with by the image provider. One important situation in which refraction is important and must be considered is when an image analyst needs to precisely geolocate underwater objects (such as features on the seafloor in coastal areas).
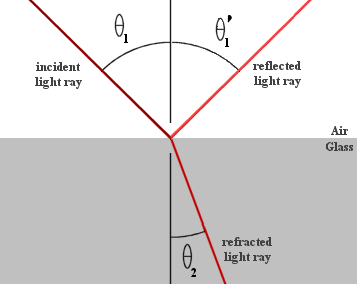
22: Refraction according to Snell’s Law. While this image illustrates refraction of light passing from air to glass, the same principle applies to the air-water interface. Example snells law by RJHall, Wikimedia Commons, CC BY-SA 2.0 AT.
Scattering
One of the two remaining processes that influence electromagnetic radiation as it passes through the atmosphere is scattering. Scattering happens when a photon interacts with something in the atmosphere that causes it to change direction. Depending on the size of the object that the photon interacts with, two distinct types of scattering are recognized. Rayleigh scattering happens when the object is much smaller than the wavelength of the radiation. In the case of sunlight and the Earth’s atmosphere this means that Rayleigh scattering is cause by atmospheric gasses like N2, O2, CO2 etc. Mie scattering happens when the object is similar in size to the wavelength of the radiation, which means that it is caused by aerosols like smoke and dust particles. Additional scattering can happen if radiation interacts with particles larger in size than its wavelength, like water droplets or sand particles.
While refraction is predictable and can be determined by Snell’s Law, scattering is an inherently stochastic process: what happens to an individual photon as it passes through the atmosphere is entirely unpredictable, including whether or not it experiences any scattering, and if so which direction it is reemitted in. However, the magnitude and direction of scattering that happens on average to the many photons in a radiation field is predictable.
Rayleigh scattering
A fact that has great importance for remote sensing of the Earth is that the magnitude of Rayleigh scattering is inversely related to the 4th power of the wavelength of the radiation. In other words, radiation with shorter wavelengths is scattered much more by Rayleigh scattering than radiation at longer wavelengths. In the visible wavelengths, this means that blue light is scattered more than green light, which in turn is scattered more than red light. This is the process that makes the Earth’s oceans look blue when viewed from space. What happens is that over very dark Earth surfaces, such as the oceans, the majority of radiation reaching the Earth surface is absorbed rather than reflected by it. What is visible from space is thus not radiation reflected by the surface, but rather radiation scattering from within the atmosphere. Because blue wavelengths are those most strongly scattered through Rayleigh scattering, this scattered radiation as a whole looks blue (Figure 23). Another effect of Rayleigh scattering is that regardless of what is on the Earth’s surface, a space-based sensor will detect a substantial amount of blue light coming from the Earth-Atmosphere system. This can be a problem because the ‘blue signal’ form the atmosphere overwhelms variations in ‘blue reflectance’ on the surface. But it can also be an advantage, because measurements in the blue wavelengths can help assess the strength of Rayleigh scattering across the visible and infrared spectrum, which can in turn be corrected for. This is the basis for the ‘aerosol’ band that was included on Landsat 8 OLI (but was not found on its predecessor instruments), on Sentinel-2, and on the WorldView-2 and -3 sensors.

23: Earth from space. The Blue Marble (globe west) by Reto Stöckli, Visible Earth (NASA), Visible Earth Image Use Policy.
While any scattering in the atmosphere is a source of noise (for those interested in using satellite imagery to characterize the Earth’s surface), Rayleigh scattering is a relatively benign source of noise because its wavelength dependence makes it largely predictable, and because the gasses responsible for it tend to have stable concentrations across space and time. Rayleigh scattering is therefore not a source of great uncertainty for most remote sensing applications.
Mie scattering
Mie scattering, because its strength and wavelength dependence depends on the type and density of the particulates that cause it to happen, varies substantially through time and space. As a result it is one of the most important causes of uncertainty in remote sensing, especially when using satellite data to study dark parts of the Earth’s surface from which the amount of reflected radiation is small relative to the total signal from atmospheric scattering. For the same reason it is hard to generalize its importance, but broadly speaking the strength of Mie scattering exceeds that of Rayleigh scattering, and while it still diminishes with increasing wavelength its influence extends further into the infrared spectrum. Because Mie scattering is caused by atmospheric particulates, it is often dramatically increased during dust storms, forest fires, or other events that caused the atmospheric aerosol load to increase. One such example is seen in Figure 24.

24: Greatly increased Mie scattering caused by forest fires in Australia, 2009. Smoke clouds by Warren, Flickr, CC BY-NC-SA 2.0.
Absorption
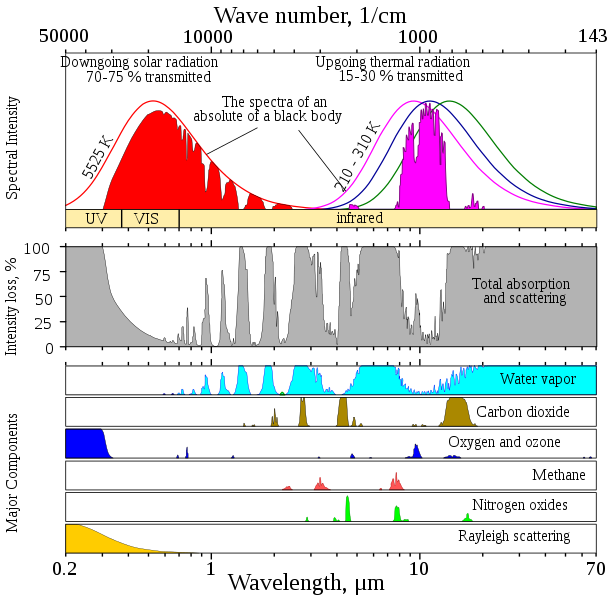
The last important thing that happens to electromagnetic radiation as it passes through the atmosphere is that it is partially absorbed by atmospheric gasses (mostly H2O, CO2 and O3). While the energy absorbed is ultimately re-emitted by these gas molecules, the re-emission happens at wavelengths typically outside the spectrum considered in optical remote sensing (but which may be important for thermal remote sensing), so for practical purposes the absorbed photons can be considered gone when absorbed. The strength of absorption is highly dependent on wavelength because it happens most easily when the radiation has a wavelength (frequency) that is similar to a resonant frequency of the gas doing the absorption, which in turn depends on its atomic or molecular structure. For example, due to its molecular structure, O2 is particularly good at absorbing electromagnetic radiation with wavelengths right around 760 nm, but not at 750 or 770 nm. Similar wavelengths exist at which other gasses are effective or not at absorbing EMR, and in combination the atmospheric gasses let some wavelengths pass through the atmosphere with almost no absorption, while other wavelengths are almost entirely absorbed before they reach the surface of the Earth (Figure 25 and Figure 26). As is especially clear in Figure 26, water vapour is responsible for much of the total gaseous absorption of EMR in the atmosphere, including in the visible spectrum (not clearly shown on that figure). This is an important challenge for remote sensing because while the concentrations of the other gasses are relatively stable through time and space, water vapour concentrations vary greatly through time (humid vs. dry days) and through space (dry arctic vs. humid tropical).
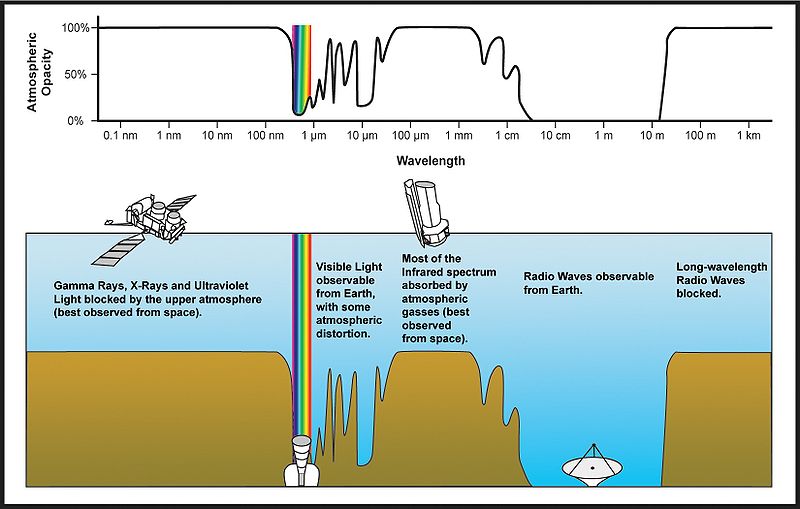
25: Atmospheric opacity by wavelength across the electromagnetic spectrum. Atmospheric electromagnetic transmittance or opacity by Edwtie, created by NASA, Wikimedia Commons, public domain.
Interactions with the surface
The part of the radiation field that has made it through the atmosphere without being absorbed or scattered back toward space now reaches the Earth’s surface. For any wavelength that is of relevance to remote sensing, only one of two things can now happen to each individual photon – it can be absorbed by the Earth’s surface, or it can be reflected back toward space. The probability of reflection rather than absorption happening is termed the reflectance of the surface, and it depends on the material on the surface as well as the wavelength of the incoming radiation. Each surface material has a unique ‘signature’ that defines what proportion of radiation is reflected for each wavelength. For example, water reflects a small amount of blue and green wavelengths (typically around 5% – 10% depending on turbidity), less of the red wavelengths, and almost nothing in the infrared wavelengths. Vegetation, on the other hand, reflected around half of all incoming infrared radiation, except for specific wavelengths that are effectively absorbed by liquid water in the leaves. These spectral signatures are commonly portrayed as graphs, with wavelengths along the x-axis and reflectance along the y-axis (as in Figure 27).
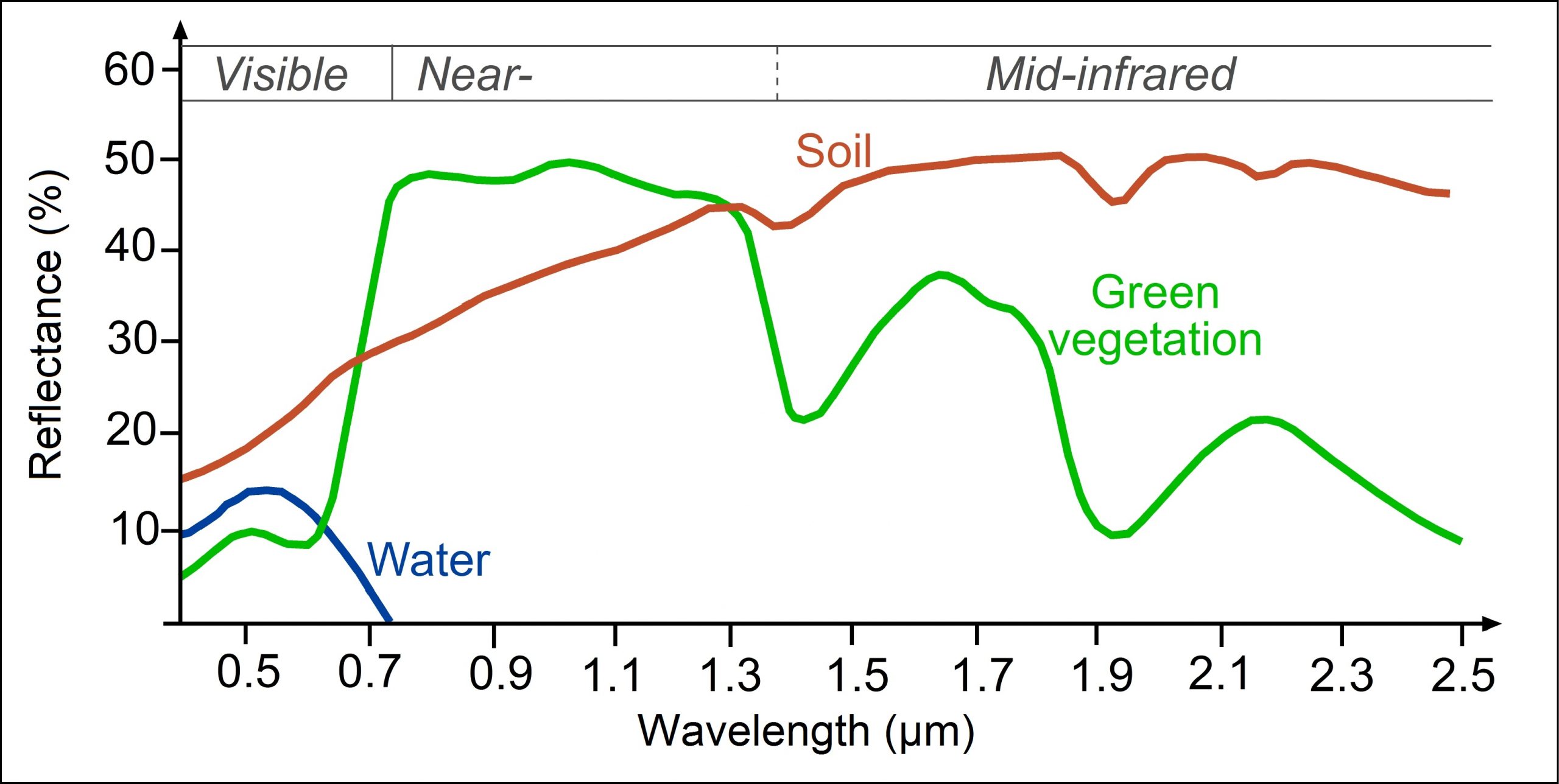
27: Spectral signatures of broadly defined common types of Earth surface materials. Reflectance of water, soil and vegetation at different wavelengths by Science Education through Earth Observation for High Schools (SEOS), CC BY-NC-SA 2.0.
Spectral signatures are what enables us to differentiate between different materials on the Earth’s surface when we look at a satellite image. As shown in Figure 27, water has near-zero reflectance at wavelengths longer than 0.7 μm (700 nm), while both soil and green vegetation has reflectances around 40% at 1.3 μm. Measuring the amount of radiation reflected off the Earth-Atmosphere system at 1.3 μm will thus be particularly helpful at differentiating water from the two terrestrial surface types. Similarly, measurements at wavelengths around 1.4 μm (where liquid water in vegetation is a strong absorber) or 1.9 μm (same) can be effective to differentiate between soil and green vegetation.
As a more detailed example, spectral signatures have been effective for large-scale geological surveying/prospecting because different minerals (that may be characteristic of different sub-surface conditions) can be identified through their unique spectral signatures (Figure 28).
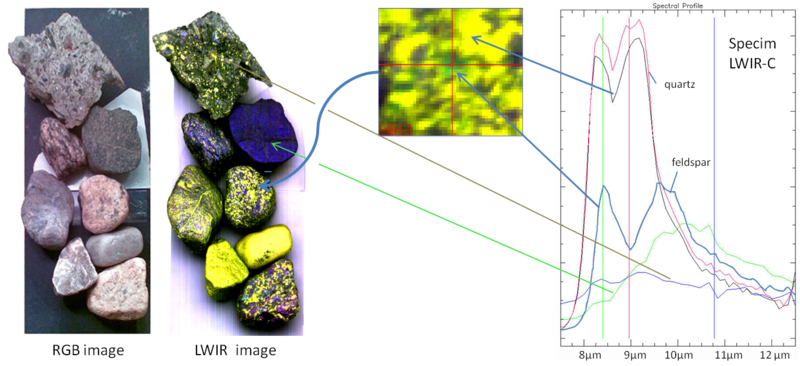
28: Examples of spectral signatures of minerals. HIS LWIR stones by Aappo Roos, Wikimedia Commons, CC BY-SA 3.0.
The part of the radiation field that is reflected by the Earth’s surface must naturally make its way back up through the atmosphere, with the attendant refraction, scattering and absorption, before it can be measured by any space-based sensor. While there are many relative advantages and disadvantages to air-borne vs. space-borne sensors, the ability of air-borne sensors to measure the reflected EMR field before it has had to pass through the atmosphere a second time is one distinct advantage.
Atmospheric correction
Unless you are an atmospheric scientist, the interactions between the electromagnetic radiation field and the Earth’s surface is the one important thing that is of interest to you in remote sensing, because that is what lets you use the measured radiation to infer something about the state of the Earth’s surface – whether it is covered in water or land, what minerals the surface is composed of, how healthy the vegetation is, or how much sediment is in the water. The fact that interactions also happen between the EMR field and the atmosphere, and that these interactions influence the intensity of radiation measured by the sensor at different wavelengths, is an important source of noise. One of the great and difficult challenges in remote sensing thus is to correct for the effect that the atmosphere has on the measured radiation, thus converting our measurements from a description of the Earth-Atmosphere system to a description only of the Earth’s surface. This process is called atmospheric correction. In practical terms, atmospheric correction is typically used to convert an estimate of TOA radiance or TOA reflectance to an estimate of surface reflectance. This conversion is important because it lets you make direct comparisons between the reflectances observed in different bands for a pixel and the spectral signatures measured on Earth such as those in Figure 27 and Figure 28.
There are different approaches to atmospheric correction, ranging from the very simple to the very complicated. The simplest approach is to employ the assumption that somewhere in the image you want to perform atmospheric correction for there is a pixel that is completely, perfectly, black, across the bands available in the image. This is called the ‘dark pixel assumption’. Strictly speaking this does not have to be a single pixel, one could also assume that at least one pixel has zero reflectance in band 1, one pixel (maybe the same pixel, maybe another one) has zero reflectance in band 2, and so on. Assuming that this is true, for each band, the pixel in the image with the least amount of radiance measured coming from it (i.e. with the lowest DN value) must be the zero-reflectance pixel, and whatever radiance is measured as coming from it must have originated from scattering in the atmosphere (because if it had reached the Earth’s surface it would have been absorbed by it). The hypothetical zero-reflectance pixel can thus give a first-order estimate of how much radiance originates from scattering in the atmosphere. Additionally assuming that this amount is constant throughout the image, the ‘atmospheric contribution’ can be subtracted from all pixels, leaving only what was reflected by the surface, called the ‘surface contribution’. Of course, the assumption of the existence of a perfectly black pixel in the image may not be true, and the atmospheric contribution may also not be the same everywhere, but as a method that can be applied without having any actual knowledge of the state of the atmosphere when the image was acquired, it is not a bad method.
The ‘dark-pixel’ method is an example of what is called image-driven methods of atmospheric correction. Other such methods make other assumptions, such as the presence of dense dark vegetation with typical spectral characteristics, or the presence of a range of surface types with known spectral signatures. These methods work reasonably well when their assumptions are met, but can fail spectacularly when they are not.
More sophisticated methods rely on some form of information about the state of the atmosphere at the time of image acquisition, typically the amount and type of aerosols and the amount of water vapour. With this information, numerical models that quantify the scattering and absorption and thus the transfer of radiation of different wavelengths through the atmosphere can be used to model the surface reflectance that must have existed, in combination with the known atmosphere, to produce the observed TOA reflectance. Some such methods do not require specific information on aerosols and water vapour, but rather need you to tell them what the visibility in the area was at the time of image acquisitions – since visibility is reduced with increasing amounts of water vapour in the atmosphere the methods can work out the water vapour and go from there. Atmospheric correction is a very active area of research in optical remote sensing, and modern satellite sensors are routinely designed to include measurement bands that help in an image-driven estimation of water vapour and aerosol load.
Almost all atmospheric correction methods make the fundamental assumption that the atmosphere is uniform within the satellite image considered. While this is obviously not perfectly true, it is often but not always a reasonable assumption. Hyperspectral sensors, which record radiation in many, often hundreds, of contiguous bands, have the ability to estimate water vapour and aerosols loads on a per-pixel basis, thus effectively mapping the atmospheric components contributing the greatest uncertainty, after which a per-pixel atmospheric correction can be applied.
The importance of atmospheric correction and the estimation of surface reflectance for each pixel is not just to enable comparison with field-measured spectral signatures, or to identify Earth surface materials. More fundamentally, its importance is due to the fact that surface reflectance is a fundamental physical property of the surface, and that it is not influenced by illumination conditions, sensor design, atmospheric state, or any of the other factors that differ between different images of the same area. For a pixel, an estimate of surface reflectance is thus directly comparable between images taken at different times, with different sensors, at different solar zenith angles, and under dry or humid, clear or smoky atmospheres. What this means is that an area can be monitored and in the absence of change the estimated surface reflectance (by band, i.e. the spectral signature) should not change – which in turn means that if the spectral signature is indeed seen to change through time, actual change is happening on the surface. Proper atmospheric correction is thus (with a few exceptions) the basis for a large field of applied remote sensing – detection of change.


