3.2: Soil Density

Last updated
Save as PDF

Page ID: 14722

Colby Moorberg & David Crouse
Kansas State University via Prairie Press

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Measure soil bulk density and calculate pore volume relationships.

The flow of liquids and through soil is essential for the existence of plants and other soil organisms. Those flows are dependent on soil porosity and pore connectivity. Soil porosity is also dependent on, and inversely related to, soil density. If a soil is compacted, the soil solids are packed into a smaller volume, and the particles get packed closer together. This results in less total pore volume. Thus as soil density increases, soil porosity decreases. Soil density is relatively simple and cheap to measure. This laboratory entails a demonstration of the use of a soil density sampler, and a problem set that is focused on common soil density calculations.

Materials

Soil bulk density sampler
Soil Density Problem Set

Introduction

Soil physical properties control the mechanical behavior of soils and will strongly influence land use and management. Several important physical properties have been discussed in other labs: texture, structure, color, and consistency. In this laboratory, additional physical properties will be measured, and their implications for land management will be discussed.

Bulk Density, Particle Density, and Pore Space

Soil represents a unique arrangement of solids and voids. The voids, or pore space, are important for air and water movement and storage. The total pore space consists of the voids between sand, silt, and clay particles and voids between soil aggregates. Therefore, texture and structure govern the amount of soil pore space. Organic matter affects the solids portion of the soil but also influences porosity indirectly through its effect on structure.

Density refers to a mass per unit volume. Bulk density of a soil refers to the mass of a volume of dry soil. The volume includes both solids and pores. Particle density refers to the mass of solids per volume of the solids alone. These two density measurements provide an important insight into the physical nature of a given soil. Soil density plays a major role both in plant growth and in engineering uses of soil. The formulas for calculating bulk density and particle density follow:

\[\text{Bulk density, }ρ_\text{b}=\frac{\text{mass of oven dry soil}}{\text{total soil volume}}\] \[\text{Particle density, }ρ_\text{p}=\frac{\text{mass of oven dry soil}}{\text{volume of soil solids}}\]

Figure 8.1. Uhland sampler for collecting soil samples for bulk density determinations. Diagram from King et al. (2003).

Units of density are typically expressed in g cm^–³ or Mg m^-3.

Note that total volume of the soil sample equals the volume of the solids and the volume of the pores.

Porosity is the ratio of the volume of the pores in a soil sample to the total volume of the sample:

\[\text{Porosity, }φ=\frac{\text{volume of pores}}{\text{total soil volume}}\]

However, measuring the volume of pores in a soil sample is difficult. In practice, porosity is normally calculated using the formula:

\[\text{Porosity, }φ=1-\frac{ρ_\text{b}}{ρ_\text{p}}\]

Porosity is usually expressed as a decimal, but it can also be expressed as a percentage by multiplying the decimal form by 100%.

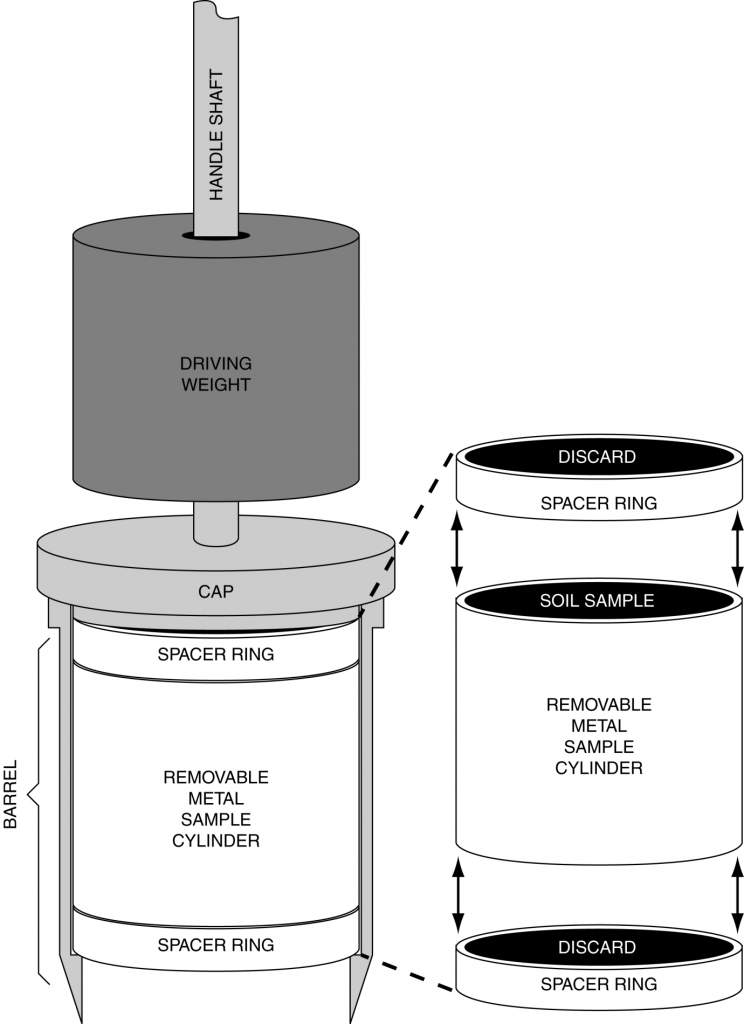
Samples for determining bulk density must be collected very carefully to insure the sample represents the in situ condition desired and no additional compaction or loosening has occurred. One method for determining bulk density is the “core” method. A (relatively) undisturbed, cylindrical soil core is collected using a device like the one shown in Figure 8.1.

The driving weight is raised and dropped repeatedly to drive the sampler into the soil. When the desired depth is reached, the device is removed from the soil, and the removable metal cylinder containing the soil sample is removed. With the dimensions of the cylinder and the weight of oven-dry soil inside the cylinder, we can calculate the bulk density.

Sampling Procedure

Insert a 1.5 cm metal ring, a 6 cm metal core, and then a second 1.5 cm metal ring into the barrel of the core sampler, then reattach the barrel to the handle. The sample will be held in the longer cylinder; the two 1.5 cm rings are spacers, which help ensure an undisturbed soil sample.
Place the sampler over the desired sampling location, and then drive it into the soil with the slide hammer at the top of the handle. Stop when the cap of the barrel is flush with the soil surface.
Remove the sampler from the soil by pushing against the handle until the vertical shaft of the handle is parallel to the soil surface.
Remove the barrel from the sampler and gently push the core out of the top of the barrel, taking care to keep the core intact.
Carefully cut between the two shorter rings and the main core. Place the core into a labeled, pre-weighed canister, and put on the lid.
Back in the lab, weigh each canister plus moist soil.
Determine the weight of dry soil in the sample.
Measure the length and diameter of the metal cylinders.
Use this information to calculate bulk density, porosity, and water-filled pore volume.

Determining the weight of dry soil in the sample

The simplest method is to dry the sample in a conventional oven:

Remove the lids of all of the canisters, and place each in a 105C oven. Dry overnight.
Record the final weight of each canister (including the lid) plus oven-dry soil.
Calculate the moisture content of the samples:

\[\text{Mass of water}=(\text{mass of beaker}+\text{moist soil})-(\text{mass of beaker}+\text{dry soil})\] \[\text{Mass of dry soil}=(\text{mass of beaker}+\text{dry soil})-\text{mass of beaker}\] \[\text{Percent moisture}=\frac{\text{mass of water in soil}}{\text{mass of oven dry soil}}\times100\text{%}\]

Calculate the dry weight of the soil in each cylinder and record the data:

\[\text{Dry weight}=\frac{\text{wet weight}}{1+(\frac{\text{percent moisture}}{100\text{%}})}\]

Activity 1 & Assignment: Problem Set

The problem set will be provided to you at the beginning of the laboratory session. You will be working with your classmates to complete it during lab. Your lab instructor will help you as needed.