5.3.3: A Classification of Faults
- Page ID
- 5918
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Overview
Most damaging earthquakes form on faults at a depth of five miles or more in the Earth’s crust, too deep to be observed directly. But most of these faults are also exposed at the surface where they may be studied by geologists. Larger earthquakes may be accompanied by surface movement on these faults, damaging or destroying human-made structures under which they pass.
Some faults are vertical so that an earthquake at 10 miles depth is directly beneath the fault at the surface where the rupture of the ground can be observed. Other faults dip at a low angle, so that the fault at the surface may be several miles away from the point on the Earth’s surface directly above the earthquake (Figure 3-4). Where the fault has a low dip or inclination, the rock above the fault is called the hanging wall, and the rock below the fault is called the footwall. These are terms that were first coined by miners and prospectors. Valuable ore deposits are commonly found in fault zones, and miners working underground along a fault zone find themselves standing on the footwall, with the hanging wall over their heads.
If the hanging wall moves up or down during an earthquake, the fault is called a dip-slip fault (Figure 3-4). If the hanging wall moves sideways, parallel with the Earth’s surface, as shown in Figure 3-3, 3-5, and 3-6, the fault is called a strike-slip fault.
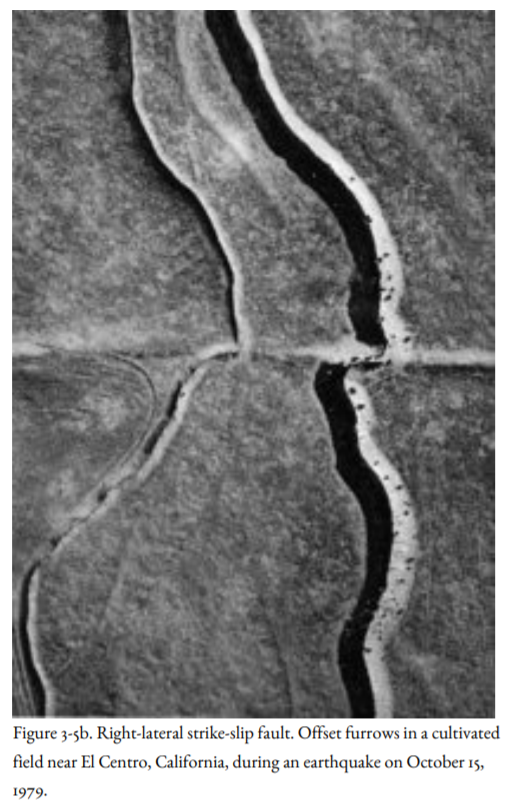
There are two kinds of strike-slip fault, right-lateral and left-lateral. If you stand on one side of a right-lateral fault, objects on the other side of the fault appear to move to your right during an earthquake (Figure 3-5a, b). The San Andreas Fault is the world’s best-known example of a right-lateral fault (Figure 3-5a). At a left-lateral fault, objects on the other side of the fault appear to move to your left (Figure 3-6). Some of the faults off the coast of Oregon and Washington are left-lateral faults (Figure 4-1, following chapter).


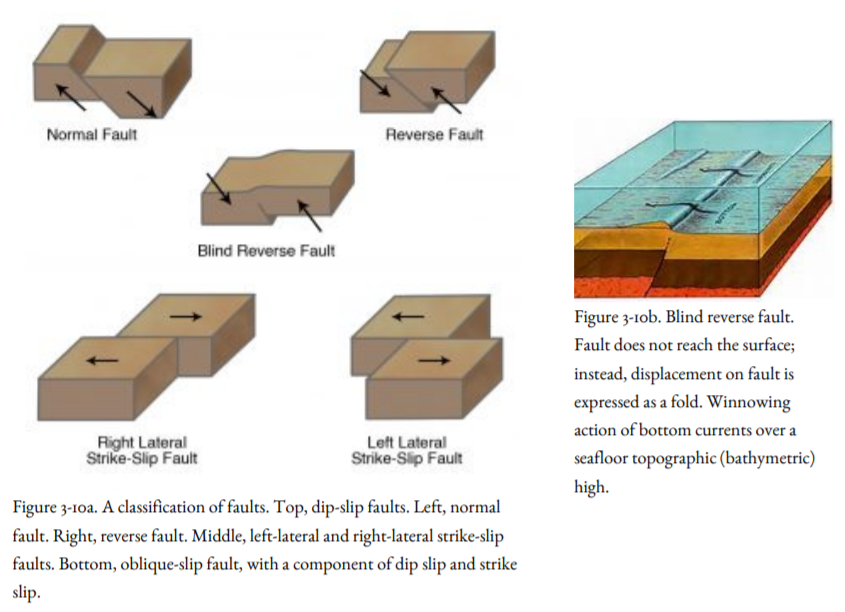
If the hanging wall of a dip-slip fault moves down with respect to the footwall, it is called a normal fault (Figure 3-7). This happens when the crust is being pulled apart, as in the case of faults bordering Steens Mountain in southeastern Oregon, or at sea-floor spreading centers. If the hanging wall moves up with respect to the footwall, it is called a reverse fault (Figure 3-8). This happens when the crust is jammed together. The Cascadia Subduction Zone, where the Juan de Fuca and Gorda oceanic plates are driving beneath the continent, is a very large-scale example of a reverse fault. The 1971 Sylmar Earthquake ruptured the San Fernando Reverse Fault, buckling sidewalks and raising the ground, as shown in Figure 3-8a. The 1999 Chi-Chi, Taiwan, Earthquake was accompanied by surface rupture on a reverse fault, including the rupture across a running track at a high school (Figure 3-8b). The Seattle Fault, extending east-west through downtown Seattle, is a reverse fault. Where the dip of a reverse fault is very low, it is called a thrust fault.


The 1983 Coalinga Earthquake in the central Coast Ranges and the 1994 Northridge Earthquake in the San Fernando Valley, both in California, were caused by rupture on reverse faults, but those faults did not reach the surface. Reverse faults that do not reach the surface are called blind faults, and if they have low dips, they are called blind thrusts. In many cases, such faults are expressed at the Earth’s surface as folds in rock. An upward fold in rock is called an anticline (Figure 3-9), and a downward fold is called a syncline. Before these two earthquakes, geologists thought that anticlines and synclines form slowly and gradually and are not related to earthquakes. Now it is known that they may hide blind faults that are the sources of earthquakes. Such folds cover blind faults in the linear ridges in the Yakima Valley of eastern Washington.

Figure 3-10a is a summary diagram showing the four types of faults that produce earthquakes: left-lateral strike-slip fault, right-lateral strike-slip fault, normal fault, and reverse fault. Figure 2-10b shows a blind reverse fault, the special type of reverse fault that does not reach the surface but is manifested at the surface as an anticline or a warp.