5.3.2: Elastic Rocks; How They Bend and Break
- Page ID
- 5917
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Overview

If you blow up a balloon, the addition of air causes the balloon to expand. If you then squeeze the balloon with your hands (Figure 3-1, left), the balloon will change its shape. Removing your hands causes the balloon to return to its former shape (Figure 3-1, left). If you take a thin board and bend it with your hands (Figure 3-1, right), the board will deform. If you let the board go, it will straighten out again. These are examples of the property of solids called elasticity. When air is blown into the balloon, or when the balloon is squeezed, or when the board is bent, strain energy is stored up inside the rubber walls of the balloon and within the board. When the balloon is released, or the board is let go, the strain energy is released as balloon and board return to their former shapes.
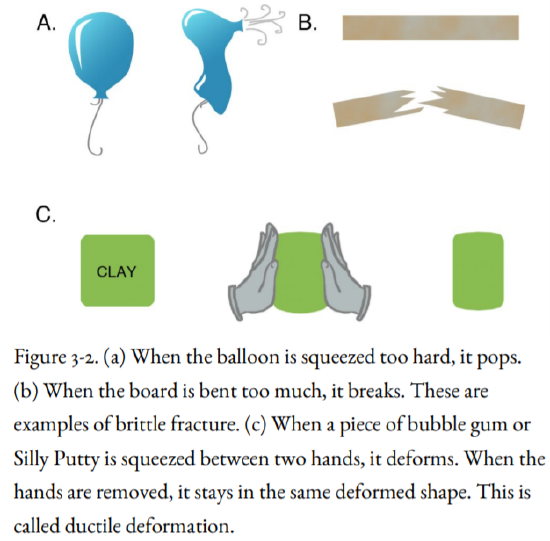
But if the balloon is blown up even further, it finally reaches a point where it can hold no more air, and it bursts (Figure 3-2, upper left). The strain energy is released in this case, too, but it is released abruptly, with a pop. Instead of returning to its former size, the balloon breaks into tattered fragments. In the same way, if the small board is bent too far, it breaks with a snap as the strain energy is released (Figure 3-2, upper right).
It is not so easy to picture rocks as being elastic, but they are. If a rock is squeezed in a laboratory rock press, it behaves like a rubber ball, changing its shape slightly. When the pressure of the rock press is released, the rock returns to its former shape, just as the balloon or the board does, as shown in Figure 3-1. But if the rock press continues to bear down on the rock with greater force, ultimately the rock will break, like the balloon or the board in Figure 3-2.
This elastic behavior is characteristic of most rocks in the brittle crust, shallower than the brittle-ductile transition, as shown in Figure 2-1. Rocks at greater depths commonly do not break by brittle fracture but deform like bubble gum or like the geologist’s favorite toy, Silly Putty. When a piece of Silly Putty is squeezed together, it deforms permanently; it does not return to its original shape after the squeezing hands are removed (Figure 3-2, bottom).
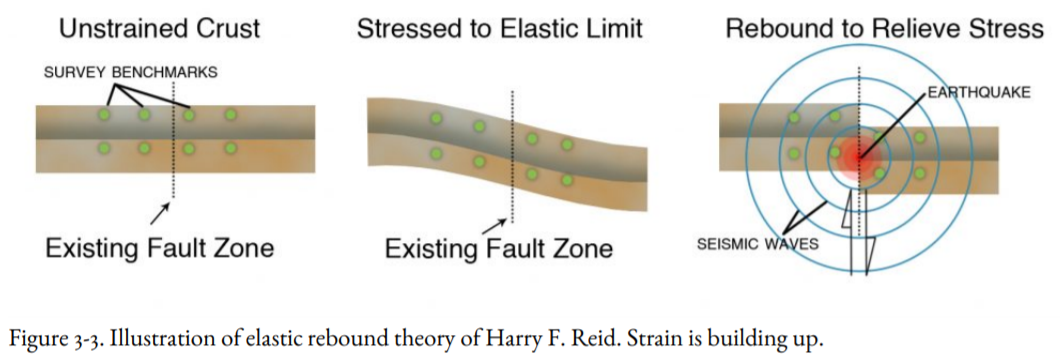

After the great San Francisco Earthquake of 1906 on the San Andreas Fault, Professor Harry F. Reid of Johns Hopkins University, a member of Andrew Lawson’s State Earthquake Investigation Commission, compared two nineteenth-century land surveys on both sides of the fault (Figure 3-3, left and center) with a new survey taken just after the earthquake (Figure 3-3, right). These survey comparisons showed that widely separated survey benchmarks on opposite sides of the fault had moved more than 10 feet (3.2 meters) with respect to each other even before the earthquake, and this slow movement was in the same direction as the sudden movement during the earthquake. Based on these observations, Reid proposed his elastic rebound theory, which states that the Earth’s crust acts like the bent board mentioned earlier. Strain accumulates in the crust until it causes the crust to rupture in an earthquake, like the breaking of the board and the bursting of the balloon.
Another half-century would pass before we would understand why the strain had built up in the brittle crust before the San Francisco Earthquake. We know now that it is due to plate tectonics. The Pacific Plate is slowly grinding past the North America Plate along the San Andreas Fault. But the San Andreas Fault, where the two plates are in contact, is stuck, and so the crust deforms elastically, like bending the board. The break is along the San Andreas Fault because it is relatively weak compared to other parts of the two plates that have not been broken repeatedly. A section of the fault that is slightly weaker than other sections gives way first, releasing the plate-tectonic strain as an earthquake.
If we knew the crustal strengths of various faults, and if we also knew the exact rate at which strain is building up in the crust at these faults, we could then forecast when the next earthquake would strike, an idea that occurred to Harry Reid. We are beginning to understand the rate at which strain builds up on a few of our most hazardous faults, like the San Andreas Fault. But we have very little confidence in our knowledge of the crustal strength that must be overcome to produce an earthquake. The crust is stronger in some places along the fault than others, and crustal strengths are probably different on the same part of a fault at different times in its history. This makes it difficult to forecast when the next earthquake will strike the San Andreas Fault, even though we know more about its earthquake history than any other fault on Earth.



