16.3: The Basic Idea Behind Climbing-Bed-Form Cross Stratification
- Page ID
- 4255
In general terms, the fundamental idea about cross stratification is easy to state (Figure \(\PageIndex{1}\)): as bed forms of one kind or other pass a given point on the bed, both the bed elevation and the local bed slope change with time. Consider a short time interval during the history of decrease and increase in bed elevation. After a temporary minimum in bed elevation is reached, deposition of new laminae takes place for a period of time, until a temporary maximum in bed elevation is reached. Then, as the bed elevation decreases again, there is complete or partial erosion of the newly deposited laminae and formation of a new truncation surface. After the next minimum in bed elevation, another set of laminae is deposited.

The preceding paragraph is still too general to give you a concrete idea about how moving bed forms generate cross stratification. Now I will be more specific. Take as an example a train of downstream-moving ripples in unidirectional flow. (The picture would be similar for dunes.) Each ripple moves slowly downstream, generally changing in size and shape as it moves. Sediment is stripped from the upstream (stoss) surface of each ripple and deposited on the downstream (lee) surface.
In your imagination, cut the train of ripples by a large number of vertical sections parallel to the mean flow direction (Figure \(\PageIndex{2}\)). The trough of a ripple is best defined by the curve formed by connecting all of the low points on these vertical sections where they cut the given trough (Figure \(\PageIndex{3}\)). This curve, which I will unofficially call the low-point curve, is generally sinuous in three dimensions. The low-point curve moves downstream with the ripples, and it changes its shape as it moves, like a writhing dragon, because trough depths and ripple speeds change with time.

As the low-point curve shifts downstream, it can be viewed as having the effect of a cheese-slicing wire: it seems to shave off the body of the ripple immediately downstream for removal by erosion, and in that way it prepares an undulating floor or surface for the deposition of advancing foresets by the ripple immediately upstream.
Depending on flow conditions and sediment size, the foreset laminae laid down by an advancing ripple vary widely in shape, from almost perfect planes sloping at the angle of repose, to sigmoidal curves that meet the surface of the trough downstream at a small angle (Figure \(\PageIndex{4}\)). Whatever their shape, these laminae are always deposited directly on the erosion surface that is formed, as just described above, by the downstream movement of the ripple trough into which the foresets prograde.

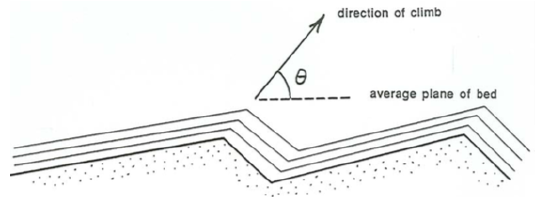
If no new sediment is added to the bed while the ripples move, the average bed elevation does not change with time, and the invisible plane that represents the average bed surface stays at the same elevation. On the average, the foresets deposited by a given ripple are entirely eroded away again as the next trough upstream passes by (Figure \(\PageIndex{5}\)). If new sediment is added everywhere to build the bed upward, however, the ripples no longer move parallel to the plane of the average bed surface but instead have a component of upward movement (Figure \(\PageIndex{6}\)). The resultant direction of ripple movement is described by the angle of climb, denoted by \(\theta\) in Figure \(\PageIndex{6}\). The tangent of \(\theta\) is equal to the average rate of bed aggradation divided by the ripple speed.

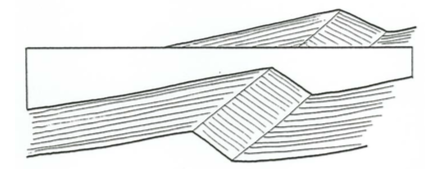
As the ripples climb in space, as described above, their troughs climb with them, so the erosion surface associated with the downstream movement of the low-point curve in a given trough passes above the erosion surface that was formed when the preceding trough passed by. The lowest parts of the foresets deposited by the ripple that was located between those two troughs are then preserved rather than eroded entirely (Figure \(\PageIndex{7}\)). This remnant set is bounded both above and below by erosion surfaces.

Figure \(\PageIndex{8}\) shows cross stratification in an ideally regular deposit produced by low-angle climb of a train of ripples. The heavy lines are erosion surfaces, and the light lines are foreset laminae. The profile of the ripple train as it existed at a given time is shown also. The upper parts of each ripple in the train, underneath the dashed part of the profile, were eliminated by later erosion. In real cross-stratified deposits of this kind, the erosion surfaces are irregularly sinuous because trough geometry changes with time, and the sets tend to pinch out both upstream and downstream because the ripples exist for only a finite distance of movement.

It is significant that what is most important in determining the geometry of this kind of cross-stratification is the geometry of the bed forms in the troughs, not near the crests. I should also point out that the height of the sets is always less than the height of the bed forms that were responsible for the cross stratification. If you compare the height of the cross sets with the height of the ripples in the dashed profile in Figure \(\PageIndex{8}\), you can see that for low angles of climb the set height is only a small fraction of the bed-form height.
The larger the angle of climb, the greater the fraction of foresets preserved. If the angle of climb of the ripples is greater than the slope angle of the stoss side of the ripples, then laminae are preserved on the stoss sides as well as on the lee sides, and the full profile of the ripple is preserved (Figure \(\PageIndex{9}\)). This happens when the rate of addition of new sediment to the bed is greater than the rate at which sediment is transported from the stoss side to the lee side of the ripple. The differences in geometry between Figure \(\PageIndex{8}\) and Figure \(\PageIndex{9}\) seem great, but keep in mind that the differences in environmental conditions are not large. The only difference is in the value of the angle of climb.
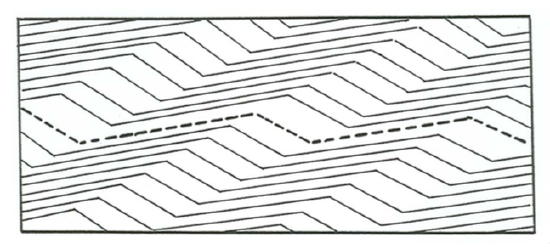
The lamination produced when ripples move with a positive angle of climb is called climbing-ripple cross stratification. Examples with angle of climb so small that the contacts between sets are erosional (as in Figure \(\PageIndex{8}\)) might be called erosional-stoss climbing-ripple cross stratification, and examples with angle of climb large enough for preservation of the full ripple profile (as in Figure \(\PageIndex{9}\)) might be called depositional-stoss climbing-ripple cross stratification.
Here is a recapitulation of some of the important points in this section. Cross stratification is formed by the erosion and deposition associated with a train of bed forms as the average bed elevation increases by net addition of sediment to some area of the bed. The angle of climb of the ripples depends on the ratio of rate of bed aggradation to speed of ripple movement. At high angles of climb, the entire ripple profile is preserved, and there are no erosion surfaces in the deposit. At low angles of climb, only the lower parts of foreset deposits are preserved, and the individual sets are bounded by erosion surfaces. The general nature of such stratification is common to moving bed forms of all sizes, from small current ripples to extremely large subaqueous or eolian dunes. Important differences in the details of stratification geometry arise from differences in bed-form geometry and how it changes with time.


