16.2: The Nature of Cross Stratification
- Page ID
- 4254
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cross stratification varies enormously in geometry. This is presumably a reflection of the great diversity of bed configurations produced by fluid flows over loose beds of sediment.
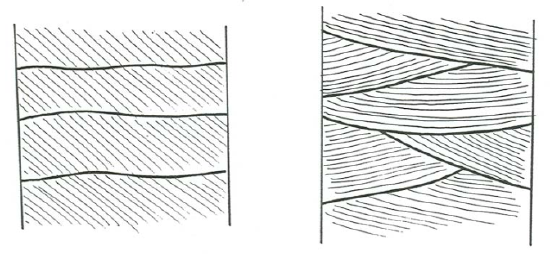
More commonly than not, cross-stratified deposits are arranged as packets or sets of conformable laminae, planar or curving, that are separated from adjacent sets by erosional set boundaries or truncation surfaces. The laminae within the sets may be planar or curving. Concave-up laminae are more common than convex-up laminae. (You will see why in the course of this chapter.) The orientations of the truncation surfaces are usually different from the orientations of the laminae within the sets. Commonly the lateral scale of the sets may be not much greater than the vertical scale, or it may be much greater. Figure \(\PageIndex{1}\) shows two common varieties of cross stratification as seen in sections normal to the overall plane of stratification. In some cases, there are no truncation surfaces within the cross-stratified deposit; Figure \(\PageIndex{2}\) shows a common example.

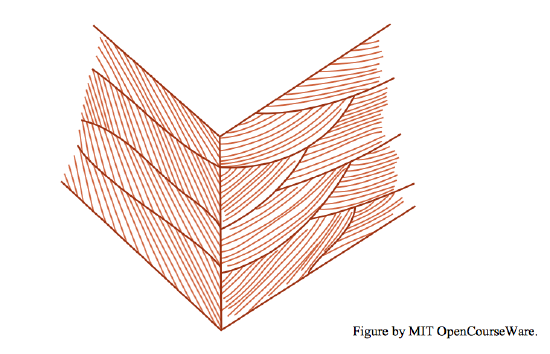
In a given local volume of cross-stratified deposit, the geometry of cross stratification commonly looks different in differently oriented sections normal to the overall plane of stratification. I will use the unofficial term anisotropic for such cross stratification. Figure \(\PageIndex{3}\) is a common example. Usually in such cases the cross laminae have a preferred direction of dip. (Note that the cross stratification on the two faces of the block shown in Figure \(\PageIndex{3}\) are the same as those used in Figure \(\PageIndex{1}\), which you might have thought were entirely unrelated.) If the geometry of cross stratification looks about the same in differently oriented sections, I will use the unofficial term isotropic.
Often a given cross-stratified bed may represent not just one depositional event but two or more separate depositional events, each one superimposed on the previous one. Such beds are said to be amalgamated. Sometimes it is easy to recognize the individual depositional events within the amalgamated bed; the stratification within each part of the bed can then be studied separately. But sometimes it is difficult to determine whether or not the bed is amalgamated.
Some General Points about Interpretation
In analogy with problems in geophysics, you might think in terms of the forward problem and the inverse problem. The forward problem in interpreting cross stratification that is generated by the movement of bed forms (arguably the most common kind) is that the flow generates moving bed forms, and the movement of the bed forms, together with a zero or nonzero rate of overall net aggradation of the bed, generates the stratification geometry (Figure \(\PageIndex{4}\)A). The inverse problem is more difficult (Figure \(\PageIndex{4}\)B): you start with the observed geometry of stratification and attempts to reconstruct the time history of bed geometry that generated that stratification. Then you attempt to reconstruct the flow conditions which were responsible for that time history of bed geometry.
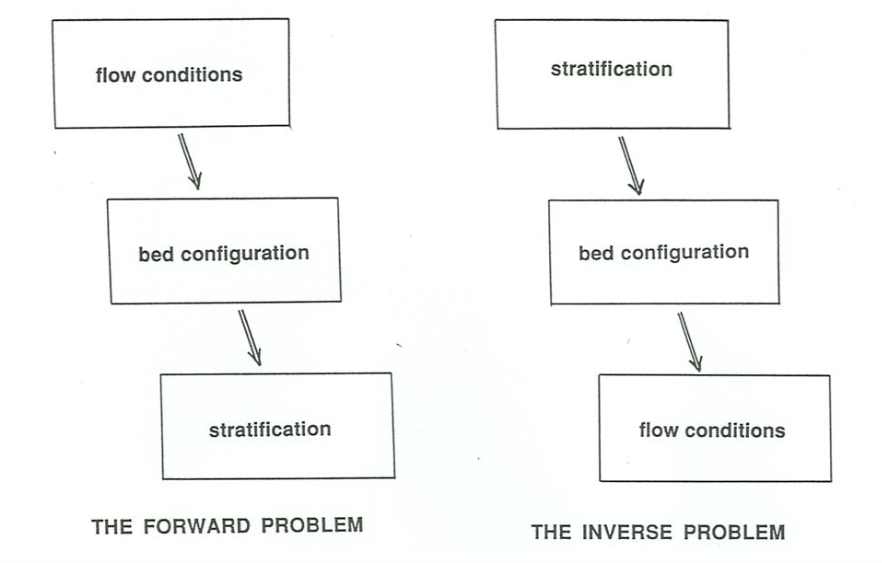
The difficulties in the inverse problem are that
- Nature does not give us time markers in the deposit, so information on time is lost in the generation of cross stratification, and
- In most cases some of the earlier-deposited sediment is eroded later as the cross stratification develops, so information on bed geometry is lost.
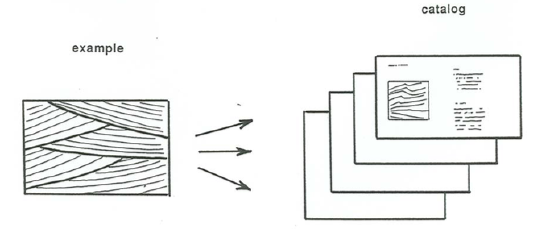
One way of circumventing the need to solve the difficult first step in the inverse problem (reconstructing the bed geometry from the stratification geometry) would be to have a complete catalog of the stratification geometries that are developed as a function of flow conditions and net aggradation rate (Figure \(\PageIndex{5}\)). One could then mindlessly compare the observed example of cross stratification with the patterns in the catalog to find the set of conditions that must have produced the observed example. There are two serious problems with this approach, though:
- We could never catalog all of the possible combinations of flow and aggradation rate; and
- Two or more rather different sets of conditions of flow and aggradation rate might produce very similar geometries of cross stratification.
When you are on the outcrop it is valuable to try to develop an idea of the bed configuration that was responsible for an observed cross-stratification geometry. That would be an incomplete task, however, even if you were able to carve the outcrop into thin slices to obtain a complete three-dimensional picture of the geometry. (Only in certain semi-lithified deposits can that actually be done without a lot of difficulty.) The best you can do is to obtain some partial ideas by examining the available faces of the outcrop. Those ideas are certain to be useful in developing an interpretation, but they are unlikely to give you anything near a complete picture of the cross-stratification geometry.
In actual practice, the sedimentologist on the outcrop relies upon certain widely accepted models for the development of cross stratification. (But keep in mind that not all cross stratification fits naturally into the available models.) Recall from the section on bed configurations that there are a small number of important bed phases (distinctive kinds of bed configuration), like unidirectional-flow ripples or dunes, or small two-dimensional oscillation ripples, or large three- dimensional oscillation ripples. Each of these bed phases is associated with some distinctive range of conditions of flow and particle size. Such a range of conditions is expressed graphically as the stability region a given bed phase occupies in some appropriate bed-phase graph.
The models are based on what is known empirically, by observations in flumes or natural flows, about the relationship between the bed phase and the cross stratification. The hope for the future is that, as our base of such observations increases, we can make more and more specific interpretations, but the fact remains that at the present time the interpretations can seldom be very specific. The need for careful laboratory and field studies of the stratification produced by definite combinations of flow conditions and net aggradation rate is still great.
The next section is a fairly detailed analysis of what is probably the most common and important kind of cross stratification: that produced by the movement of bed forms while the bed as a whole is undergoing net aggradation, slow or fast. Cross stratification of that kind is common in unidirectional flows of both water and air, and also in combined flows of water, and even in purely oscillatory flows of water, because, even in purely oscillatory flows, even slight asymmetry of the oscillation causes the bed forms to shift laterally at non-negligible rates. I will unofficially term cross stratification of this kind climbing-bed-forms cross stratification. Bed forms are said to climb when there is overall aggradation of the sediment bed while the bed forms are moving; see a later section for details.


