12.5: 2D Dunes and 3D Dunes
- Page ID
- 4229
It has become widely stated, in the literature on unidirectional-flow dunes, that at low flow strengths in the dune range the dunes tend to be straight- crested, with fairly even crest elevations and trough elevations. Such bed forms are referred to as two-dimensional (2D), in the accepted hydrodynamic sense that the geometry of the features can be represented by a single flow parallel cross section extending unchanged across the width of the flow. In contrast, at high flow strengths in the dune range the dunes show much greater crest curvature, much less crest continuity, and much greater variability in trough depths. Such bed forms are said to be three-dimensional (3D). Correspondingly, large-scale cross stratification produced by the movement of dunes is recognized as either two-dimensional, interpreted as representing relatively low flow strengths in the dune regime, or three-dimensional, interpreted as representing relatively high flow strengths—as you will see in Chapter 15. Recently, however, Venditti et al. (2005), on the basis of a systematic set of flume experiments using well sorted half-millimeter sand, claim that at low flow strengths in the dune regime initially 2D dunes eventually evolve into 3D dunes—a finding that is inconsistent with much of the earlier flume studies on dunes. The issue is not yet settled.
Dynamics of Unidirectional-Flow Bed Configurations
Introduction
How is it that a turbulent flow molds a bed of loose sediment into stable bed forms? The subject of bed-configuration dynamics has long been one of frustration and controversy. The fundamental difficulty is easy to state: it has to do with the difficulty of specifying adequately how sediment transport rate varies from place to place over a geometrically irregular transport surface. Before elaborating, I should make clear what I mean by the sediment transport rate at a point. I will address more fully in the following chapter the rate at which sediment is transported past a given cross section of the flow, in solids volume per unit width of the flow; it is usually denoted by \(q_{s}\). Here we need to think about how the “point” value of the volumetric transport rate, which you can view as the sediment transport rate over an arbitrarily small local area of the bed (again expressed per unit width of flow), varies from point to point on a nonplanar sediment bed. I will denote this by \(q_{s}\) also.
The velocity profile and the local bed shear stress (i.e., the skin friction) at some point on a nonplanar sediment bed, and their time variation, are not likely to be the same as at a point on a featureless planar bed with the same discharge and depth above it. This is because the details of forces and motions in accelerating and decelerating boundary layers are substantially different than in non-accelerating boundary layers. You have already seen this for the grossly non-uniform flows around bluff bodies like spheres and cylinders, but the effect is substantial even when much smaller accelerations or decelerations are caused by mild streamwise gradients in fluid pressure. The structure of the flow above any point tends to be inherited from upstream as the flow adjusts toward new conditions, so the flow at the given point depends in a complicated way on the shape of the bed for a long distance upstream. So even if \(q_{s}\) could be assumed to be in local equilibrium with the spatially varying flow, it could not be specified in any simple way as a function of position. Furthermore, \(q_{s}\) is likely not to be in equilibrium with local flow conditions, because a finite distance is needed for load to be dropped out or picked up as transport capacity changes. This distance should be expected to be greater for suspended load than for bed load, but it cannot be assumed to be negligible even for the latter.
The development of bed forms depends on the variation in \(q_{s}\) over the bed-form profile. In turn, \(q_{s}\) depends on the flow, and if an adequate expression for \(q_{s}\) as a function of position could be found it could be combined with the kinematic constraint imposed by conservation of sediment volume to give an equation that could be solved for the evolution of any initial bed geometry to a steady equilibrium geometry. But \(q_{s}\) cannot be specified so simply: as you have seen, the local sediment transport rate is itself a function of the bed configuration for which we are trying to solve.
In the face of this depressing prospect, many investigators have attempted with some limited success to glean physical understanding of the dynamics of bed configurations by making various simplifying assumptions that allow \(q_{s}\) to be expressed in a form that leads to mathematically tractable equations. Not many of these attempts have led to greatly improved understanding of the problem. This is a field of endeavor marked by an understandable scarcity of satisfying or useful results.
In this section I will concentrate not so much on a detailed review of the literature on bed-configuration dynamics as on the physical effects related to the existence, shape, size, and movement of bed forms. I will deal with each of these four aspects of dynamics in the following sections. The aim is to give you some appreciation of the potential and limitations of the various approaches to the problem of bed-configuration dynamics. It turns out to be easier to account qualitatively for shape and movement than for existence and size. As a necessary preliminary I will first derive the sediment conservation equation, a kinematic relation expressing conservation of sediment volume (or mass) that has to hold in any sediment-transporting system.
Sediment Conservation Equation
In any flow that transports sediment, the volume or mass of transported sediment must be conserved. This requirement leads to a purely kinematic relationship that has to hold irrespective of the dynamics of sediment transport. I will concentrate on a two-dimensional flow (one that varies in two dimensions only, downstream and upward from the bed but not in the cross- stream direction), but the principle is the same for a flow that varies in all three directions.
Consider a small rectangular region \(R\) of the sediment bed, with unit width normal to the flow and with length \(\Delta x\) in the flow direction (Figure \(\PageIndex{1}\)). The area of \(R\) is \(\Delta x\) because of the unit width. Denote by \(h\) the elevation of the bed above some arbitrary horizontal datum plane. Transport of sediment at any cross section can be expressed by \(q_{s}\), the volumetric sediment transport rate per unit width of flow; this may include sediment moving as bed load or in suspension. (In Chapter 12, the symbol \(q_{s}\) is used for the unit transport rate expressed as mass rather than as volume.) Let the depth-averaged volume concentration of the load be \(C\). (Strictly, \(C\) includes the concentration of bed load as well as suspended load.) The difference between \(q_{s}\) at the downstream boundary of \(R\), \((q_{s})_{out}\), and at the upstream boundary of \(R\), \((q_{s})_{in}\), is \(\Delta q_{s}\):
\[\left(q_{s}\right)_{o u t}-\left(q_{s}\right)_{i n}=\Delta q_{s} \label{12.32} \]
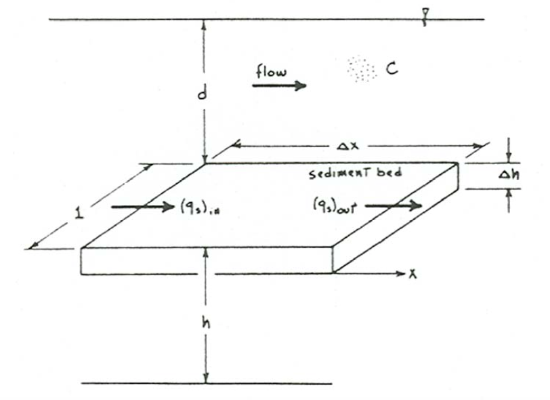
Any change \(\Delta h\) in bed elevation during some time interval \(\Delta t\) is caused by storage of sediment in \(R\) (deposition, or aggradation) or removal of sediment from \(R\) (erosion, or degradation). This change can be viewed as the sum of two contributions. One of these, \(\Delta h_{s}\), is caused by downstream change in \(q_{s}\): if \(q_{s}\) is greater across the upstream face than across the downstream face of \(R\), then sediment must be stored in \(R\), but if \(q_{s}\) is smaller, then sediment must be removed from storage in \(R\). The other contribution, \(\Delta h_{t}\), is caused by temporal change in \(C\): if the concentration of transported sediment is decreasing with time, then there must be deposition on all areas of the bed, but if the concentration is increasing, then there must be erosion (assuming that sediment is not being added to the flow from above). The bulk volume \(\Delta h_{s} \Delta x\) of aggraded or degraded bed in \(R\) due to downstream variation in \(q_{s}\) is equal to \(\Delta t\) times \((q_{s})_{in}-(q_{s})_{out}\), the rate of sediment storage due to the difference in transport rates across the upstream and downstream boundaries of \(R\), with a correction for the porosity effect (Equation 12.4.4):
\[h_{s} \Delta x=\Delta t\left[\left(q_{s}\right)_{i n}-\left(q_{s}\right)_{o u t}\right]=-K_{1} \Delta q_{s} \Delta t \label{12.33} \]
The porosity correction factor \(1/(1- \lambda)\), again denoted by \(K_{1}\), is needed because the volume of transported sediment is measured in solids volume whereas volume of bed sediment is measured in bulk volume, solids plus void space. The bulk volume of aggraded bed in \(R\) due to temporal variation in \(C\) is equal to minus the total change in volume of suspended sediment above \(R\), again corrected for the porosity effect:
\[\Delta h_{t} \Delta x=-K_{I} d \Delta C \Delta x \label{12.34} \]
where \(d\) is flow depth. Using Equations \ref{12.33} and \ref{12.34}, the average rate of change of bed elevation with time over \(R\), \(\Delta h/ \Delta t\), can now be written
\begin{align} \frac{\Delta h}{\Delta t} &=\frac{\Delta h_{S}}{\Delta t}+\frac{\Delta h_{t}}{\Delta t} \nonumber \\
&=-K_{1}\left(\frac{\Delta q_{s}}{\Delta x}+d \frac{\Delta C}{\Delta t}\right) \label{12.35} \end{align}
In the limit, as \(\Delta x \rightarrow 0\), Equation \ref{12.35} becomes
\[\frac{\Delta h}{\partial t}=-K_{I}\left(\frac{\partial q_{s}}{\partial x}+d \frac{\partial C}{\partial t}\right) \label{12.36} \]
The differential equation (Equation \ref{12.36}) is a volume-balance relationship that must hold at every point on the bed regardless of the sediment-transport dynamics. It relates the time rate of change of bed elevation at a point, \(\partial h/ \partial t\), to the downstream rate of change of sediment transport rate at that point, \(\partial q_{s} / \partial x\), and the time rate of change of total suspended-sediment concentration in the flow, \(\partial C/ \partial t\). It is usually called the sediment conservation equation, or the sediment continuity equation. Its use is essential in thinking about the temporal changes in bed geometry consequent upon spatial changes in transport rate. If \(C\) does not change with time, Equation \ref{12.36} becomes
\[\frac{\partial h}{\partial t}=-K_{1} \frac{\partial q_{s}}{\partial x} \label{12.37} \]
Rate of change of bed elevation is thus directly proportional to minus the downstream rate of change of sediment transport rate. If \(q_{s}\) decreases downstream for any reason, the bed is aggraded; if \(q_{s}\) increases downstream, the bed is degraded.
Movement of Bed Forms
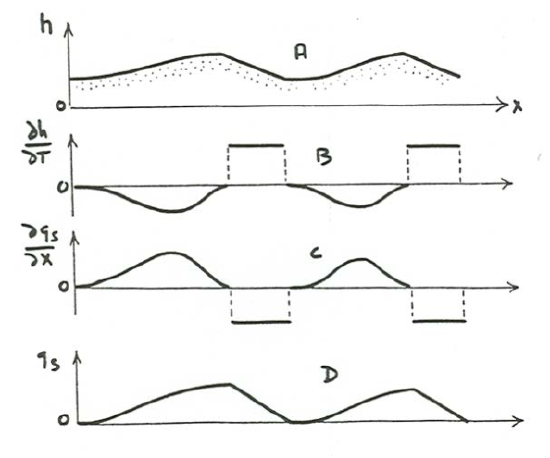
Armed with the sediment conservation equation and all that has been said about flow and sediment transport in turbulent boundary layers, what can we do about accounting for the existence, size, shape, and movement of loose-sediment bed forms? Look first at movement, because that is the most straightforward. Consider a hypothetical bed form like that in Figure \(\PageIndex{2}\)A, one element in a train of similar bed forms. Assume that the bed is in equilibrium with a steady sediment-transporting flow, and that the bed form moves downstream with unchanging size and shape. Equation \ref{12.37} associates with the movement of the bed form a particular pattern of variation of \(q_{s}\) over the bed-form profile in the following way. For the bed form to move downstream it is a kinematic necessity that \(\partial h/ \partial t\) be negative on the upstream side of the bed form and positive on the downstream side (Figure \(\PageIndex{2}\)B). Note that \(\partial h/ \partial t\) is zero at the crest and trough and has its greatest absolute value at points of steepest slope on the bed-form profile. By Equation \(\PageIndex{2}\), \(\partial q_{s}/ \partial x\) must vary with \(x\) in a sense just opposite to the variation in \(\partial h/ \partial t\) (Figure \(\PageIndex{2}\)C), and therefore \(q_{s}\) itself must be greatest at the bed-form crest and least in the trough (Figure \(\PageIndex{2}\)D). No zero point is shown on the \(q_{s}\) axis in Figure \(\PageIndex{2}\)D, because any position of the curve is consistent with that of the curve for \(\partial q_{s}/ \partial x\) in Figure \(\PageIndex{2}\)C. On ripple bed forms, \(q_{s}\) is zero or nearly so in the trough, and it may even be negative if the reverse flow in the separation zone is strong enough. Over antidunes, on the other hand, there may not be much relative variation in \(q_{s}\) over the bed-form profile. If the bed form is to move downstream \(q_{s}\) must increase up the stoss surface from the trough to the crest and must decrease down the lee surface from the crest to the next trough.
In any flow of a low-viscosity fluid like air or water with a velocity large enough to transport sediment, Reynolds numbers of flow over even small ridges or mounds on the bed are large enough for substantial front-to-back asymmetry in local bed shear stress. Recall that beginning at Reynolds numbers of about \(10\) the spacing of streamlines is closer, and therefore the skin friction is greater, on the front side of a cylinder or a sphere than on the back. This becomes more pronounced with increasing Reynolds number, and when flow separation eventually develops, the skin friction on the back is negligible. The effects are qualitatively the same for any ridge or mound on a sediment bed. So provided that the free surface remains approximately planar above the bed form, any bed form—even one whose height is only a few grain diameters—should have larger \(q_{s}\) on the upstream side than on the downstream side, with a maximum near the crest and a minimum somewhere in the trough. From Figure \(\PageIndex{2}\)D it is clear that this distribution of \(q_{s}\) guarantees downstream movement. This distribution of \(q_{s}\) is not likely to be exactly the one needed for maintenance of bed-form shape, but that is a matter for the next section; the bed form always moves downstream even if its shape tends to change at the same time.
If the mean-flow Froude number is close to one, surface gravity waves interact with the bed to produce stationary or slowly shifting bed waves that are in phase or almost in phase with the water-surface waves. For these upstream- shifting bed forms, which in an earlier section were called antidunes, the interaction of the free-surface wave and the bed-surface wave is such that \(q_{s}\) decreases up the upstream slope and increases down the downstream slope, resulting in upstream movement. No capsule statement can be made at this point that elucidates the dynamical reasons for this variation of \(q_{s}\).
Up to this point, it has been shown:
- what the variation in \(q_{s}\) has to be over a bed-form profile for the bed form to move, and
- that in the case of ripples the expected variations in \(q_{s}\) are in accord with the bed-form movement actually observed.
This may seem like a self-evident or trivial exercise, but it shows how we can obtain some insight into the behavior of bed forms by combining ideas about sediment transport with the sediment conservation equation, and it points the way toward other problems that are not as easy to deal with.
Shape of Bed Forms
Introduction
A striking characteristic of ripples and dunes is their asymmetrical profile, with a gently sloping upstream surface and a steeper, nearly angle-of-repose slip face on the downstream surface. Typically the bed profile shows a sharp angle at the top and bottom of the slip face—although reverse flow in the separation eddy can smooth out the slope break at the base. If the breaks in bed slope at the top and base of the slip face are ideally sharp, they represent jumps or discontinuities in \(\partial h/ \partial t\) and therefore by Equation \ref{12.37} in \(\partial q_{s}/ \partial x\) as well. Both \(h\) and \(q_{s}\) show kinks in their profiles at these points.
The Profile Shapes of Ripples and Dunes
In this section it is shown how the asymmetrical profile shape of ripples or dunes can be accounted for by combining the sediment conservation equation with a very general assumption about the physics of the sediment transport, namely that \(q_{s}\) increases with increasing flow strength. As in the preceding section, look at a hypothetical bed form in a train of identical bed forms (Figure \(\PageIndex{3}\)). In this section we start with a symmetrical bed form and consider how its profile changes with time. Consideration is resticted to flows with low Froude number, so that the water surface remains nearly planar whatever the bed geometry. The following line of reasoning was first presented by Exner (1925).
The strategy is to develop a relationship between bed elevation \(h\) and sediment transport rate \(q_{s}\), in order to put the sediment conservation equation into a form that can be solved for bed elevation as a function of position and time. As discussed above, ultimately we would like to be able to supply enough physics for this approach to lead to insights about how bed forms grow. For now we have to be content with very simple assumptions about \(q_{s}\) that will lead to understanding of bed-form shape but not bed-form growth.
The mathematically simplest assumption we can make about \(q_{s}\) is that it is directly proportional to some variable that describes the flow strength above the point at which \(q_{s}\) is measured. Using mean flow velocity \(U\) as this flow-strength variable,
\[q_{s} = K_{2}U \label{12.38} \]
where \(K_{2}\) is some constant. This has some serious shortcomings:
- there is a finite \(U\) for which \(q_{s}\) becomes nonzero, and at smaller \(U\) no sediment is moved;
- \(q_{s}\) does not vary linearly with \(U\) even when \(U\) is strong enough to move sediment; and
- if \(U\) rather than the skin friction is to be used to characterize \(q_{s}\), the flow depth \(d\) must also be specified in the function.
Notwithstanding these difficulties, this is a workable assumption for the task at hand, because it contains a large element of truth and it permits insight into how the bed evolves. More sophisticated assumptions would lead to the same qualitative results on the evolution of bed-form shape but would necessitate working with equations that are much more difficult to solve. Furthermore, the fact that even such an oversimplified assumption about qs accounts well for the evolution of bed-form shape is revealing in itself.
Using Equation \ref{12.38}, the sediment conservation equation (Equation \ref{12.37}) can be written
\[\frac {\partial h}{\partial t} = -K_{1}K_{2} \frac{\partial U}{\partial x} \label{12.39} \]
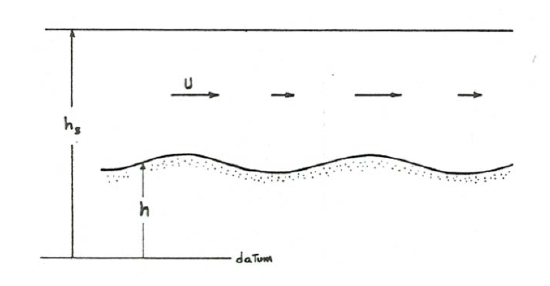
where \(K_{1}\) is again the porosity correction factor \(1/(1-\lambda)\). Conservation of fluid volume in the flow requires that, per unit width,
\[Ud = U(h_{s}-h) = K_{3} \label{12.40}\]
where \(h_{s}\) is water-surface elevation above the same arbitrary datum as for \(h\), and \(K_{3}\) is another constant. Equation \ref{12.40} tells you that where the flow is deeper over some two-dimensional bed configuration the velocity is smaller, and where the flow is shallower the velocity is greater, so by Equation \ref{12.36} there is deposition or erosion depending on the sign of \(\partial U / \partial x\). Combining Equations \ref{12.39} and \ref{12.40},
\[\frac {\partial h}{\partial t} = \frac {K_{1}K_{2}K_{3}}{(h_{s}-h)^{2}} \frac {\partial(h_{s}-h)}{\partial x} \label{12.41} \]
Assuming \(h_{s}\) to be constant (a reasonable assumption for flows at low Froude numbers) and writing \(K\) for the constant \(K_{1}K_{2}K_{3}\), Equation \ref{12.41} becomes
\[ \frac {\partial h}{\partial t} = \frac {K}{(h_{s}-h)^{2}} \frac {\partial h}{\partial x} \label{12.42} \]
You can verify for yourself that the solution to the fairly simple partial differential equation \ref{12.42} is
\[h_{s}-h = f \left[\frac {Kt}{(h_{s}-h)^{2}} - x \right] \label{12.43} \]
where \(f\) is an arbitrary function. To investigate the change in bed geometry with time, Exner (1925) assumed an initial bed topography given by a cosine function:
\[h = A_{o} + A_{1}\cos \frac{2\pi}{L}\left[x - \frac{K_{1}K_{2}t}{(h_{s}-h)^{2}} \right] \label{12.44} \]
where \(L\) is the spacing of the sinusoidal bed forms, and \(A_{o}\) and \(A_{1}\) are constants. This is what the bed profile at time \(t = 0\) would be if Equation \ref{12.43} is specialized in such a way that the bed profile as a function of \(x\) and \(t\) is
\[ h = A_{o} + A_{1}\cos \frac{2\pi}{L}\left[x - \frac{K_{1}K_{2}t}{(h_{s}-h)^{2}} \right] \label{12.45} \]
Figure \(\PageIndex{4}\) shows how the initial sinusoidal bed profile is modified with time according to Equation \ref{12.45}. The upstream slope of the bed form becomes gentler and the downstream slope becomes steeper, until finally the downstream slope passes through the vertical and an overhang develops. If this were a real bed form, a slip face would develop when the slope angle of the downstream side reaches the angle of repose. What is less clear from Figure \(\PageIndex{4}\) is that the bed form does not change in height as it changes in shape—but you can see from Equation \ref{12.45} that the highest point on the bed form always has a height \(h = A_{\text{o}} + A_{1}\), because the maximum value of the cosine function is one. This just means that the oversimplified assumption about \(q_{s}\) is inadequate to address the problem of bed-term growth.

So even a very simple assumption about the dependence of \(q_{s}\) on the flow accounts for the tendency for an originally symmetrical bed-form profile to evolve into the markedly asymmetrical profile characteristic of ripples. If we use a different function in Equations \ref{12.44} and \ref{12.45} to represent a different symmetrical or nearly symmetrical initial profile, the end result is just about the same. It is easy to observe just this kind of profile development in the laboratory: mold a long and low symmetrical ridge transverse to the flow on the sand bed of your flume, turn up the discharge until the sand moves, and then watch the profile as it is transformed gradually into a ripple, just as in Figure \(\PageIndex{4}\).
Growth of Bed Forms
Introduction
It is more difficult to account for the growth of bed forms than for their movement and shape. Here I will follow the same approach as before, that of combining sediment-transport dynamics with the sediment conservation equation, but it will not lead to results that are as satisfying. This is because bed-form growth and decay, or more generally the stability of bed configurations, depends on the interaction of flow and sediment transport in ways too complicated to be expressed or parameterized by local conditions like flow velocity, boundary shear stress, bed elevation, or bed slope: it involves the entire bed configuration, not just local variations in \(h\) and \(q_{s}\).
After describing a hypothetical flume experiment to examine some of the physical effects that have to be explained, I will again examine the qualitative kinematic constraints imposed on \(q_{s}\) during bed-form growth and then review some of the attempts that have been made to account for the existence of bed forms by deriving and solving equations for bed-form growth based on various assumptions about transport dynamics.
Hypothetical Flume Experiment
Make a long series of low transverse ridges on a sand bed in your flume (Figure \(\PageIndex{5}\)). It makes no difference whether these are initially symmetrical or asymmetrical, because you have already seen that the flow soon gives the profile of a transverse ridge a ripple shape, whatever its initial shape. It helps if you give the ridges an initial spacing that’s is not greatly different from what you know beforehand about equilibrium ripple spacing (if any) corresponding to the conditions of flow and sediment size you are going to use, because then you maximize the duration of your experiment by reducing the tendency for the bed forms to change their spacing by dividing and merging. If you make the train of initial ridges very regular, the ripples stay very much alike for a long time as they evolve. Eventually the inevitable irregularities in initial bed geometry (together with the stochastic nature of the grain transport itself) lead to the irregular geometry characteristic of real bed forms, but this irregularity is not essential to the existence of the bed forms. I emphasize that this experiment is a valid way of thinking about the physics of growth and decay of ripples within the context of the initial spacing you choose, although in general you cannot expect these ripples to be happy with the given spacing forever, even if at first they grow rather than decay.
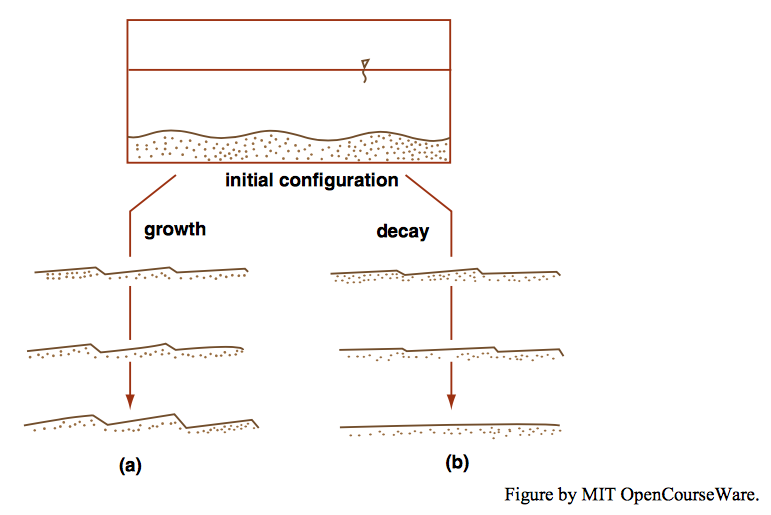
Pass a sand-moving current over the ridges, and keep track of the elevations of crests and troughs. Under some conditions (Figure \(\PageIndex{5}\)A) bed-form height increases as the troughs become deeper and the crests become higher. Stoss surfaces become steeper as well, because bed form spacing is strongly locked in to the original value and does not change, at least not until after a long running time. The lee surface is likely to become a slip face almost from the beginning, as you have already seen, and then stay that way. Associated with the increase in crest elevation and decrease in trough elevation is an increase in the volume of sand contained in the ripple per unit width (volume being measured upward from a plane coincident with the bed-form troughs). Time-lapse motion-picture photography of the ripples as they move is a good way of appreciating the changes in bed-form height and stoss-surface steepness. If you know something beforehand about equilibrium height of ripples as a function of flow conditions and sediment size, you could first generate a set of low ripples under one set of flow conditions and then change the flow conditions to what you know will make higher ripples, and then sit back and watch.
Now make a second run in which you start out with a train of initially high and steep ridges (Figure \(\PageIndex{5}\)B). The bed forms rapidly become asymmetrical as before, and sediment transport and ripple movement are qualitatively the same as before, but the bed forms are degraded as they move downstream: there is a gradual increase in trough elevation and decrease in crest elevation, and a corresponding gradual decrease in bed-form volume and also in the steepness of the stoss surface. Depending on sediment size and flow conditions, the ripples may stabilize at some equilibrium height, shape, and velocity, or they may become more and more like fast-moving sediment sheets with small downstream steps until ultimately the bed is transformed into a planar transport surface.
Both kinds of run are an approximate simulation of what happens when an equilibrium ripple bed configuration is subjected to a change in flow conditions. They leave out the effects of adjustment in ripple spacing by gradual accentuation of inevitable small irregularities in the profile and then division of one ripple into two, or fusion of two ripples into one. But they illustrate an important principle of bed-configuration stability: if very small disturbances grow larger, then some nonplanar bed configuration is the stable one under those conditions of flow and sediment, whereas if a preexisting nonplanar bed configuration is degraded to a planar transport surface, then upper-regime plane bed or lower-regime plane bed is the stable configuration. An analysis of how the ripple trains grow or decay in experiments like this should therefore provide insight into the dynamics of bed-form stability.
Conditions for Growth and Decay of Bed Forms
In this section I will reason as far as possible about the conditions for growth and decay of bed-form trains, like those in the hypothetical experiment described above. Take the \(x\) direction downstream and measure bed height from some plane parallel to the plane representing the mean bed surface and lying well below it. We will restrict ourselves to indefinitely long trains of two-dimensional flow-transverse bed forms in a transport system that’s uniform in the large, in the sense that \(q_{s}\) averaged over an entire bed form does not change in the downstream direction (Figure \(\PageIndex{6}\)).
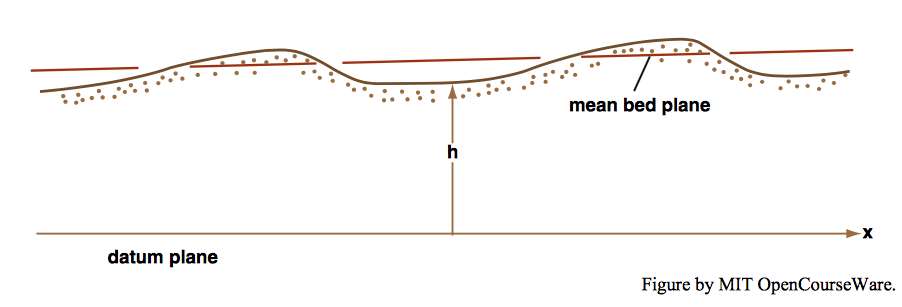
The bed-form profile may or may not be changing. In either case, \(\int h d x\) evaluated between two equivalent points on successive bed forms is constant. This expresses the condition that the bed is not aggrading or degrading on the average. If crests become higher, troughs have to become deeper in such a way that the mean bed elevation stays the same.
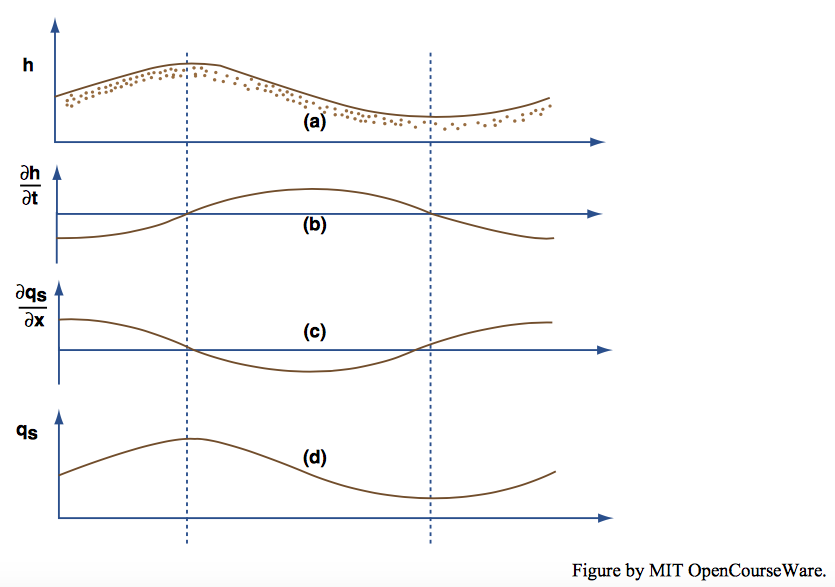
It is instructive to consider first the reference case of an unchanging profile. In the following, refer to Figure \(\PageIndex{7}\) (which is fundamentally the same as Figure \(\PageIndex{2}\)). The kinematic condition for an unchanging profile is that
\[h = f(x-U_{B}t) \label{12.46} \]
where \(U_{B}\) is a constant and \(f\) is some periodic function that represents the bed profile at a given time. The argument \(x-U_{B}t\) in the function implies that the profile propagates or shifts downstream at speed \(U_{B}\) as an unchanging wave form; \(U_{B}\) is therefore basically the same as the bed-form velocity used earlier in this chapter. To see the consequences of this condition, assume for now that the bed profile is a sine wave:
\[H = \sin (x-U_{B}t) \label{12.47} \]
There is really no loss of generality in doing this, because any periodic bed profile can be represented as a Fourier sum of sinusoidal components; at the end of this paragraph we will revert to a general periodic function \(f\).
Differentiating Equation \ref{12.47} with respect to \(t\),
\begin{align}
\frac{\partial h}{\partial t} &= \frac{\partial}{\partial t} \sin (x - U_{B}t) \nonumber \\
&= \frac{d[\sin(x-U_{B}t)]}{d(x-U_{B}t)} \frac{\partial(x-U_{B}t)}{\partial t} \nonumber \\
&=U_{B} \cos (x-U_{B}t) \label{12.48}
\end{align}
by use of the chain rule for partial differentiation. Note that \(\partial h/ \partial t\) in Equation \ref{12.48} is \(90^{\circ}\) out of phase with \(h\) in Equation \ref{12.46}, if the phase angle is measured in the downstream direction. In other words, the peak of the function in Equation \ref{12.48} is offset downstream from that of the function in Equation \ref{12.46} by one-quarter of a wavelength. (If you are not sure about the phase relationships, plot the four curves \(y = \cos x\), \(y = \sin x\), \(y = - \cos x\), and \(y = - \sin x\) and watch the sine wave shift along the \(x\) axis by \(90^{\circ}\), i.e., one-quarter of a wavelength, each time.) Now, to find \(\partial q_{s}/\partial x\) substitute Equation \ref{12.48} into the sediment conservation equation, Equation \ref{12.37}:
\begin{align} \frac {\partial q_{s}}{\partial x} &= - \frac {1}{K_{1}} \frac{\partial h}{\partial t} \nonumber \\
&= -\frac{U_{B}}{K_{1}}\cos (x-U_{B}t) \label{12.49} \end{align}
Note that \(\partial q_{s}/ \partial x\) in Equation \ref{12.49} is \(270^{\circ}\) out of phase with \(h\) in Equation \ref{12.46} because of the minus sign, i.e., the crest of the \(\partial q_{s}/ \partial x\) profile is one-quarter of a wavelength upstream of the crest of the bed-elevation profile. Integrating \( \partial q_{s}/ \partial x\) in Equation \ref{12.49} with respect to \(x\),
\begin{align}
q_{s}(x,t) &= \int \cos (x-U_{B}t)dx \nonumber
\\
&= \frac {U_{B}}{K_{1}} \int \cos(x-U_{B}t)dx \nonumber
\\
&= \frac{U_{B}}{K_{1}} \sin(x-U_{B}t) + c_{1}(t) \label{12.50}
\end{align}
where \(c_{1}(t)\) is a constant of integration that in general could be a function of \(t\), but is not in this case because we are assuming steady flow. (The constant of integration has to be a function of t because the integration is a “partial integration” of a function of two variables with respect to just one of those variables. while holding \(U_{B}t\) constant.) Note that \(q_{s}\) is in phase with the bed profile and differs only by a multiplicative constant \(U_{B}/K_{1}\) and an additive constant \(c_{1}\).
\[h(x,t) = f(x-ct) \label{12.51} \]
and,
\[q_{s}(x,t) = \frac{U_{B}}{K_{1}} f(x-U_{B}t) + c_{1} \label{12.52} \]
where \(c_{1}\) is just a constant that relates the average bed elevation to the average sediment transport rate. The variation of \(q_{s}\) is in phase with the bed profile and has the same shape except for the constant factor \(U_{B}/K_{1}\). Remember that this is all just a kinematic necessity; we have not specified anything about how \(q_{s}\) and \(h\) interact dynamically to produce the particular patterns observed.
From here on I will concentrate on lower-flow-regime ripple or dune bed forms. You have seen that if suspended-load transport is unimportant, lower-regime bed forms are dominated by slip faces that represent shock discontinuities. These discontinuities are associated with major flow separation over the bed form, but in a sense they are independent of the flow separation, in that they are a consequence of the steep increase in \(q_{s}\) with flow strength. Disregarding minor reverse flow in the lee eddy, \(q_{s}\) is zero from the toe of the slip face downstream to the reattachment point. If the profile is unchanging with time, this stretch of bed must be horizontal: within it \(q_{s}\) is independent of both \(x\) and \(t\) because it is identically zero there, so \(h\), which differs from \(q_{s}\) only by a multiplicative and an additive constant (compare Equations \ref{12.46} and \ref{12.50}), is constant in \(x\) and \(t\) there. This stretch of bed with \(q_{s} = 0\) may not be quite the lowest in the profile. because of some upchannel-directed sediment transport just upchannel of the reattachment zone, but it can safely be assumed so without affecting the conclusions of this section. Likewise, there is no dynamical requirement that the brink at the top of the slip face is the highest point on the profile, even if the profile is unchanging with time, but, because there is such a strong tendency for flow separation to develop upstream of a negatively sloping surface, the brink should be just about the highest point on the profile. It is therefore convenient to let the slip face represent the bed-form height \(H\), and it is also convenient to let the rate of downstream advance of the brink represent the velocity \(U_{B}\) of the ripple.
The presence of the shock discontinuity represented by the slip face imposes a further kinematic relationship that must hold among bed-form height, bed-form velocity, and the value of \(q_{s}\) at the brink:
\[(q_{s})_{brink} = K_{1}HU_{B} \label{12.53} \]
This is exactly the same as Equation \ref{12.31}; if you go back and review the derivation of that equation, you will see that it holds for the present situation as well, provided that all of the load is dumped at the break in slope at the brink to build the slip face forward. Equation \ref{12.53} holds generally, not just for an unchanging profile. Note that the slip-face angle drops out of the expression. This is consistent with the idea that the slip face is just the physical manifestation of a shock discontinuity in \(q_{s}\). The sediment delivered to the crest could just as well be falling off a cliff, in terms of the kinematics of the phenomenon!
In the light of all this bed-form kinematics, what can be done about accounting for the results of the hypothetical experiment? In the first run the bed forms started out too low and grew to some stable greater height, and they changed their shape in the process. After the bed forms reached equilibrium, the distributions of \(h\), \(\partial h/ \partial t\), \(\partial q_{s} / \partial x\), and \(q_{s}\) must have been as shown in Figure \(\PageIndex{8}\)B, which is qualitatively the same as Figure \(\PageIndex{2}\). Note the discontinuities in \(\partial h/ \partial t\) and \( \partial q_{s}/ \partial x\), reflecting the sharp kinks in bed elevation and transport rate at the top and bottom of the slip face. While the ripple train was adjusting, these curves must have been as shown in Figure \(\PageIndex{8}\)A. The differences between Figure \(\PageIndex{8}\)A and Figure \(\PageIndex{8}\)B look minor, but they are very significant for ripple growth. Large differences should not be expected anyway, because change in ripple shape and height is slow relative to ripple movement. The maximum in \(q_{s}\) on the stoss slope is located a little upstream of the brink rather than right at it. This leads to upward growth of the upper stoss surface during migration. Also, there is a downchannel slope to the bed between the base of the slip face and the low point on the profile. These two differences reflect stronger-than-equilibrium scour in the reattachment zone and just downstream, leading to a temporal lowering of bed elevation in the trough. The extra sediment produced by this scour is transported up the stoss surface to steepen the upper part. The slip face lengthens as it builds into the deepening trough, making ripple height greater. By Equation \ref{12.53}, \(U_{B}\) tends to decrease as the slip face lengthens, and this augments the tendency for increased trough scour, because the reattachment zone passes more slowly along the bed in the trough as it is driven downstream by the next ripple coming along. Eventually the geometry and sediment transport adjust to the new flow, and a picture qualitatively like that of Figure \(\PageIndex{8}\)B is reestablished with a greater ripple height and a different ripple shape.
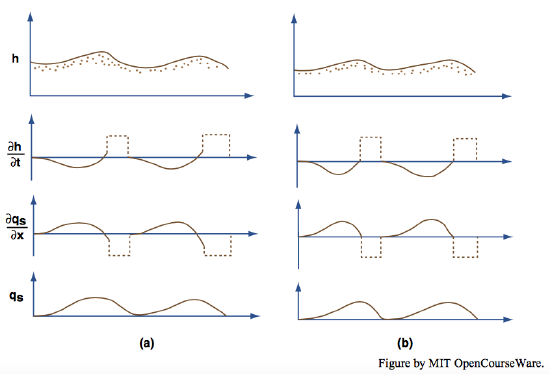
In the second run, the bed forms started out too large and shrank either to some stable smaller height or were degraded completely. Figure \(\PageIndex{9}\) shows the distributions of \(h\), \(\partial h/ \partial t\), \(\partial q_{s}/ \partial x\), and \(q_{s}\) as the ripples were changing. If the ripples reached equilibrium in the run, Figure \(\PageIndex{9}\)A can be compared with Figure \(\PageIndex{9}\)B for the stable smaller ripples. If not, then Figure \(\PageIndex{9}\)A evolves into an uninteresting graph, not shown, in which \(h\) and \(q_{s}\) are positive and constant, and \(\partial h/\partial t\) and \(\partial q_{s}/\parital x\) are zero. Note in Figure \(\PageIndex{9}\)A that \(q_{s}\) is increasing at all points up the stoss surface from reattachment. Because \(\partial q_{s}/\partial x\) is still positive at the brink, \(\partial h/\partial t\) is negative there, so the crest elevation is decreasing with time. Scour in the trough is weaker than needed to maintain trough depth, so the bed slopes upward at all points downchannel of the base of the slip face, although no sediment is moved on the stretch of bed from there to the reattachment point. Trough elevation increases as the slip face becomes shorter by building onto the upsloping trough surface, so both ripple height and ripple volume decrease. By Equation \ref{12.53}, \(U_{B}\) tends to increase as the slip face becomes shorter, and this augments the weakening of scour in the trough because it causes the reattachment zone to sweep more rapidly downchannel.
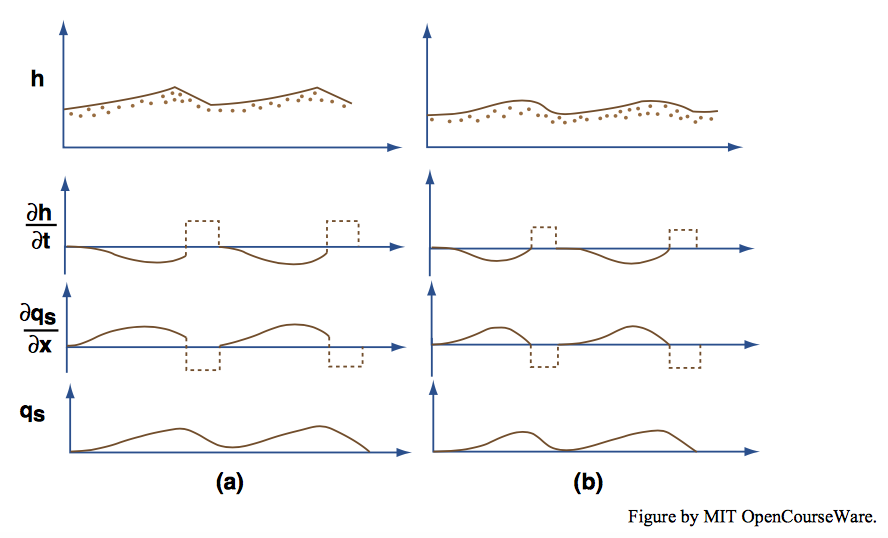
In summary, changes in ripple height, shape, and velocity can be viewed in terms of the interaction among three related but distinguishable factors:
- The dependence of \(q_{s}\) on flow structure along the reach of bed extending from the reattachment point up the stoss surface to the brink;
- The rate at which the zones of differing flow structure downstream of the point of flow separation are swept along the bed surface by the advancing crest upstream, as specified by the relation expressed by Equation \ref{12.53} among slip-face height, ripple velocity, and sediment transport rate at the brink; and
- The slope of the trough surface onto which the slip face builds.
We have not solved any problems of bed-form stability here; we have only shown what factors are involved. Nonetheless, this line of approach is nonetheless useful, in that it aids in an understanding of the problem.
Stability Analyses
In order to understand the existence of bed forms, various investigators have resorted to stability analysis, a mathematical technique, useful in many areas of applied mathematics, whereby a partial differential equation is somehow developed that gives the rate of growth of a periodic disturbance or perturbation introduced onto the bed surface. The assumption is that if the rate of growth of the perturbation is positive the perturbation is amplified with time, and bed forms eventually develop. If, on the other hand, the perturbation is damped, then a plane bed should be the only stable bed configuration. The differential equation is of the same kind as used in the preceding sections. It comes about by supplying a relationship for \(q_{s}\) as a function of flow, which can be used to put the sediment conservation equation into a solvable form. This equation has to go beyond the oversimplified assumptions made in the section on shape of ripples, because we saw that those assumptions account only for change in ripple shape, not in ripple volume.
The great advantage of the stability approach is that it can be developed for perturbations with amplitude very small compared to wavelength, so that bed slopes are very small. It is then more likely that relationships for sediment transport that are not grossly unrealistic can be specified. By the same token, however, without further analysis this approach gives no information on the nature of the resulting bed configuration when the perturbation is amplified to the extent that that the small-amplitude assumption is no longer valid. There is the possibility, however, that an estimate of the spacing of the resulting bed forms can be obtained by determining the wavelength of the perturbation that shows the fastest rate of growth.
It is worth mentioning several attempts, along the above lines to account for observed bed configurations: those by Kennedy (1963, 1969), Smith (1970), Engelund (1970; see also Engelund and Fredsøe, 1974), Richards (1980), McLean (1990), Ji and Mendoza (1997), and Jerolmack et al. (2006). (You can see, from that list, that the pursuit of the fundamental dynamics by means of stability analysis has had a long history. The last word has not been spoken on that topic—a manifestation of the enduring obstacles to a unified and generally accepted theory.)
Kennedy’s analysis, which is most relevant to bed configurations at mean-flow Froude numbers close to one, assumes inviscid flow with a wavy free surface over a wavy boundary. By making simple assumptions about sediment transport rate as a function of near-bed velocity, Kennedy developed a framework that accounts well for the occurrence of antidunes—bed forms whose behavior is dependent upon the presence of the free surface. The theory does not so much predict the bed configuration as provide a rational framework in which to account for it: as do many later analyses by others, the analysis involves a parameter called the lag distance (the distance by which local sediment transport rate lags behind the local velocity at the bed) that would have to be supplied by either experiment or additional theory. For the stability of antidunes, the theory works well with physically realistic assumptions about the lag distance in that it succeeds in accounting for the observed spacing of antidunes. As might be expected from the essential role of the presence of the wavy free surface in the analysis, the theory is less successful in accounting for dunes. Kennedy’s work stimulated many subsequent attempts along the same lines.
Smith (1970) developed a stability analysis to deal specifically with flow at Froude numbers low enough that free-surface effects are negligible. Making suitable assumptions about nature of the flow (eddy-viscous flow of real fluid) and about sediment transport rate as a function of flow, Smith developed an equation that, when linearized by retaining only the most significant terms, is amenable to stability analysis. The result is that, for these not grossly unrealistic assumptions about flow and sediment transport, a positive growth rate, and therefore development of ripple-like bed configurations, is predicted for all flows strong enough to transport sediment. This is a rather fundamental and satisfying way to account for the existence of ripple-like bed configurations under reasonably realistic assumptions about flow and sediment transport. Even aside from the usual problem of not being able to take finite-amplitude effects into account without further theory, however, the analysis does not account for the existence of plane-bed stability at the higher flow strengths.
Engelund (1970; see also Fredsøe, 1974, and Engelund and Fredsøe, 1974), in a somewhat different approach also involving an eddy-viscous fluid, but taking account of the distinction between suspended-load transport and bed-load transport, was able to account well for the transition from dunes to plane bed as a function of both grain size and flow strength. Richards (1980), using a more realistic description of the structure of turbulence near the bed, was able to account for the separate existence of ripples and dunes by predicting the occurrence of two separate modes of instability, one (for ripples) dependent on the bed roughness and the other (for dunes) dependent on the flow depth. More recently, McLean (1990) and Li and Mendoza (1997) have gone beyond linear stability analysis to account also for nonlinear finite-amplitude effects. Even more recently, Jerolmack et al. (2006) have developed a model of bed-form development that unifies the dynamics of ripples and dunes.
Are Ripples and Dunes Different?
Of course, the answer is “yes”: dunes are larger than ripples. I should rephrase the question: Are the dynamics of ripples and dunes different? Most investigators have assumed that the answer to that question is also “yes”. Those who have attempted to account for the existence of ripples and dunes by means of a stability analysis (see the preceding section) have invoked a short-wavelength instability that leads to the development of ripples and a long-wavelength instability that leads to the development of dunes. In that approach, the key to the development of ripples is a spatial (downstream) lag between bed shear stress and sediment transport rate (that is, the sedimentary transport rate lags the bed shear stress) in the case of ripples, and a spatial lag between bed shear stress that also involves suspended-load transport, in the case of dunes.
It has commonly been believed that there is a gap in spacing between what are considered to be ripples and what are considered to be dunes. In reporting a consensus among the “experts”, Ashley (1990) chose a cutoff of \(0.6\) \(\mathrm{m}\) spacing for the boundary between ripples and dunes. There indeed seems to be a paucity of bed forms with spacings in the range between a few decimeters and one meter (Figure \(\PageIndex{10}\)).
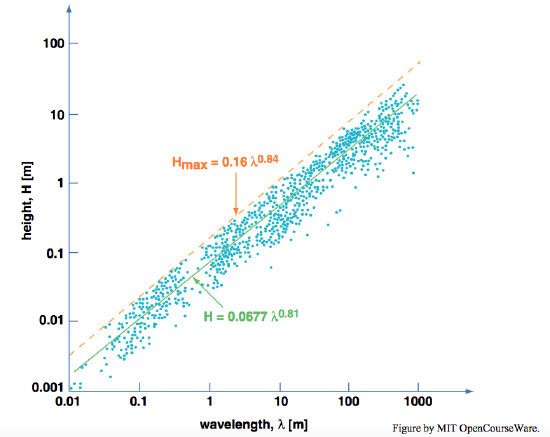
Clearly there is not a complete absence of ripple or dune bed forms in that range—but it is still uncertain whether there is a continuum in spacing between undoubted ripples and undoubted dunes, or whether those intermediate cases are stunted dunes (in very shallow flow) or newly developing dunes. The matter has not yet reached the stage of a general consensus. There have been only a few studies aimed particularly at describing the transition between ripples and dunes (Boguchwal and Southard, 1990; Bennett and Best, 1996; Lopez et al., 2000; Robert and Uhlman, 2001). The range of mean flow velocity, for a given flow depth, over which the transition is completed is rather narrow. Within that narrow range, there is a large change in bed-form geometry as well as the associated flow characteristics. What all of these studies seem to agree upon is that there is a real dynamical distinction between ripples and dunes.


