7.7: Planetary Boundary Layers- The Ekman Layer, The Logarithmic Layer, and The Mixed Layer
- Page ID
- 4894
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
I am now going to subject you to a further set of flow layers, one of which, the Ekman layer, you have already encountered. You can think of this concluding section as a continuation of the material on boundary layers in Chapter 4, in the context of the large-scale bottom boundary layers in the atmosphere and in the oceans—which are called planetary boundary layers. (Note on terminology: in the atmosphere, it is called the atmospheric boundary layer; in flow in the shallow ocean, on continental shelves, for example, it is often called the bottom boundary layer; in the deep ocean, it is commonly called the benthic boundary layer. They are all the same, in essential dynamics).
Given that the winds and the ocean bottom currents flow over a solid boundary, it is understandable that there must be a bottom boundary layer in those settings. All of what was said about boundary layers in Chapter 4 can be applied to these planetary boundary layers—but with the important additional effect of the Earth’s rotation. In the previous section you learned about the Ekman layer, which, as a part of the planetary boundary layer, is an additional boundary-layer element brought about by the Coriolis effect.
The Mixed Layer
Stable stratification is ubiquitous in the atmosphere and the oceans. By stable stratification I mean that the vertical profile of fluid density in the medium is such that if you were to capture a small parcel of the fluid and move it bodily upward, without allowing any exchange of thermal energy between the parcel and its surroundings (in thermodynamics that is called an adiabatic process), it would arrive with density greater than its surroundings, and if you moved it downward, it would arrive with density less than its surroundings. That means that there is no tendency for convective vertical mixing: the density stratification is such that the parcel would always be pushed back toward the place where it started.
The atmosphere and the oceans are fundamentally different in respect to the origin of stable stratification. The main reason is that the atmosphere is heated at its base: the sun warms the ground surface, and the lowermost layer of the atmosphere is in turn warmed by the ground—during the day, that is, and not at all times and places even then. By contrast, the heating of the lowermost layer of the ocean by heat flow from the substrate is not very important in the dynamics of near-bottom flow.
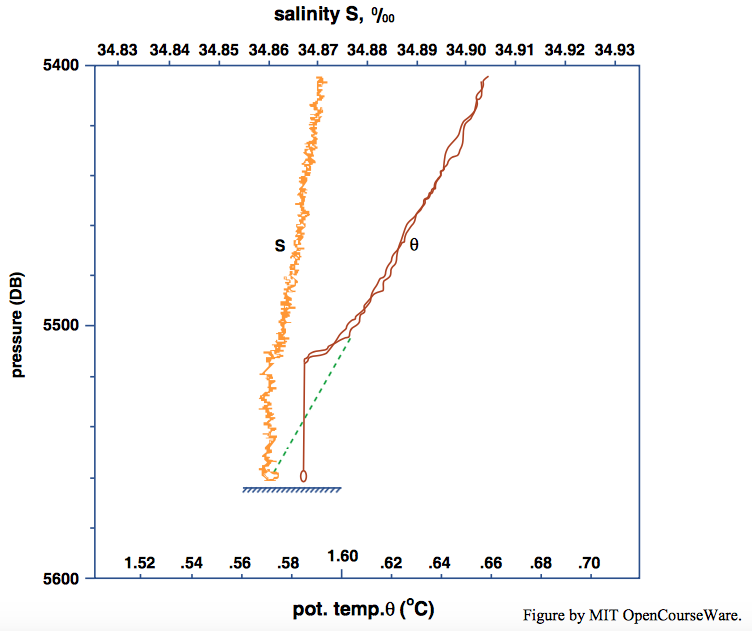
You learned back in Chapters 3 and 4 that shear produces turbulence, and the stronger the shearing, the more likely it is that turbulence is produced. You also learned that, in flow of a viscous fluid past a boundary, the shear is strongest near the boundary and decreases way from the boundary. Here you need to think in terms of a competition: one the one hand, stratification tends to damp turbulence, whereas on the other hand, shear tends to produce turbulence. That leads to the concept that under the right conditions a turbulent layer develops adjacent to the boundary, in which turbulence produced by shear causes vertical mixing, as you learned about in Chapter 4. Such a layer is called the mixed layer. So the thickness of the mixed layer depends upon the competition between the intensity of the near-boundary shear and the strength of the stratification. Figure \(\PageIndex{1}\) shows a striking example of a mixed layer in the ocean.
Things are different in the atmosphere, because of the tendency for diurnal (day to night) difference in heating of the ground by solar radiation during the day and cooling of the ground by long-wave radiation to space during the night. The tendency for development of a mixed layer by shear turbulence is present in the atmosphere as well as the ocean, but the other effect, strong convection by ground heating, is even more important. The two processes act together to produce a well-defined mixed layer, even when the atmosphere is overall stably stratified (as is true most of the time, except in the vicinity of low- pressure areas, where uprise of air through a deep layer is caused by other effects). At times when the convectively uprising air reaches the local condensation level, puffy cumulus clouds form, and mark the top of the mixed layer nicely. You probably have experienced the structure of the atmospheric mixed layer yourself: as you gain altitude in your jetliner on a nice sunny day, the ride is bumpy until you reach the tops of the cumulus clouds, whereafter you have a much smoother ride.
What is the relationship between the mixed layer, on the one hand, and the Ekman layer, which you learned about earlier in this chapter, on the other hand? Commonly, the thickness of the mixed layer in the ocean is the greater part of a hundred meters, and that of the mixed layer in the atmosphere is on the order of a thousand meters. That’s several times the thickness of the Ekman layer. So you can think of the Ekman layer as typically being embedded deeply in the mixed layer. The flow is turbulent at heights above the bottom well above the turning of the flow velocity in the Ekman layer.
A grand large-scale mental experiment might not be out of place here. Suppose that you could somehow set up a gigantic tank, as large as an ocean basin, on a rotating platform. To a depth of a few thousands of meters, fill the tank with water that is at the same temperature (and salinity) throughout, so that there is no density stratification whatsoever. Somehow, produce a broad current in the medium, on a scale of thousands of kilometers on both the along-flow and cross-flow directions. In the parlance of geophysical fluid dynamics, what we are aiming for is a flow with a very small Rossby number.
What would you observe? A vertical profile of velocity that is the same, in essential respects, as the fully developed boundary-layer flow, akin to what is shown in Figure 3.6.5, back in Chapter 3 on boundary layers. The boundary layer would have grown to occupy the full depth of the flow, and the flow would be turbulent throughout. The Ekman layer, however, would be there, immediately above the bottom: that’s the fundamental difference between a deep uniform flow in a nonrotating system and one in a rotating system. The fundamental reason why such a flow is never observed in the deep ocean is the ubiquitous stable stratification, described above: the thickness of the turbulent boundary-layer flow is severely limited by that stratification.
The Logarithmic Layer
You might be wondering, at this point, about the relevance of the large body of material on flow resistance and velocity profiles in turbulent shear flows past a solid boundary, treated in much detail in Chapter 4, to planetary boundary-layer flow. The essential point is easy to state: everything developed in Chapter 4 is relevant to the planetary boundary layer. Very near the bottom boundary, deep in the mixed layer (and at the base of the Ekman layer) the same arguments used in Chapter 4 to deal with the inner layer and the outer layer of the flow hold equally well in the case of the planetary boundary layer: there may or may not be a viscous sublayer, depending upon the particular the value of the boundary Reynolds number, but in any case there is a part of the inner layer that is described by the law of the wall. Also, there is an outer layer, where a “velocity defect law” must hold, and there is an overlap layer, which (as mentioned in Chapter 4 but not developed in detail) requires that both the law of the wall and the velocity defect law be logarithmic. In the context of the planetary boundary layer, this lowermost layer, in which the velocity profile is logarithmic, is called the logarithmic layer. In the ocean, the logarithmic layer is typically only few meters thick—but it is what the bottom sediment feels! It is thicker in the atmosphere, but still not nearly as thick as the entire Ekman layer.
References Cited for Chapter 7
Armi, L., and Millard, R.C., Jr., 1976, The bottom boundary layer of the deep ocean: Journal of Physical Oceanography, v. 81, p. 4983-4990.
Gross, M.G., 19090, Oceanography; A View of the Earth, Fifth Edition: Englewood Cliffs, New Jersey, Prentice-Hall, 441 p.
Gustafson, T., and Kullenberg, B., 1933, Trägheitsströmungen in deer Ostsee: Medd. Göteborgs Oceanogr. Inst., no. 5.
Neumann, G, and Pierson, W..J., Jr., 1966, Principles of Physical Oceanography: Englewood Cliffs, New Jersey, Prentice-Hall, 545 p.
Pedlosky, J, 1987, Geophysical Fluid Dynamics, 2nd Edition: New York, Springer-Verlag.


