5.7: Gradually Varied Flow
- Page ID
- 4868
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Nonuniform flows for which the changes in depth and velocity are so abrupt that radial accelerations distort the vertical distribution of fluid pressure from the hydrostatic condition are called rapidly varied flows. Flow over a sharp-crested dam or weir, and flow under a sluice gate, are good examples. Such flows are difficult to deal with analytically, and I will not pursue them here, although they are important in many engineering applications.
Nonuniform open-channel flows for which the changes in depth and velocity are slow enough in the downstream direction that the vertical distribution of fluid pressure from the free surface to the bottom is not much different from hydrostatic are called gradually varied flows. An example is the flow transition over a gentle step, introduced at the beginning of this chapter (Fig. 5.2.1). It is completed in a sufficiently short distance that loss of flow energy by friction can be neglected, but the fluid accelerations are still sufficiently small that the vertical distribution of fluid pressure is close to being hydrostatic. In most gradually varied flows, however, the change takes place over a distance sufficiently great that we cannot assume zero energy loss due to bottom friction. The second channel-transition example posed at the beginning of this chapter falls into that category.
To see what happens to the elevation of the water surface through a transition over such a long distance that bottom friction cannot be neglected, we need to start with the equation for the total head at a cross section of the flow and differentiate each term with respect to distance in the flow direction. (In what follows, I am going to write \(\gamma\) instead of \(d\) for the flow depth.) Start with Equation 5.4.1, written using the elevation of the channel bottom \(h_{\text{o}}\) (cf. Equation 5.4.2):
\[E_{w}=\frac{U^{2}}{2 g}+y+h_{o} \label{5.22}\]
Differentiate Equation 5.5.1 with respect to the flow direction \(x\):
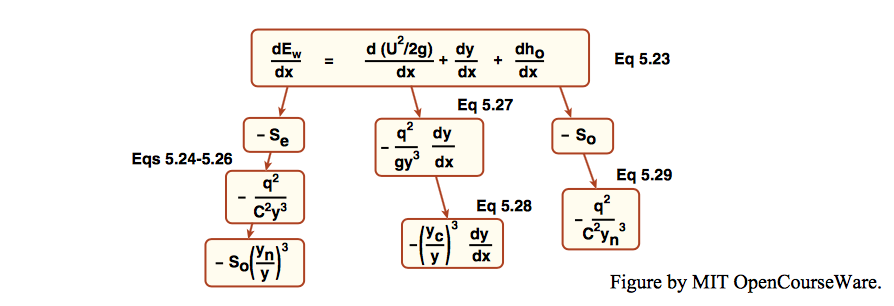
\[\frac{d E_{w}}{d x}=\frac{\mathrm{d}\left(U^{2} / 2 g\right)}{d x}+\frac{d y}{d x}+\frac{d h_{o}}{d x} \label{5.23} \]
The term on the left side of Equation \ref{5.23} is the rate of change in total energy in the downstream direction. This is always negative, because energy is inevitably lost by friction. Think in terms of the downward slope of the line formed by plotting \(E_{w}\) as a function of downstream distance. This slope, denoted by \(S_{e}\), is what was called the energy slope, or the energy gradient, or the slope of the energy line earlier in this chapter. By convention, such a negative slope is considered to be positive \(S_{e}\), so we replace \(d E_{w} / d x\) in Equation \ref{5.23} by \(-S_{e}\).
Friction loss in nonuniform flow is not well studied, but to get somewhere just in a qualitative way we can assume that the friction loss in slightly to moderately nonuniform flow is not greatly different from what it would be in uniform flow—and we have already dealt with that satisfactorily in Chapter 4. Remember the Chézy coefficient I introduced back then? According to Equation 4.6.3, repeated here as Equation \ref{5.24},
\[U=C(y \sin \alpha)^{1 / 2} \label{5.24} \]
Assuming that \(\tan \alpha \approx \sin \alpha\), which is a very good approximation for the small angles we are dealing with here, and keeping in mind that the slope \(\tan \alpha\) is just \(S_{e}\), and solving for \(S_{e}\),
\[S_{e}=\frac{U^{2}}{C^{2} y} \label{5.25} \]
This can be written a little more usefully by getting rid of \(U\) by use of the relation \(q = Uy\); remember that the discharge per unit channel width \(q\) (which is constant along the channel) is related to the mean velocity \(U\) by this relation. Then Equation \ref{5.25} can be written
\[S_{e}=\frac{q^{2}}{C^{2} y^{3}} \label{5.26} \]
Now for some manipulation of the right side of Equation \ref{5.23}. The first term on the right can be massaged in the following way to put it into a more useful form. In what follows, again keep in mind that the discharge per unit channel width \(q\) is related to the mean velocity \(U\) and the flow depth \(y\) by the equation \(q = Uy\).
\(\begin{aligned} \frac{d}{d x}\left(\frac{U^{2}}{2 g}\right) &=\frac{d}{d x}\left(\frac{q^{2}}{2 g y^{2}}\right) \\ &=\frac{q^{2}}{2 g} \frac{d}{d x}\left(\frac{1}{y^{2}}\right) \\ &=\frac{q^{2}}{2 g}\left(\frac{-2}{y^{3}}\right) \frac{d y}{d x} \end{aligned}\)
\[=-\frac{q^{2}}{g y^{3}} \frac{d y}{d x} \label{5.27} \]
For later convenience, one more thing needs to be done with this result. Go back to Equation 5.4.9, which gives the relationship between \(q\) and \(y\) that holds when the flow is critical, and write the depth as \(y\) instead of \(d\) (just a matter of notation, as explained above), and substitute that equation into Equation \ref{5.27}. What you get is
\[\frac{d}{d x}\left(\frac{U^{2}}{2 g}\right)=-\frac{y c^{3}}{y^{3}} \frac{d y}{d x} \label{5.28} \]
With regard to the second term on the right in Equation \ref{5.23}, we do not have to do anything further with it, because it just represents the rate of change of flow depth in the downstream direction.
The last term in Equation \ref{5.23} represents the slope of the channel bottom (remember that \(h_{\text{o}}\) was defined as the elevation of the channel bottom), and because in the realm of channel flows the downward slope is arbitrarily defined as positive that last term can just be written \(-S_{\text{o}}\), where \(-S_{\text{o}}\) is the slope of the channel bottom. \(-S_{\text{o}}\) can be written in a form that you will see is useful: think about the hypothetical uniform flow that could pass down the given bottom slope (which, remember, in reality has a nonuniform flow at some different depth passing over it). The depth of this hypothetical uniform flow over any given bottom slope is called the normal depth, \(y_{n}\). Just as with \(S_{e}\), you can express \(-S_{\text{o}}\) in terms of the Chézy equation by using this normal depth \(y_{n}\):
\[S_{\mathrm{o}}=\frac{q^{2}}{C^{2} y_{n}^{3}} \label{5.29} \]
So now, upon substitution of all these reworked forms of the various terms into Equation \ref{5.23}, and then bringing the terms with \(dy/dx\) to the left and the other two to the right, the equation reads as follows:
\[\frac{d y}{d x}\left(1-\frac{y_c^{3}}{y^{3}}\right)=\frac{q^{2}}{C^{2} y_{n}^{3}}-\frac{q^{2}}{C^{2} y^{3}} \label{5.30} \]
Rewrite the second term on the right in the form
\(\frac{q^{2}}{C^{2}\left(\frac{y^{3}}{y_{n}^{3}}\right) y_{n}^{3}}\)
and apply to this term the expression for \(S_{\text{o}}\) given in Equation \ref{5.29} to obtain
\(S_{\text{o}}\left(\frac{y_{n}^{3}}{y^{3}}\right)\)
and substitute that result into Equation \ref{5.30}, replacing the last term back with \(S_{\text{o}}\) also. Finally, solve for \(dy/dx\) to get the grand finale:
\[\frac{d y}{d x}=S_{o} \frac{1-\left(\frac{y_{n}}{y}\right)^{3}}{1-\left(\frac{y_{c}}{y}\right)^{3}} \label{5.31} \]
To get you back on the ground after that tortuous (also torturous?) exercise in manipulation (see Figure \(\PageIndex{1}\) for a summary “road map”), what Equation \ref{5.31} does is give, for a flow that is slowly changing its depth in the downstream direction, the rate of change of depth with downstream distance, as a function of
- The bottom slope \(S_{\text{o}}\)
- The critical depth \(y_{c}\) associated with the given discharge (that is, the flow depth you would see if a flow with that discharge per unit width were in the form of critical flow—which it is not), and
- The normal depth \(y_{n}\) associated with the given discharge (that is, the flow depth you would see if a flow with that bottom slope and that discharge per unit width were uniform—which it is not).
The only thing that stands in the way of perfection is the assumption we made that the friction loss in nonuniform flow at a given depth and discharge is the same as would be seen in the corresponding uniform flow at the same depth and discharge.
People do numerical integrations of Equation \ref{5.31} to get approximate but reasonable water-surface profiles in real gradually varied flows. But what is also commonly done is just to use Equation \ref{5.31} as a qualitative guide to the profile shape to be expected. We will do a little of that here, so that we can finally address the problem of what the water surface looks like as the river runs into the deep reservoir—and that is just one of the many important problems that can be attacked by this approach.
What you need to think about is the sign of \(dy/dx\) on the left side of Equation \ref{5.31}, because if \(dy/dx\) is positive then the flow depth increases downstream, and if \(dy/dx\) is negative then the flow depth decreases downstream— and this is just the information we need in order to keep track of what the water surface does relative to the channel bottom.
The derivative \(dy/dx\) is positive (meaning that the depth increases downstream) if in Equation \ref{5.31} both the numerator and the denominator are positive or if both the numerator and the denominator are negative. Conversely, \(dy/dx\) is negative, and the depth decreases downstream, if the numerator and the denominator have different sign.
Another thing we can do is think about the conditions under which
- \(dy/dx\) becomes zero, meaning that the flow approaches the uniform condition, or
- \(dy/dx\) approaches infinity, meaning that the water surface gets steeper and steeper (obviously, something has to happen before it gets to be vertical!), or
- \(dy/dx\) becomes equal to \(S_{\text{o}}\), meaning that the water surface approaches horizontality.
Suppose that our river flow is subcritical, as is usually the case for large rivers, meaning that the depth is greater than critical and the velocity is less than critical. We can express this by the condition \(y > y_{c}\). So the denominator in the fraction in the right side of Equation \ref{5.31}, which in the following I will call \(F\), is always less than one. With regard to the numerator, you know already that whatever the actual shape of the water-surface profile, the depth must ultimately increase when the reservoir is reached, so \(y > y_{n}\) as well. Also, because we said that the approaching river is subcritical, you know that \(y_{n} > y_{c}\). You can easily convince yourself that these three inequalities guarantee that the fraction \(F\) must be positive and less than one, so \(dy/dx\) is positive and less than \(S_{\text{o}}\), meaning that the depth gradually increases downstream.
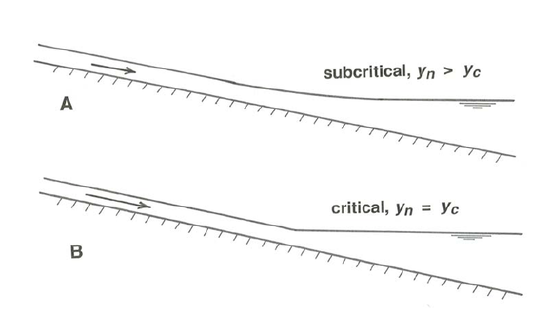
As \(y\) gets larger and larger in the process, both the numerator and the denominator of \(F\) go to one, meaning that \(dy/dx\) goes to \(S_{\text{o}}\), which if you think about it a little bit is the same as saying that the water surface itself becomes horizontal. So our conclusion is that the water-surface profile is as shown in Figure \(\PageIndex{2}\)A: it is asymptotic to the uniform-flow profile upstream, and to the horizontal water surface of the reservoir downstream. This kind of curve is called a backwater curve, for reasons I suppose are obvious.
To carry this analysis just a little further, what is the effect of assuming that the river upstream is flowing at conditions closer to being critical? You can see by inspection of the fraction \(F\) that as \(y_{n} \rightarrow y_{c}\), \(F\) itself stays closer and closer to one for \(y > y_{n}\), meaning that the transition from the almost uniform flow upstream to the horizontal reservoir level downstream is sharper and sharper (that is, it takes place over a shorter and shorter distance), until, for critical flow upstream, the river meets the reservoir at a sharp angle (Figure \(\PageIndex{2}\)B)!
For big rivers flowing well below the critical condition, the backwater effect is felt not just for kilometers but for tens of kilometers upstream, and the superelevation of the actual water surface above the hypothetical point of intersection between the uniform flow and the reservoir level can be many meters. You can imagine the importance of being able to predict the magnitude of this superelevation at all points upstream, when you are worrying about how many homes and farms and businesses you are going to be flooding when you build that dam.
I have just scratched the surface of the business of analyzing backwater effects. There are many qualitatively different kinds of backwater curves, depending upon whether the approaching flow is subcritical, critical, or supercritical, and upon whether
- \(y > y_{n}\) and \(y > y_{c}\),
- \(y\) is between \(y_{n}\) and \(y_{c}\), or
- \(y<y_{n}\) and \(y<y_{c}\).

