5.3: Uniform Flow
- Page ID
- 4178
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Uniform flow serves as a good reference case from which to think about the effect of gravity on the free surface in an open-channel flow. Only if an open- channel flow can somehow be adjusted to be strictly uniform, in the sense that the water surface is planar and the flow depth is the same at all cross sections along the flow (Figure \(\PageIndex{1}\)), can the effect of gravity in shaping the flow be ignored.
Flows in the laboratory can be set up to be very nearly uniform, and outdoors flows like those in long canals are often also close to being uniform. But uniformity is an abstraction: real flows are never perfectly uniform, because, no matter how closely the conditions of flow are adjusted, there are always subtle free-surface effects that extend downstream from the source of the flow and upstream from the sink for the flow, or upstream and downstream from places where the channel geometry changes, like dams or bridge piers.
One kind of problem that is associated with uniform flow is what the channel slope will be if discharge \(Q\), water depth \(d\), and bed sediment size \(D\) are specified or imposed upon the flow. You can investigate this by building an open channel in your back yard, just nailed together out of wood, as if you were going to pan for gold. Try to make the channel several meters long and something like a meter wide, with a planar bottom and planar vertical sidewalls. Immerse the downstream end of the channel in one of those big above-ground swimming pools so many people have in their yards these days. (This is the key to imposing the flow depth on the channel upstream: the higher the water level in the swimming pool relative to the sediment bed in the channel, the deeper the flow in the channel.) Put a submersible pump in the pool to recirculate the water, and the transported sediment as well, to the upstream end of the channel at a given discharge \(Q\). Lay a full bed of sand in the channel, thick enough so that the flow can redistribute it by erosion and deposition if it so desires, without exposing the channel bottom. Mount the upstream end of the channel on a scissors jack or the like, so that you can vary the slope of the channel.
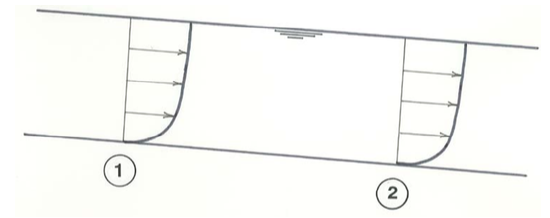
It should seem obvious to you that for a given discharge, and an arbitrary channel-bottom slope you set at the beginning, the flow depth in the channel would vary from upstream to downstream: in general the flow in your channel is nonuniform, before the flow erodes sand from one end of the channel and deposits in at the other end in its desire to establish uniform flow. If that does not seem obvious to you, imagine that for a given discharge you first increased the channel slope; eventually you would have a condition in which the flow was relatively shallow at the upstream end and relatively deep at the downstream end (Figure \(\PageIndex{2}\)A). On the other hand, if you decreased the channel slope to be very gentle, you would eventually have a condition in which the flow was relatively deep at the upstream end and relatively shallow at the downstream end (Figure \(\PageIndex{2}\)B). Somewhere in between those two extreme conditions there would be a slope for which the flow was nearly uniform. The question then is: what governs what the slope is for uniform flow?

The key to the answer lies in flow resistance, which was addressed at length in Chapter 4. But there we analyzed the dynamics of flow resistance after assuming that the flow had already been adjusted for uniformity. Now we are asking how we can predict what the slope will be for uniform flow. This an important engineering problem: if you have to design a drainage culvert or an irrigation channel, you want to make sure that the flow is not grossly non-uniform, or it might end up overflowing its banks either upstream or downstream, and make you vulnerable to lawsuits.
The problem is fairly straightforward. First of all, you have at your disposal the basic resistance equation for open-channel flow (Equation 4.2.1, repeated here):
\[\tau_{0}=\gamma d \sin \alpha \label{5.1} \]
You also have an empirical equation for bed shear stress \(\tau_{\text{o}}\) in terms of a resistance coefficient, which could be the friction factor \(f\) or the Chézy coefficient \(C\) (Equation 4.6.1, repeated here in slightly rearranged form):
\[\tau_{0}=\frac{f}{8} \rho U^{2} \label{5.2} \]
You also know the mean velocity \(U\), because you have chosen \(Q\) yourself and you already know \(d\), so by the relation \(Q = Ud b\) (where \(b\) is the known width of the channel) you can solve for \(U\). Compute the mean-flow Reynolds number \(\text{Re}\), go to a diagram like that in Figure 4.7.7 (that diagram was found for flow in a circular pipe, but it is known to give fairly good results for open-channel flow, provided that you use the hydraulic radius both for the channel flow and for the pipe flow) to find \(f\) and thus, by Equation \ref{5.2}, \(\tau_{\text{o}}\). Then, knowing \(\tau_{\text{o}}\), you can use Equation \ref{5.1} to find the slope angle \(\alpha\). You could adjust the channel slope by use of your scissors jack—and you would have to do that if the channel bottom is rigid rather than mantled with loose sediment—but with the full bed of sediment, the flow eventually adjusts the slope to the condition of uniform flow by eroding sediment and one end and depositing sediment at the other end.
Now for a further aspect of uniform flow, one that is more relevant to natural open-channel flows on the Earth’s surface. Excavate a very long, straight channel, ending at the brink of a large, deep, open pit into which the flow will fall freely, on a gently and uniformly sloping area of the land surface. A length of many kilometers would be good. Arrange to pass a discharge \(Q\) of your choosing down the channel. You can readily appreciate that if the channel is sufficiently long the flow in the channel will be close to being uniform, although you can assist the approach to uniformity by fiddling a bit with the flow at the downstream end, by installing a sluice gate or a porous weir to prevent the decrease in upstream depth as the flow falls out of the channel. You will also have to be prepared to feed in some bed sediment at the upstream end, to replenish what is transported down the channel and out the end, if the flow turns out to be strong enough to move some of the sediment. Otherwise, you would be modeling the long-term behavior of a real river, whereby the river gradually wears down the land area on which it flows, thus decreasing the slope of the land over the long term.
The big question now is: what will the uniform flow depth be, given the imposed slope and discharge? Is the flow fast and shallow, or is it slow and deep? You have the same hydraulic relationships available as in the previous situation, but now their application is not as straightforward. Think about what you know and what you do not know. What is given is the slope angle \(\alpha\), the discharge \(Q\), the bed sediment size \(D\), and the channel width \(b\) The unknowns are the mean flow velocity \(U\), the flow depth \(d\), the resistance coefficient or friction factor \(f\), and the boundary shear stress \(\tau_{\text{o}}\). You have four relationships available that involve these knowns and unknowns:
- \(\tau_{text{o}}=\gamma d \sin \alpha\) (the basic resistance equation for uniform channel flow)
- \(Q = Ud b\) (conservation of flow volume)
- \(\tau_{0}=(f / 8) \rho U^{2}\) (the relationship between flow velocity and boundary shear stress)
- \(f = f(\text{Re}, D/d)\) (the dependence of the friction coefficient on flow velocity, flow depth, and bed roughness)
These are the same equations used in the earlier situation. The difference is that you cannot proceed step by step to find the answer: you need to deal with them all at once. The problem is well posed (four unknowns, four equations), but you cannot obtain the solution analytically, in closed form; you need to find the solution by some iterative numerical technique. The important point here, though, is that there is a unique solution: for any given combination of channel slope, bed sediment, and water discharge, there is a certain flow depth, mean flow velocity, and boundary shear stress. And your intuition tells you, correctly in this case, that the uniform flow depth increases with water discharge and also with bed roughness: the greater the discharge, and the rougher the bed (meaning more resistance to flow), the greater the flow depth for uniform flow. It is clear also that the flow depth depends on the slope: the greater the slope, the smaller the flow depth.

