14.2: D.2- Initiation of transport and damage

In Sect. 6.3 the ‘initiation of transport’ concept of Shields (1936) was introduced for sediment particles under the impact of uniform flow. The parameter (\(\theta\)) that he introduced is the ratio of the drag force due to the flow over the resisting force due to the underwater weight of the sediment. Initiation of motion occurs for a value of this parameter (\(\theta_{cr}\), Eq. 6.3.1.3) between 0.03 and 0.05 in practice. When, at a later stage, sediment transport formulas for uniform flow started to be developed, it turned out that Shields’ parameter was not only a good parameter to describe threshold of motion but also a fundamental parameter in empirical transport formulas that nearly all can be expressed as a power function of \(\theta\) or \((\theta - \theta_{cr})\), with the power ranging from 1.5 to 3 (see Sect. 6.5). That is why \(\theta\) or \((\theta - \theta_{cr})\), is often referred to as the mobility number.

Sleath (1978) evaluated initiation of sediment motion under oscillatory flow from literature and his own experiments, and could show that by using the velocity amplitude (say the orbital velocity amplitude) a ‘Shields’ parameter for waves could be derived where the empirical values for the initiation of motion only differ marginally from \(\theta_{cr}\), viz. in the range 0.02 to 0.05.

Interestingly, Iribarren (1938), two years after Shields’ publication and most likely independent from him, proposed a stability criterion for a sloping rubble mound breakwater. The breakwater is stable if:

\[\underbrace{rho_s g D^3}_{\text{stone weight}} \ge \dfrac{N \rho_s g H^3}{\Delta^3 (\mu \cos \alpha \pm \sin \alpha)^3}\]

in which the friction coefficient \(\mu = \tan \varphi_r\) with \(\varphi_r\) is the natural angle of repose, \(\Delta = (\rho_s - \rho)/\rho\), \(\alpha\) is the angle of the bed slope, \(H\) is the wave height and \(N\) is a coefficient. The density \(\rho_s\) should now be interpreted as the density of the blocks (rock) and \(D\) as a characteristic stone size.

We can rewrite this equation as:

\[\dfrac{H}{\Delta D(\mu \cos \alpha \pm \sin \alpha)} = \dfrac{\rho g D^2 H}{(\rho_s - \rho) g D^3 (\tan \varphi_r \cos \alpha \pm \sin \alpha)} \le \dfrac{1}{\sqrt[3]{N}}\label{eq14.2.2}\]

In the second term of this equation we can now recognize the ratio of drag force over the resisting force, similarly as Shields used (see Sect. 6.3.1). The numerator represents the drag force \(\rho u^2 D^2\) taking as a characteristic value for \(u = \sqrt{gH}\) (wave height order of magnitude of the water depth). The denominator reflects the resisting force proportional to \((\rho_s - \rho) g D^3\). We further find in the denominator the effect of the bed slope, where the plus sign is for up-rush and the minus sign for down-rush. Once \(\alpha\) approaches the natural angle of repose \(\varphi_r\), the resisting force approaches zero for downrush. Further note the correspondence between the slope correction \(\tan \varphi_r \cos \alpha \pm \sin \alpha\) and the denominator of Eq. 6.7.2.4.

We can write Eq. \(\ref{eq14.2.2}\) as a slope-dependent criterion for initiation of movement of a block of a certain size:

\[\dfrac{H_{cr}}{\Delta D} = \dfrac{\mu \cos \alpha \pm \sin \alpha}{\sqrt[3]{N}}\label{eq14.2.3}\]

Later, many experiments were performed, mostly by Hudson (1952), to find the constants of proportionality in Eq. \(\ref{eq14.2.3}\). For practical reasons, Hudson finally proposed a criterion in which he indicated the proportionality constant as \(K_D\) and in which he changed the slope correction term to \(cot \alpha\).

\[\dfrac{H_{cr}}{\Delta D} = (K_D \cot \alpha )^{1/3}\]

Note that what \(\theta_{cr}\) is for initiation of motion of sediment, \((K_D \cot \alpha)^{1/3}\) is for initiation of damage on a rocky slope. Both parameters are based on the same stability principle. Hudson’s not physically based slope correction term limits the validity of this world-wide applied formula to the range of \(1.5 < \cot \alpha < 4\).

Just like the values of the Shields parameter, the values of \(K_D\) are based on experiments. Because structures represent a physically much more complex system than a flat sandy bed, the range of \(K_D\) values is larger. For instance, for natural rock \(K_D\) is 3-4 and for artificial elements like Tetrapods or Xblocs®it is 8-10. The latter higher values are due to the interlocking effect.

This would lead to values for \((K_D \cot \alpha)^{1/3}\) within the range of 1.5 to 3.5 and thus two orders of magnitude larger than the critical Shields parameter. What is the reason of this difference? To answer that, we rewrite the Shields parameter using \(u = \sqrt{gH}\) as follows:

\[\theta = \dfrac{\tau_b}{(\rho_s - \rho) gD} = \dfrac{\rho c_f u^2}{(\rho_s - \rho) gD} = c_f \dfrac{H}{\Delta D}\]

Hence, the Shields parameter is related to \(H/\Delta D\) through a friction factor \(c_f\) (order of magnitude \(10^{-2}\)). This would lead to values for the critical Shields parameter that are two order of magnitude smaller than critical values of \((K_D \cot \alpha)^{1/3}\), which agrees with the above mentioned typical ranges.

The simplicity of Hudson is very attractive, but the complex physics of rubble mound structures makes that these physics can only be included empirically in the \(K_D\) coefficient. These physics are in the loading, the structure’s geometry and its permeability. Van der Meer (1988) conducted a lot of empirical research varying these physical conditions and arrived at expressions for \((K_D \cot \alpha)^{1/3}\) where this parameter is a function of the structure’s slope, the type of wave breaking (Iribarren number), the number of waves, the permeability and the progressive damage.

As an example we present the equation of Van der Meer (1988) for plunging breakers on a loose rock slope in which the right hand term is a fit to \((K_D \cot \alpha)^{1/3}\) that includes the permeability (\(P\)), the damage (\(S\)), the number waves (\(N\)) and the type of wave breaking (\(\xi\), the Iribarren parameter Eq. 5.2.5.5, which includes the slope, a property of the structure’s geometry):

\[H_{s, cr}/(\Delta D) = 6.2 P^{0.18} (S/\sqrt{N})^{0.2} \xi^{-0.5}\label{eq14.2.6}\]

Figure D.1: Damage curve according to Eq. \(\ref{eq14.2.6}\) with \(P = 0.5\) for a permeable core, \(N = 3000\) (which for an average period of 6 s represents a storm of 5 hours duration) and \(\xi = 2\).

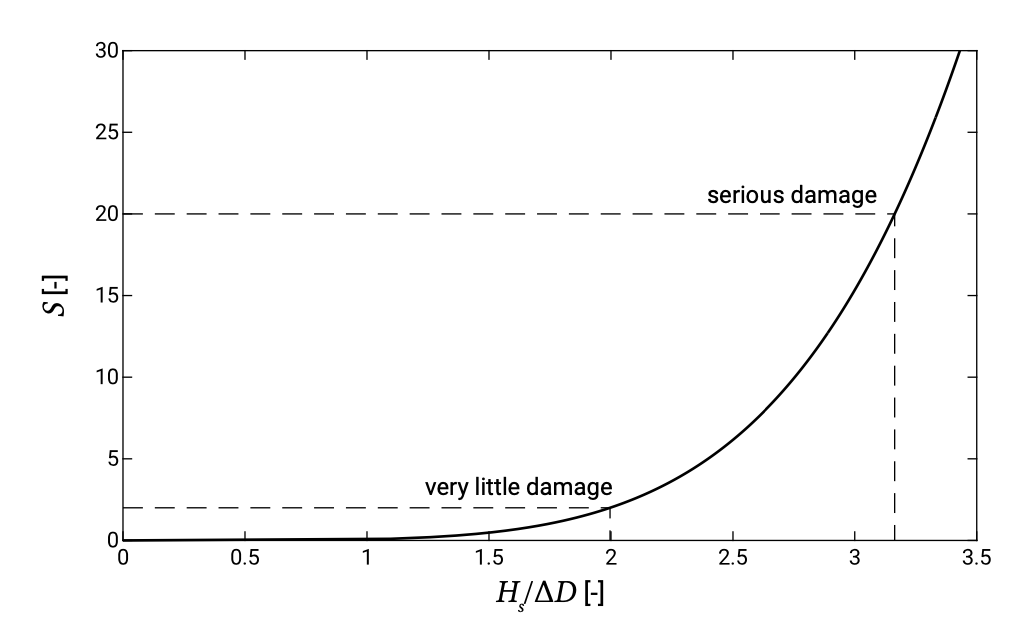
Typically this leads to the progressive damage curve as shown in Fig. D.1. Note \(S = 2\) means very little damage and \(S = 20\) means serious damage.

In sediment transport terms, i.e. we solve for the damage that may be interpreted as transport, we may rewrite Eq. \(\ref{eq14.2.6}\) to:

\[S = (6.2 P^{0.18})^{-5} \sqrt{N} \xi^{2.5} (H_s /\Delta D)^5\]

Note that damage is now included in a wider meaning, namely the damage can now vary from initiation of motion to larger amounts of motion or ‘transport’. It appears that the damage is proportional to the power 5 of the Hudson parameter. Again we see a similarity with sediment in that \(H_s/\Delta D\) is used as a mobility number, so that we are talking about transport.