6.3.1: Forces on a single grain

Sediment can only be transported if the water movement exerts a large enough shear stress \(\tau_b\) on the grains. The so-called critical shear stress \(\tau_{b, cr}\) describes the point of initiation of motion. If this condition is exceeded, grains move, roll or are brought into suspension. Note that instead of the term bed shear stress one may find the term shear velocity (\(u_*\)), which is related to the bed shear stress through \(\tau_b = \rho u_* |u_*|\).

Figure 6.4: Forces on an individual grain in a stationary situation.

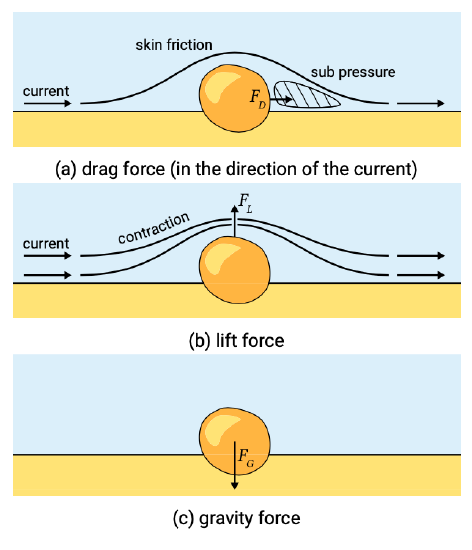
In order to assess the critical condition of initiation of motion, the various forces acting on an individual grain have to be taken into account (see Fig. 6.4). These forces can be divided into forces which tend to move the grain – the drag force \(F_D\) (Fig. 6.4a) and the lift force \(F_L\) (Fig. 6.4b) – and a force which tries to keep the grain in its place; the gravity force \(F_G\) (Fig. 6.4c).

The drag force is a combination of skin friction acting on the surface of the grain and a pressure difference on the up and downstream sides of the grain because of flow separation at the downstream end of the particle. Analogous to Eq. 6.2.3.2, the drag force is proportional to:

• the square \(u^2\) of a characteristic upstream horizontal flow velocity;
• the particle’s surface area and hence for spheres to \(D^2\)
• the water density \(\rho\)

The lift force results from the flow separation as well as from the flow contraction above the grain. A higher local flow velocity results in a lower local pressure (Bernoulli law). The difference in vertical pressure causes an upward directed lift force. Similarly to the drag force, the lift force is proportional to the particle's surface area (and thus to \(D^2\) in the case of a sphere) and to \(u^2\).

The total driving force (drag and lift combined) is therefore proportional to \(\rho u^2 D^2\). The resisting gravity force is proportional to \((\rho_s - \rho)g D^3\) (see Eq. 6.2.3.1). Equilibrium of forces, whether horizontal, vertical or rotational, therefore gives an expression of the form:

\[(\rho_s - \rho) g D^3 \propto \rho u_{cr}^2 D^2\]

in which \(u_{cr}\) is the critical velocity of the water at which grains start moving. Since the bed shear stress is proportional to the velocity squared times the water density, we could also write:

\[(\rho_s - \rho) g D^3 \propto \rho \tau_{b, cr} D^2\label{eq6.3.1.2}\]

Here, \(\tau_{b, cr} = \rho u_{*, cr}^2\) is the critical bottom shear stress (critical in the sense that higher bottom shear stresses lead to the initiation of motion).

From the proportionality Eq. \(\ref{eq6.3.1.2}\), the so-called critical Shields parameter \(\theta_{cr}\) can be deduced:

\[\theta_{cr} = \dfrac{\tau_{b, cr}}{(\rho_s - \rho) g D} = C\label{eq6.3.1.3}\]

The constant \(C\) has to be determined experimentally. The experiments of Shields, performed on a flat bed, are the most widely used. He defined the critical bed shear stress as the bed shear stress at which the (extrapolated) measured transport rates were just zero. For sand placed smoothly on this flat bed, \(C\) was found to be around 0.05. Appendix D points out the similarities between Eq. \(\ref{eq6.3.1.3}\) and stone stability and structural damage approaches for slopes of loose rock and of breakwater elements.