6.5.2: Including waves
- Page ID
- 16352
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For nearshore applications the influence of waves needs to be included into the Shields parameter. This can be done in two ways, either by using the time-averaged (wave-averaged) bed shear stress for the combined wave-current motion or by using the instantaneous bed shear stress (varying during the wave motion). Both approaches will be explained below.
The instantaneous bed load transport vector \(S_b\) for waves and currents combined can be written in a dimensionless form as:
\[\Phi_b (t) = \sqrt{\dfrac{S_b (t)}{(s - 1) g D_{50}^3}}\label{eq6.5.2.1}\]
This dimensionless formulation has been proposed by Einstein (1942, 1950) based on theoretical considerations. The denominator is the square-root of a parameter representing the specific underwater weight of sand grains. Further, \(S_b\) is the bed-load transport rate in volume per unit time and width. In applying a certain formulation one should check whether \(S_b\) is defined including pores or excluding pores.
Based on the above we can expect that the instantaneous dimensionless bed load transport \(\Phi_b (t)\) responds quasi-steadily to the instantaneous bed shear stress (above the threshold or the critical bed shear stress). Hence,
\[\Phi_b (t) = f(\theta' (t), \theta_{cr})\label{eq6.5.2.2}\]
in which \(f\) is an algebraic operator and \(\theta_{cr}\) is defined by Eq. 6.3.1.3. The instantaneous dimensionless effective shear stress \(\theta' (t)\) due to currents and waves is given by:
\[\theta' (t) = \dfrac{\tau_b'}{(\rho_s - \rho) g D_{50}}\label{eq6.5.2.3}\]
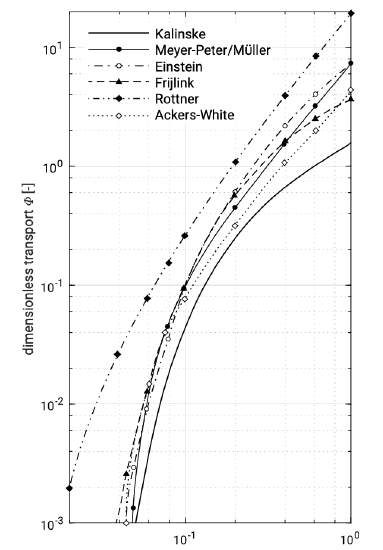
skin friction \(\theta'\) (see Eq. \(\ref{eq6.5.2.3}\))
Figure 6.11: Comparison of various bed-load transport formulas developed for rivers. On the \(y\)-axis is the dimensionless transport Φ in the case of steady flow (cf. Eq. \(\ref{eq6.5.2.1}\)), on the \(x\)-axis a Shields parameter based on skin friction (cf. Eq. \(\ref{eq6.5.2.3}\)). Note that \(\Delta = (\rho_s - \rho)/\rho\) and the subscript 0 to the shear stress refers to the bed shear stress. Adapted from Breusers (1983).
The Shields parameter \(\theta'\) is a measure of the forcing on the sediment grains (drag and lift) relative to the resisting force (see Sect. 6.3.1). The effective bed-shear stress \(\tau_b'\) is that part of the total bed shear stress which is transferred directly to the grains in the bed as skin friction. The form drag induced by bed forms is not effective in relation to bed load transportation. One way to compute the skin friction is to use a roughness height related to the grain size and not to the bed form size. Also, so-called efficiency or ripple factors \(\mu\) can be used that represent the fraction of the total bed-shear stress that can be attributed to skin friction. The latter approach was followed in Fig. 6.11.
The non-dimensional critical shear stress parameter \(\theta_{cr}\) represents the threshold of motion of sand grains. It can be computed using the classical Shields curve (Fig. 6.5) or an explicit approximation of the form Eq. 6.3.2.3.
Time-averaging Eq. \(\ref{eq6.5.2.2}\) gives a time-averaged bed load sediment transport:
\[\langle \Phi_b (t) \rangle = \langle f (\theta' (t), \theta_{cr}) \rangle\label{eq6.5.2.4}\]
The brackets \(\langle \ \rangle\) denote time-averaging.
Some time-averaged formulations for bed load transport relate the time-averaged bed load transport directly to a time-averaged bed shear stress magnitude (averaged over the wave motion) instead of to an instantaneous bed shear stress:
\[\langle \Phi_b (t) \rangle = f (\langle | \theta' (t)|\rangle, \theta_{cr})\label{eq6.5.2.5}\]
Note the differences between Eqs. \(\ref{eq6.5.2.4}\) and \(\ref{eq6.5.2.5}\).
By correlation of the non-dimensional parameters in Eqs. \(\ref{eq6.5.2.4}\) and \(\ref{eq6.5.2.5}\), using a range of datasets of sediment transport, a general bed-load transport formula can be obtained. Many of those exist, based on different data sets and correlating different parameters.


