6.3.2: Shields curve
- Page ID
- 16348
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Shields found that the ‘constant’ was a weak function of the grain Reynolds number defined as:
\[\text{R e}_* = \dfrac{u_* D}{v}\]
where:
| \(u_*\) | shear stress velocity | \(m/s\) |
| \(D\) | diameter of grains | \(m\) |
| \(v\) | kinematic viscosity coefficient | \(m^2/s\) |
The subscript * is used to indicate that the Reynolds number is based on \(u_*\).
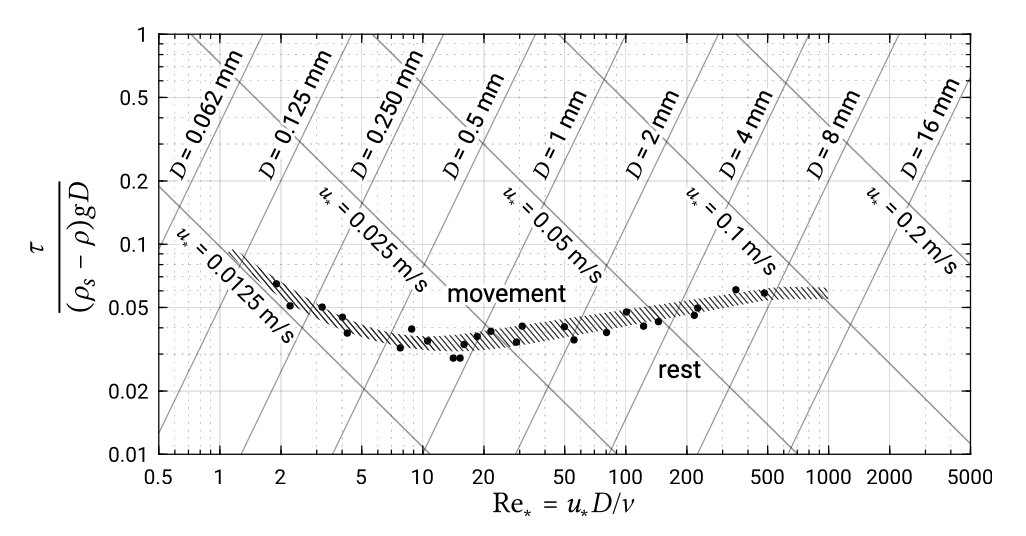
Figure 6.5: Shields curve (Shields, 1936). Note that the axes are drawn on a log-log scale. The lines of constant \(D\) and \(u_*\) do not originate from Shields and hold for constant density \(\rho_s = 2650\ kg/m^3\) and kinematic viscosity \(v = 1.25 \times 10^{-6}\ m^2/s\) at a water temperature of 12 °C.
Figure 6.5 shows measured values of 𝐶 as a function of \(\text{R e}_*\). The shaded band separates two zones: movement of sediment particles was observed in the experiments in the zone above this shaded band, whereas no movement was observed in the zone underneath the shaded band. The shaded band therefore indicates initiation of motion. Sometimes, the shaded band is represented by a single line, which is then referred to as the Shields curve. The average value can be seen to be approximately 0.05.
Unfortunately, reality is more complex. Amongst others:
-
The Shields curve is valid for uniform flow on a flat bed. The effect of bed ripples and the effect of the combination of unidirectional and oscillatory flow on initiation of motion are largely unknown;
-
Gradation of the bed material may play a role, especially for poorly sorted sediment (\(D_{90}/D_{10} > 3\)). In these cases, the smaller particles will be hidden in the voids between the larger particles, while the larger particles are more exposed. After exposed smaller particles are washed out, a top layer of coarser particles (with higher critical flow velocities) remains and prevents the movement of the underlying smaller particles. This is called bed armouring;
-
For a sloping bed in the flow direction, it can be argued that the critical flow velocity will be somewhat smaller for downward sloping beds and somewhat higher for upward sloping beds;
-
Cohesive forces between the grains – due to the presence of cohesive sediment in the bed – may drastically increase the resistance against erosion (see also Sect. 6.8). Biological activity and consolidation may be important in this respect as well.
Notwithstanding these complications, many practical sediment transport formulations use the critical Shields parameter \(\theta_{cr}\) (Eq. 6.3.1.3) and the Shields curve to define initiation of motion. Amongst others Van Rijn (1984a) has represented the Shields curve as a function of a non-dimensional grain size \(D_*\):
\[D_* = D_{\text{so}} \left (\dfrac{g(s - 1)}{v^2} \right )^{1/3}\]
The Shields curve can be represented in terms of \(D_*\) since every grain diameter has a corresponding \(u_{*, cr}\) as can be seen in Fig. 6.5. With \(\theta_{cr} = f (D_*)\), no iteration is necessary to obtain the critical shear stress, as would be the case when applying the Shields curve. In addition, the threshold parameter can be corrected to account for the effect of the bed slope \(\tan \alpha\) on the threshold of motion. This formulation results in an increase of the critical shear stress for upslope movement and a decrease of the critical shear stress for downslope movement. We then have a formulation of the form:
\[\theta_{cr} = f (D_*, \tan \alpha)\]


