3.7.2: Gravitational pull
- Page ID
- 16300
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)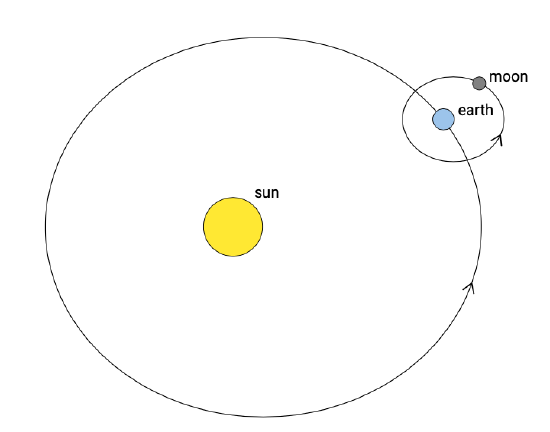
The tide-generating forces find their origin in the gravitational pull of the moon and the sun on the water in the oceans. The sun and the earth revolve around a common centre of gravity. They attract each other by a force that is proportional to the masses and inversely proportional to the square of their distance. Similarly, the moon and the earth revolve around their common centre of gravity. Revolving about a common centre of mass implies that the attraction forces act as centripetal forces, so that the earth is constantly being accelerated towards the moon and the sun, as in free fall, the direction of the free fall being everywhere parallel to the line connecting the gravitational centres. The difference in mass between the sun and the moon causes the gravitation centre of the earth-sun system to be located inside the sun, and the centre of the earth-moon system within the earth. In a simplification, we can therefore say that the earth circles around the sun and that the moon circles around the earth (see Fig. 3.16).
At the same time the earth rotates around its own axis in the same direction as the earth orbits the sun and the moon orbits the earth. The periods of these motions are explained in Intermezzo 3.3.
| mass of the sun | \(1.99 \times 10^{30}\ kg\) |
| mass of the earth | \(5.98 \times 10^{24}\ kg\) |
| mass of the moon | \(7.35 \times 10^{22}\ kg\) |
| distance between (centres of) the sun and the earth | \(1.50 \times 10^{8}\ km\) |
| distance between (centres of) the earth and the moon | \(3.84 \times 10^5 \ km\) |
| radius of the earth | \(6.37 \times 10^3 \ km\) |
The gravitational pull of the sun on 1 kg of mass of the earth using the average distance between the sun and the earth of \(d_s = 1.5 \times 10^{11}\ m\) is:
\[a_s = G\dfrac{M_s}{d_s^2} = 6.0 \times 10^{-4} g \label{eq3.7.2.1}\]
where \(G = 6.6 \times 10^{-11}\ Nm^2/kg\) is the universal gravitational constant and \(g = 9.81\ N/kg\) (or equivalently \(m/s^2\)) is the gravitational pull of the earth itself at the surface of the earth. Similarly, the gravitational pull of the moon on 1 kg of mass of the earth at an average distance of \(d_m = 3.84 \times 10^8\ m\) is:
\[a_m = G \dfrac{M_m}{d_m^2} = 3.4 \times 10^{-6} g \label{eq3.7.2.2}\]
Note that Eqs. \(\ref{eq3.7.2.1}\) and \(\ref{eq3.7.2.2}\) represent the gravitational acceleration (force per unit mass) for the centre of the earth. As such, they represent the attraction of the earth as a whole towards the sun and the moon (considering the mass of the earth concentrated at the earth’s centre of mass).
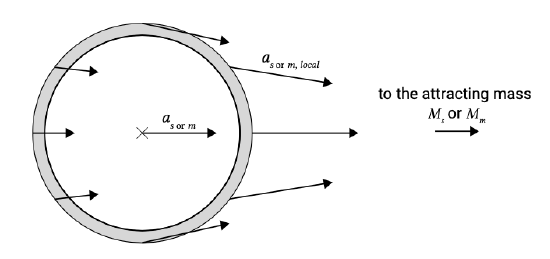
For different locations at the earth’s surface the magnitude and direction of the gravitational acceleration slightly differ from each other and from the acceleration of the earth’s centre due to varying distances and angles to the centre of the attracting mass (see Fig. 3.17).
Summarizing, the gravitational attraction provides the centripetal acceleration that maintains the motion of the earth around the centre of gravity of the earth-sun (earth-moon) system. For every point on earth, this centripetal acceleration of the earth in free fall towards the sun (moon) is directed parallel to the line connecting the centres of the earth and the sun (moon). Its magnitude is determined by the gravitational acceleration \(a_s (a_m)\) of the sun (moon) on the earth’s centre as given by Eq. \(\ref{eq3.7.2.1}\) (Eq. \(\ref{eq3.7.2.2}\)). But nowhere at the surface of the earth is the gravitational acceleration exactly equal in magnitude and direction to the centripetal acceleration.


