3.7.3: Differential pull or the tide-generating force

Equations 3.7.2.1 and 3.7.2.2 show that the sun’s gravitational pull is two orders of magnitude larger than the moon’s gravitational pull. This we could have expected since the earth orbits the sun and not the moon. Nevertheless, the sun contributes only to about 30% of the tidal amplitudes in the oceans and the moon is responsible for the remaining 70%. The reason is that it is not the gravitational pull per se that is responsible for the tide-generating forces.

In the above we have seen that the gravitational attraction provides the centripetal acceleration that maintains the motion of the earth around the centre of gravity of the earth-sun (earth-moon) system. With the gravitational attraction for the earth as a whole (Eqs. 3.7.2.1 and 3.7.2.2) accounted for⁴, the tide is generated by a much subtler effect, i.e. the difference between the gravitational pull on ocean water masses that are located at different distances from the sun and the moon.

Consider 1 kg of mass on the near side of the earth which therefore is the earth’s radius \(R = 6.37 \times 10^6\) m closer to the sun than the centre of the earth is. The gravitational pull of the sun on 1 kg of mass on the near side of the earth is \(\Delta a_s\) greater than \(a_s\), i.e.:

\[\begin{array} {c} {\Delta a_s = a_{s, near\ side} -a_s = G \dfrac{M_s}{(d_s - R)^2} - G \dfrac{M_s}{d_s^2} \approx} \\ {2G \dfrac{M_s R}{d_s^3} = a_s \dfrac{2R}{d_s} = 0.515 \times 10^{-7} g} \end{array}\]

This is known as differential pull. Note that \(a_s\) is to first order inversely proportional to the cube of the distance. Similarly for the moon:

\[\Delta a_m \approx 2G \dfrac{M_m R}{d_m^3} = a_m \dfrac{2R}{d_m} = 1.13 \times 10^{-7} g\]

Figure 3.18: The direction and relative magnitudes of the differential gravitational pull at different locations on the earth’s surface. At each location, it is given by the vector subtraction of \(a_{s \ or \ m, local}\) and the part \(a_{s \ or \ m}\) that provides the centripetal acceleration. The depicted tidal bulges result from the tangential components of the differential pull (see Fig. 3.19).

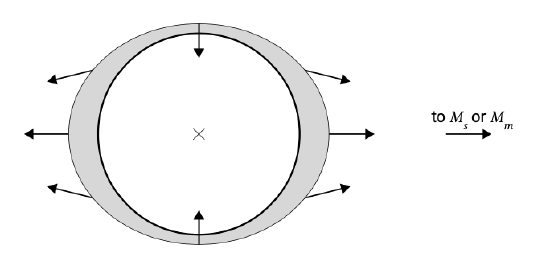
The point furthest from the sun (moon) is in turn smaller than \(a_s (a_m)\) by the same amount \(\Delta a_s (\Delta a_m)\) which can be shown by a similar calculation. Carrying out the calculation for all places on the earth leads to a differential pull on the earth as indicated schematically in Fig. 3.18 (compare with Fig. 3.17).

The differential pull is responsible for the tidal generation and is therefore also referred to as tidal force. Since \(\Delta a\) is proportional to \(M/d^3\) the solar differential pull \(\Delta a_s\) is only 0.46 times the lunar differential pull \(\Delta a_m\). The moon is responsible for 69% of the tidal mechanism as \(\Delta a_m /(\Delta a_m + \Delta a_s)\) = 69%.

Figure 3.19: The horizontal component of the tidal force on the earth when the tide-generating body (the earth or the moon) is above the equator at \(z\).

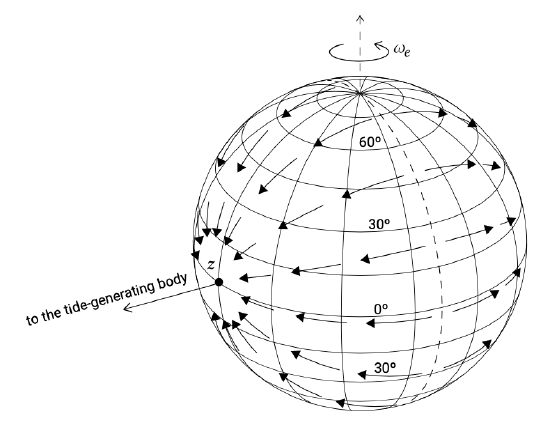
The differential pull as sketched in Fig. 3.18 has components normal and parallel to the earth’s surface. The normal components are many orders of magnitude smaller than the earth’s own gravitational attraction. For example for the point closest to the sun the differential acceleration is normal to the earth surface and with a magnitude of \(0.515 \times 10^{-7} g\) it is negligible compared to \(g\). The tangential or ‘horizontal’ components are of the same order of magnitude as the normal components, but since they are perpendicular to the earth’s gravity field they cannot be neglected. The tangential forces are demonstrated in Fig. 3.19.

The effect of the tangential forces is to shift water to the side of the earth facing the sun (moon) and to the opposite side in tidal bulges (see Fig. 3.18). The piling up of water due to the tangential forces is balanced by pressure gradients in the opposite direction due to the sloping water surface. If the earth were completely covered by water, its equilibrium configuration would be an ellipsoid (rugby ball or egg).

The rapid diurnal rotation of the earth around its own axis makes the earth rotate underneath the tidal bulges, thus producing a semi-diurnal tide with two high and two low waters passing the same point on the earth every day. The period of the solar tide is exactly 12 h (our day is measured in terms of the sun, Intermezzo 3.3). The period of the lunar tide is governed by the period between the moon phases or the lunar day. The period of the semi-diurnal lunar tide is thus equal to half a lunar day = 12 hours and 25 minutes.

Intermezzo 3.3: Movements of the earth, earth-moon and earth-sun system

The earth circles the sun in 365.25 days. The earth rotates around its own axis in 23 hours and 56 minutes (sidereal day, relative to the stars) in the same direction in which the moon is revolving around the earth and the earth around the sun. While the earth completes one daily rotation, the earth also revolves with respect to the sun. As a result it is only after 24 hours or one (solar) day that the earth returns in the same position with respect to the sun as seen by an observer on the earth. A lunar day lasts even longer, viz. 24 hours and 50 minutes. This occurs because the moon progresses in its orbit around the earth during earth’s daily rotation. The extra 50 minutes are required for the earth to ‘catch up’ with the moon, as will be explained below.

The period of the moon’s revolution around the earth is 27.3 days (sidereal month). The moon takes 29.5 days to return to the same position relative to the sun as seen by an observer on the earth. Such a lunar month is the time between successive recurrences of the same phase; e.g., between full moon and full moon. During the 27.3 days of the sidereal month, the earth has moved along in its orbit around the sun and now the moon must ‘catch up’ to this new position. It takes 2.2 days to do so.

Figure 3.20: A lunar day (the time between successive transits of the moon for an observer on the earth) is 24 hours and 50 minutes.

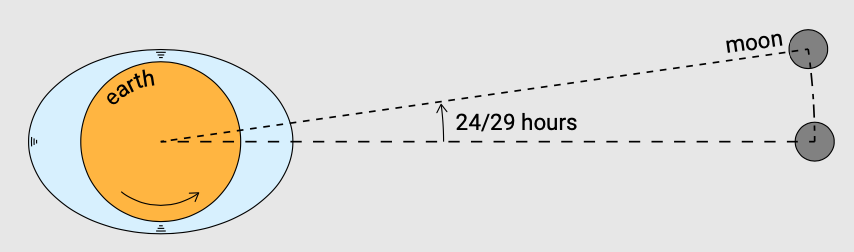
Further, while the moon progresses in its orbit around the earth, the earth rotates around its own axis. The earth must rotate a bit more than a full rotation before any given location ‘catches up’ with the lunar bulge. During one rotation of the earth around its axis, the moon has covered 1/29.5th of its total orbit around the earth (with respect to the sun). Therefore, a lunar day is equal to \((1 + 1/29.5) \times 24\) h = 24 h 50 min. Figure 3.20 shows the required additional rotation of the earth to catch up with the moon.

---

4. Alternative but equivalent explanations (see your DUT lecture notes of CTB2410 and CIE5317) take the moving earth as a reference frame and introduce ‘fictitious’ centrifugal forces (see also Intermezzo 3.1). Due to the revolution of the earth around the centre of gravity of the earth-sun (earth-moon) system, there is an outward directed centrifugal force that is the same at every point on the earth and directed parallel to the line of centres. The centrifugal acceleration (force per unit mass) balances the gravitational acceleration of the earth’s centre towards the sun (moon).