3.4.4: Short-term wave height distribution
- Page ID
- 16292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the previous section we have seen that in deep water and as long as the waves are not too steep, the surface elevation can be considered as the sum of a large number of components with random phases. In that case observations and theoretical considerations have shown that the wave heights can be described by a Rayleigh distribution. We will see below that by using the Rayleigh distribution the parameters as determined by the wave-by-wave analysis and by the spectral analysis can be related to each other.
The short-term distribution of wave heights known as the Rayleigh distribution is:
\[p(H) = \dfrac{H}{4\sigma^2} e^{-\tfrac{H^2}{8\sigma^2}}\label{eq3.4.4.1}\]
Although theoretically only valid for a narrow spectrum, observations have shown that also for broader spectra the wave heights more or less obey a Rayleigh distribution. In practice wave period variability is often ignored.
From the probability density function (Eq. \(\ref{eq3.4.4.1}\)) the probability can be derived that an individual wave height \(H'\) exceeds a specified wave height \(H\):
\[P(H' > H) = 1 - P(H' < H) = 1 - \int_{0}^{H} p(H) dH = e^{-\tfrac{H^2}{8\sigma^2}}\label{eq3.4.4.2}\]
where the only parameter \(\sigma\) is the standard deviation and thus a wave height measure. As we have seen it can be estimated from either the time-series or, since \(\sigma = \sqrt{m_0}\), from the spectrum.
The wave height with a probability of exceedance \(P\) follows from Eq. \(\ref{eq3.4.4.2}\):
\[H_P = 2 \sigma \sqrt{2\ln (1/P)} \label{eq3.4.4.3}\]
For instance, the height \(H_{2\%}\) that is exceeded by 2% of the waves is equal to \(2\sigma \sqrt{2\ln (1/P)}\) and \(H_{1\%} = 6.07 \sigma\).
In Sect. 3.4.3 \(H_{1/3}\) was calculated from the time-series. We can also use the Rayleigh distribution to calculate \(H_{1/3}\). This can be shown to yield:
\[H_{1/3} = 4\sigma \label{eq3.4.4.4}\]
The probability of exceedance of wave heights according to the Rayleigh distribution can now be expressed in terms of significant wave height also:
\[P(H' > H) = e^{-2(\tfrac{H}{H_s})^2}\]
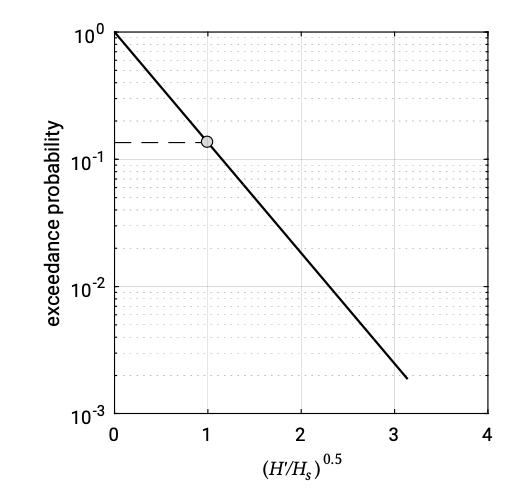
Figure 3.8: On Rayleigh paper (with a log-scale vertical axis) the Rayleigh distribution is represented by a straight line through the origin.
which is often graphically represented as in Fig. 3.8.
The value of \(H_s\) can be read from the graph at the 13.5% exceedance value (\(e^{-2}\)). It also follows that 1 out of 100 waves will be higher than about 1.5 times \(H_s\). The strength of the storm considered is apparently determined by just one value: \(H_s\). A stronger storm would lead to a steeper distribution curve, which is again defined by a specific value of the significant wave height.
When irregular waves enter shallow water, the highest waves will start breaking due to the limited depth. This means that the Rayleigh distribution is no longer applicable for \(H_s > 0.3h\) or so. Then for the tail of the distribution a Weibull distribution agrees better.
Based on Eq. \(\ref{eq3.4.4.4}\) we define \(H_{m_0} = 4\sqrt{m_0}\) as an alternative expression to calculate the significant wave height and use the subscript \(m_0\) to indicate that the wave height is computed from the zero-moment of the wave spectrum. By the way, from observations at sea it appears that a correction to this theoretical value gives \(H_{1/3} = \sqrt{m_0}\).
Summarizing, one can state that the short-term distribution of wave heights, i.e. the wave heights in a stationary sea state exhibits some very characteristic relations:
The maximum individual wave height in a wave record depends on the length of the record. Suppose we have a storm record with a duration of six hours. Suppose the mean wave period is \(\overline{T} = 10s\), so on average we have \(6 \times 60 \times 60/10 \approx 2000\) waves in the record. The maximum individual wave height can now be estimated by setting \(P = 1/2000\) in Eq. \(\ref{eq3.4.4.3}\). We then find that in a storm the maximum individual wave height \(H_{\max} \approx 2H_s\). This is handy method to quickly estimate \(H_s\) from a wave record with a certain number of waves.
| Description | Notation | \(H/\sqrt{m_0}\) | \(H/H_s\) |
| RMS height | \(H_{rms}\) | \(2\sqrt{2}\) | 0.707 |
| Mean height | \(\overline{H}\) | \(\sqrt{2\pi}\) | 0.63 |
| Significant height | \(H_s = H_{1/3}\) | 4.004 | 1 |
| Average of 1/10 highest waves | \(H_{1/10}\) | 5.09 | 1.27 |
| Average of 1/100 highest waves | \(H_{1/100}\) | 6.67 | 1.67 |
For a regular wave, the energy content \(E = 1/2 \rho g a^2 = 1/8 \rho g H^2\). Using Table 3.1 we have for an irregular wave field \(E = \rho g m_0 = 1/8 \rho g H_{rms}^2\). Apparently, the root-mean square wave height \(H_{rms}\) is the wave height representing the total energy content.
In a similar way, wave periods can be determined from the spectral moments. For instance the zero-crossing period:
\[T_2 = \sqrt{\dfrac{m_0}{m_2}}\]
Theoretically this is equal to the zero-crossing period \(\overline{T_0}\) as determined from the time-series. For narrow spectra as for swell, \(T_2\) and \(T_{1/3}\) are approximately equal to the spectral peak period \(T_p\). For a broader spectrum with a high frequency tail (a typical sea spectrum) \(T_{1/3}\) is approximately equal to 0.9-0.95 \(T_p\) and \(T_2\) is roughly equal to 0.7 \(T_p\). However, the value of \(T_2\) should be considered with care; because of the sensitivity of the higher moments for higher frequencies, \(T_2\) will be sensitive to details of the measurements and data-processing.
The wave climate for the North Sea is not very extreme. The significant wave height now and then reaches values of 8 metres in the northern part and 6 metres in the southern part (off the Dutch coast). The mean wave period under those conditions is around 10 seconds. The highest wave in the north is then approximately 15 metre with a period of 15 to 20 seconds. Averaged over the year \(H_s\) = 1m to 1.5m and \(\overline{T}\) = 4 to 5 seconds.
So far we have not taken directionality of the waves into account. In reality however the different harmonic components have different wave directions \(\theta\). That is why you will sometimes also find information on a mean wave direction \(\theta_m\) and the amount of spread around the mean.


