1.6: Processes
- Page ID
- 15510
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Many different processes play important roles in the climate system. In chapter 4 we have already learned about radiation and the global energy budget. Here we want to discuss atmospheric and oceanic circulations, how they transport heat and water, and we’ll explore a little more in depth Earth’s water cycle and how it penetrates all climate system components and is linked to the energy cycle.
a) Atmospheric Circulation
Annual mean surface temperatures on Earth range from less than −40°C in Antarctica to +30°C in the tropics (Figure \(\PageIndex{1}\)). This begs the question: why is it warmer in the tropics than at the poles? The answer is, of course, because there is more sunlight in the tropics.
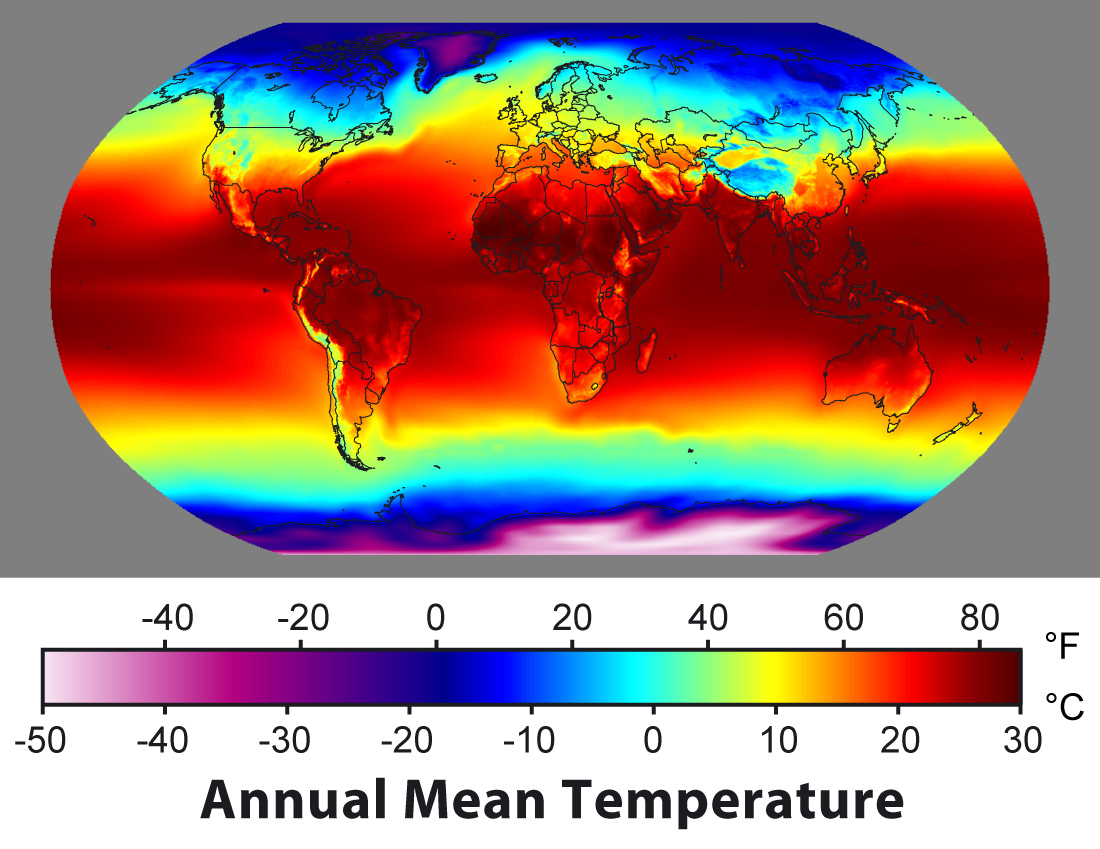
Figure \(\PageIndex{1}\): Annual mean surface temperature distribution. From wikimedia.org.
Due to the curvature of Earth’s surface the equator receives more incident solar radiation per area than the poles (Figure \(\PageIndex{2}\)). Most solar radiation is received on a surface perpendicular to the sun’s rays, whereas the more tilted Earth’s surface is with respect to the sun’s rays the less energy it receives. This is similar to holding a flashlight perpendicular to a surface or at an angle. The area lit is smaller if the flashlight shines perpendicular onto the surface. This configuration maximizes the energy input. The area lit is larger the larger the angle between the flashlight and the surface. In the extreme case of a 90° angle, or more, there is no light at all received. This situation corresponds to the poles or the dark side of the Earth.
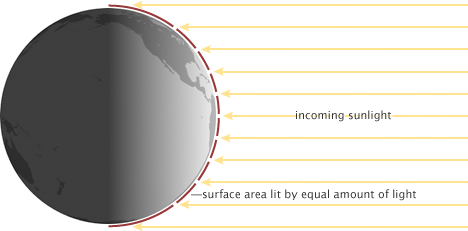
Figure \(\PageIndex{2}\): The amount of incoming sunlight on Earth is spread over a larger area at the poles than at the equator. This leads to less heating of the poles compared to the equator. From earthobservatory.nasa.gov.
Satellites have measured radiative fluxes at the top-of-the-atmosphere. Those data can be used to calculate the heat gain from absorbed solar radiation (ASR) and the heat loss from emitted terrestrial radiation (ETR) as a function of latitude (Fig. \(\PageIndex{3}\)). The data show ASR values of around 300 Wm-2 in the tropics and 60 Wm-2 at the poles. Thus, the equator-to-pole difference is about 240 Wm-2. However, values for the ETR are only around 250 Wm-2 in the tropics and between 150 and 200 Wm-2 at the poles. Thus, the equator-to-pole difference is only about 50 to 100 Wm-2. The difference between the absorbed and emitted radiation gives the net heat gain from these fluxes. In the tropics the gain is positive. That is, there is more energy gain than energy loss. At the poles, on the other hand, there is more energy loss than energy gain. Therefore, if no other processes were involved the equator would warm up and the poles would cool down. But this is not the case, which implies a heat transport from the tropics towards the poles.
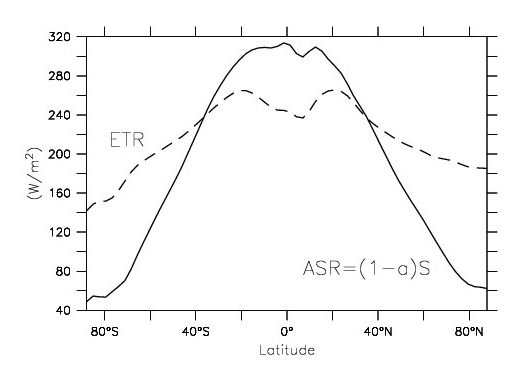
Figure \(\PageIndex{3}\): Absorbed solar radiation (ASR, solid) and emitted terrestrial radiation (ETR, dashed) zonally averaged as a function of latitude from satellite data of Earth’s Radiation Budget Experiment.
Taking the difference ASR – ETR and integrating it from one pole to the other gives the total meridional heat flux (Figure \(\PageIndex{4}\)). In the southern hemisphere values are negative indicating southward heat transport. Positive values in the northern hemisphere represent northward transport. Poleward heat fluxes are peak at mid-latitudes with values of between 5 and 6 PW.
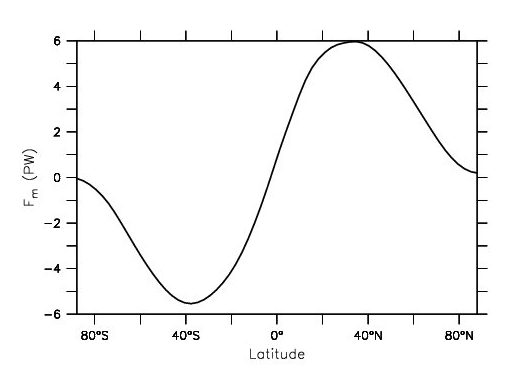
Figure \(\PageIndex{4}\): Meridional (northward is positive) heat transport in the climate system as a function of latitude implied from integration of the differences in the fluxes shown in Figure \(\PageIndex{3}\). Units are peta watts (1 PW = 1015 W).
Most of the meridional heat transport is carried by the atmosphere (4-5 PW) whereas the ocean is responsible for a smaller portion (1-2 PW). Complex and turbulent motions in the atmosphere such as seen in visualizations from satellites play an important part in this heat transfer.
Air is compressible. The weight of overlaying air compresses the air beneath and increases the pressure closer to the surface (Figure \(\PageIndex{5}\)). Therefore, pressure decreases with height and the surface pressure depends on the density and mass of the air above.
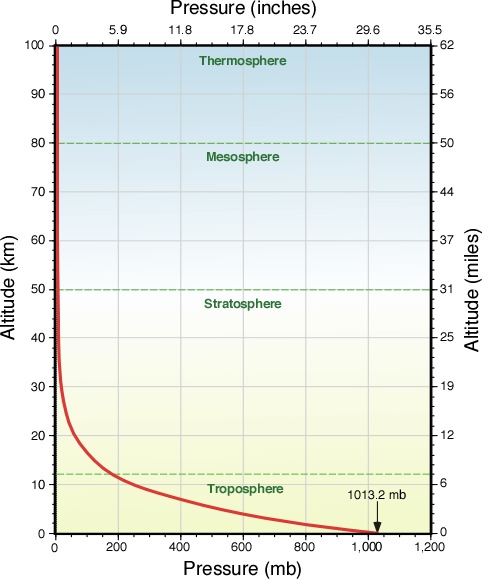
Figure \(\PageIndex{5}\): Air Pressure as a Function of Altitude. From physicalgeography.net.
Let’s imagine a non-rotating Earth (Figure \(\PageIndex{6}\)). In this case, the air at the poles would be cold and the air at the equator would be hot. Since colder air is denser than warm air the pressure at the north pole would be larger than at the equator. The air at the equator would rise and the air at the poles would sink. At the surface, the air would flow from high to low pressure, thus from the poles to the equator. At high altitudes the air would move from the equator to the poles.
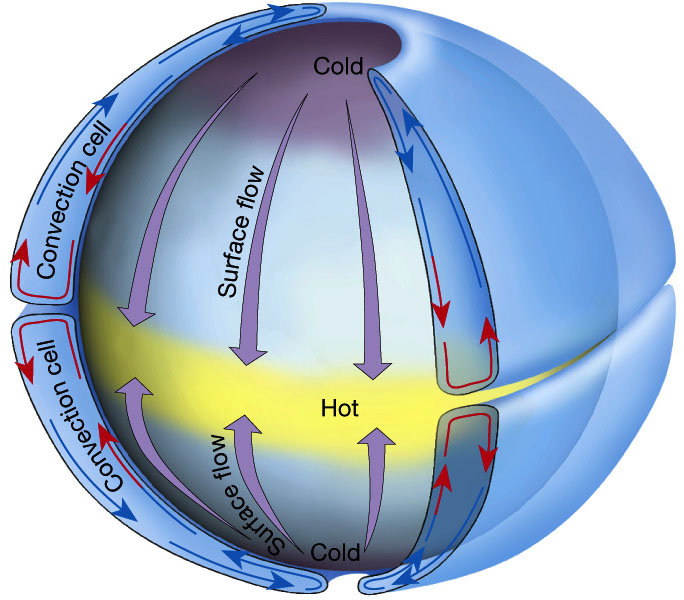
Figure \(\PageIndex{6}\): Atmospheric Circulation on a Non-Rotating Earth. Figure 7.5 in The Atmosphere, 8th edition, Lutgens and Tarbuck, 8th edition, 2001. From ux1.eiu.edu.
However, Earth does rotate, which creates the Coriolis effect. Earth’s rotation causes a deflection of air and water masses towards the right (left) in the northern (southern) hemisphere. The Coriolis force is a consequence of angular momentum conservation. Assume an air parcel at rest at the equator. (An analogy would be a spinning ice dancer with extended arms.) Its angular momentum is M = R×U, where U = 40,000 km/day = 500 m/s is approximately the velocity of the Earth at the equator. Now move the air northward. (The ice dancer pulls his/her arms in.) This will decrease R. In order to conserve angular momentum U has to increase. If the air moved to about 60°N its distance from the axis of rotation would have decreased by about one half. Therefore, U must have doubled. Thus, the air parcel would have a velocity of 500 m/s relative to the Earth’s surface. Such high speeds never occur on Earth because of friction and turbulence but this simple example still explains qualitatively the high eastward wind velocities of around 40 m/s observed in the mid-latitude jet streams (Figure \(\PageIndex{7}\)).
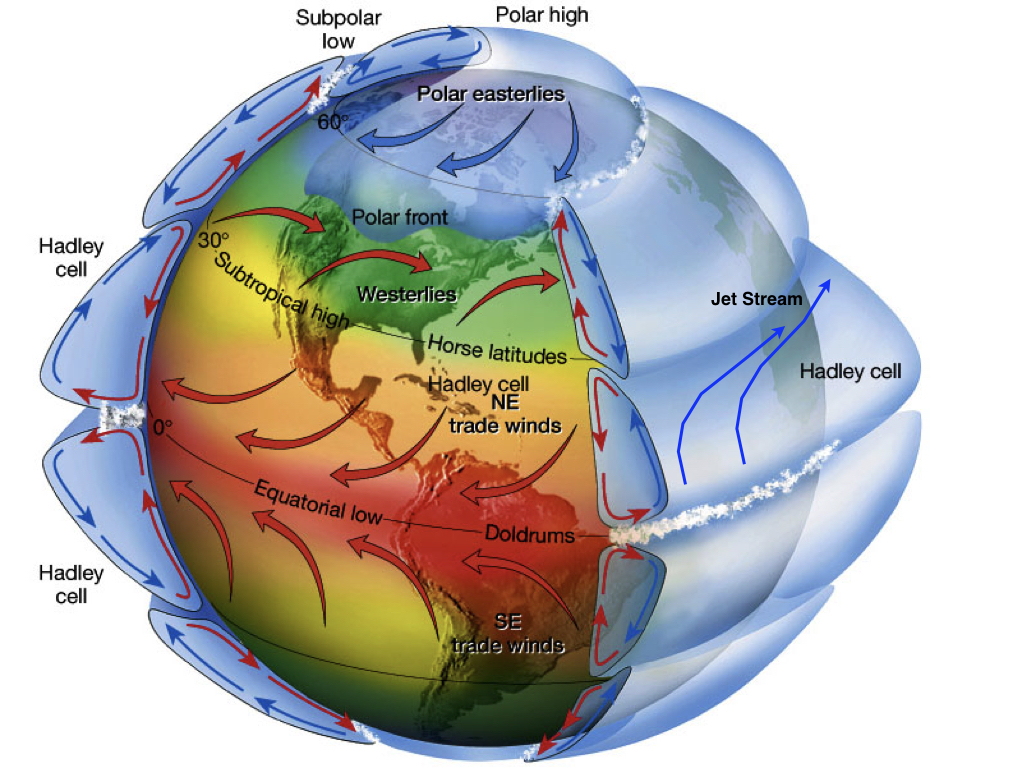
Figure \(\PageIndex{7}\): Atmospheric Circulation on a Rotating Earth. Modified from ux1.eiu.edu.
Rising of warm moist air at the equator causes water vapor condensation due to cooling of the air during the ascent. Clouds form and precipitation occurs. Some of the deepest cumulonimbus clouds on Earth form in the tropics. They can reach the top of the troposphere or higher. The cool relatively dry air then moves poleward. Now the Coriolis effect kicks in, deflects the air towards the right (left) in the northern (southern) hemisphere, which creates the jet stream. The air cools by emitting longwave radiation to space. This increases the density and the air descends back to the surface in the subtropics (~30°N/S). During the descend the air warms and its relative humidity decreases. This leads to dry conditions in the subtropics indicated by the major deserts at those latitudes.
Subsequently the dry air moves back towards the equator. The Coriolis force deflects it towards the right (left) in the northern (southern) hemisphere, creating the easterly trade winds in the tropics. During this movement along the sea surface the air picks up water vapor from evaporation. Once the air returns to the equator it is saturated with water vapor (close to 100% relative humidity). The resulting meridional overturning cells in the tropical atmosphere are called Hadley cells, or Hadley circulation. Two cells, one in each hemisphere, exist only during the fall and spring, whereas during summer/winter there is only one major cell with rising air just slightly off the equator in the summer hemisphere, where the heating is largest.
The belt of rising air close to the equator is called the Intertropical Convergence Zone (ITCZ), due to the convergence of air along the surface. The ITCZ is further north in the northern hemisphere summer and further south in the southern hemisphere summer, although on average it is slightly north of the equator because the northern hemisphere is slightly warmer than the southern hemisphere due to ocean heat transport from the southern to the northern hemisphere (Frierson et al., 2013).
Water in the Hadley Cell
Let’s follow an air parcel of about 1 kg weight (~1 m3 at the surface) during its travels along the Hadley cell and estimate its water vapor content using Fig. 16 of chapter 4.
- Starting at the ITCZ we assume the temperature is 30°C and the air is fully saturated with water vapor. How many grams of water vapor does it contain?
- The air ascends to the top of the troposphere. It cools to about -30°C. It is still at saturation. How many grams of water vapor does it contain?
- How many grams of water vapor has the air parcel lost?
- Now the air parcel moves poleward and descends in the subtropics. The descend causes warming. Will the water vapor content change during the descend?
- Let’s assume the surface temperature is close to 30°C. What will be the relative humidity of the air?
- During its travels near the surface evaporation from the ocean will quickly increase the air parcel’s water vapor content close to saturation. How many grams of water vapor will the air parcel have gained?
Surface air moving from the high pressure at subtropical latitudes towards lower pressure at mid-latitudes also experiences the Coriolis effect. This leads to the prevailing westerly winds at mid-latitudes. Another important feature of the atmospheric circulation at mid-latitudes is the growth, movement, and decay of synoptic weather systems (transient eddies) that dominate weather variability and heat transport there. Transient eddies are the low and high pressure systems that move eastward, some of which can be associated with storms.
Explore these features of the global atmospheric circulation in this animation of weather variations throughout a whole year from satellite observations.
You may notice the pulsing of convection over tropical Africa and South America. This is caused by the diurnal (daily) cycle of surface heating. Fig. \(\PageIndex{8}\) shows the observed global distribution of precipitation. Note the ITCZ as the band of high precipitation close to the equator, the regions of low precipitation in the subtropics and the bands of high precipitation at mid-latitudes in the paths of the storm tracks over the North Pacific and North Atlantic. In the southern hemisphere we see an additional band between 50-60°S.
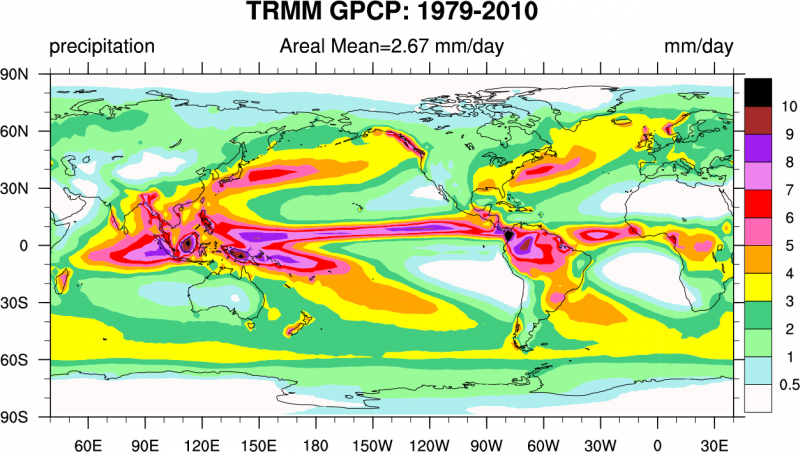
Figure \(\PageIndex{8}\): Annual mean precipitation estimated from observations. From ucar.edu.
Precipitation has a strong effect on vegetation as can be seen from the similarities between Figures \(\PageIndex{8}\) and \(\PageIndex{9}\). Regions of large precipitation such as tropical Africa, South America, and Asia have dense vegetation, whereas regions of little precipitation such as the Sahara, the Arabian Peninsula, regions in central Asia, southwestern parts of North America, central and western Australia, parts of South America west of the Andes, and southwestern Africa also have sparse desert or steppe vegetation. This relation is not a surprise considering that photosynthesis requires water (see box Photosynthesis and Respiration in the Chapter on Carbon).
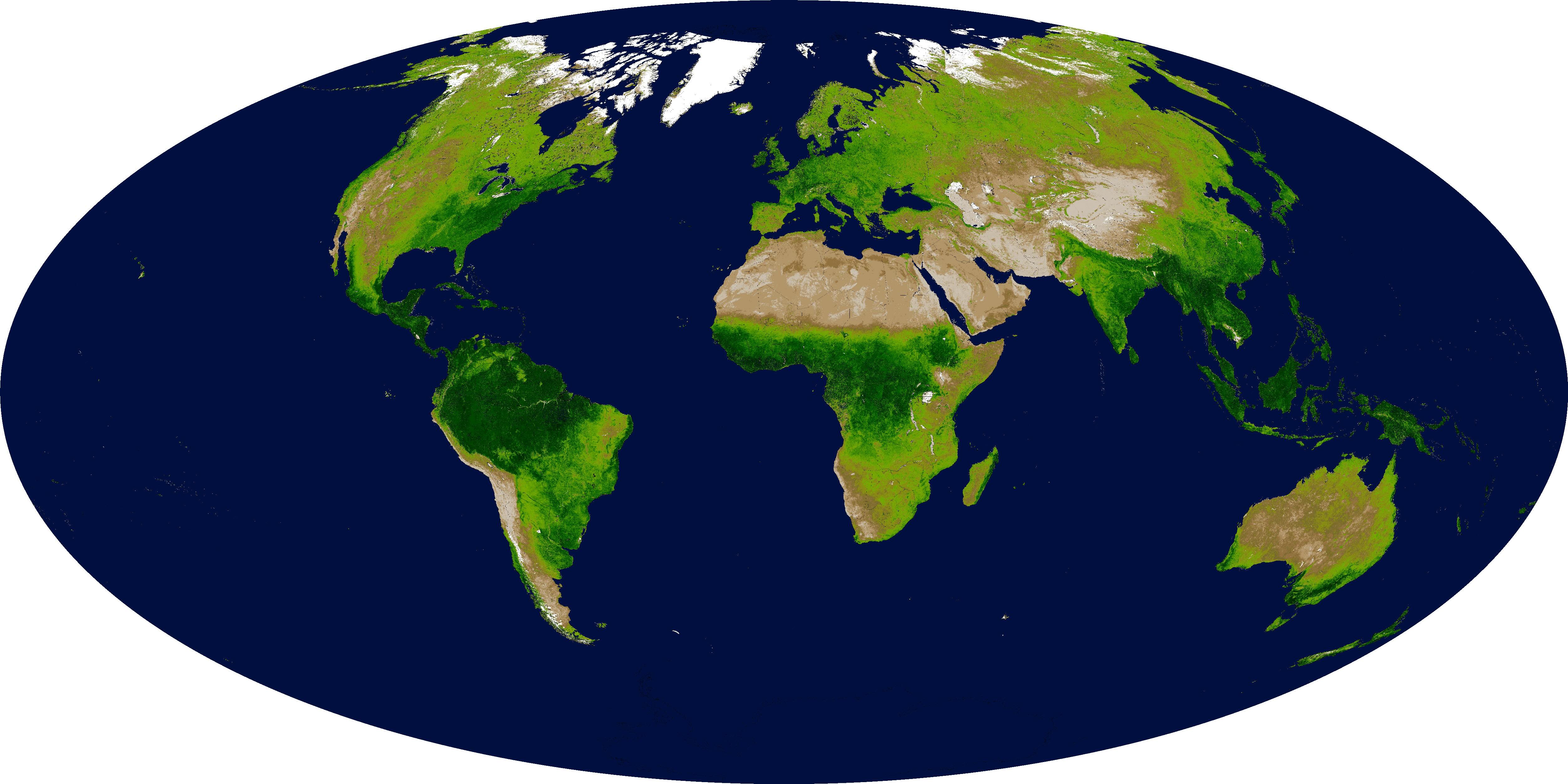
Figure \(\PageIndex{9}\): Global Vegetation Distribution From Satellites. Shown is the Enhanced Vegetation Index (EVI), which represents the concentration of green leaf vegetation. From nasa.gov.
b) The Hydrologic Cycle
Water plays a fundamental role in the climate system. It is involved in Earth’s energy cycle and links physical and biological processes. Water has some remarkable properties due to its molecular structure. Hydrogen bonds in liquid water result from attractive electric forces between the positively charged hydrogen atoms of one molecule with the negatively charged oxygen atom of a neighboring molecule. A large amount of energy input is required to overcome this force for a transition from the liquid to the vapor phase (Fig. \(\PageIndex{10}\)). This energy is called latent heat of vaporization. It is about 2,300 joules per gram of water. The same amount of energy is released during condensation.
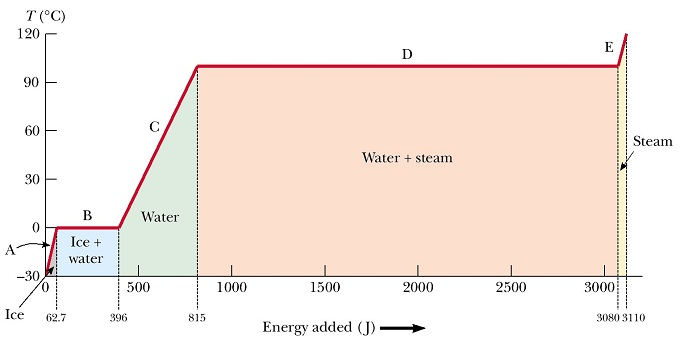
Figure \(\PageIndex{10}\): Effects of heat added (ΔH) on the temperature of one gram of water. Starting from ice at -30°C we need to add about 63 J to warm it up to the melting point (line A). About 333 J are required to melt the ice (line B). During this process the temperature stays constant. Once all ice is melted into water adding more heat causes the water temperature to increase until the boiling point (line C). The slope of line C is the heat capacity of water (at constant pressure) cp,water = ΔH/ΔT = 4.2 J/(g°C). Once the water boils any added heat is used to vaporize water and the temperature stays at the boiling point until all water is vaporized. The latent heat of vaporization is ~2270 J/g. Thus, the energy required to vaporize water is more than five times as much as to warm it from 0°C to 100°C.
Lapse Rate
The lapse rate Γ = ΔT/Δz is the rate of temperature decrease ΔT with height Δz in the atmosphere. Let’s try to estimate the effect of condensation of water vapor in the ascending branch of the Hadley cell on the temperature of the upper atmosphere (z = 10 km). In the previous box we have calculated that approximately 30 g of water vapor were lost from 1 kg of air during its ascent.
- How much latent heat of condensation was released?
- How much would that added heat have increased the temperature of the air parcel, assuming a specific heat capacity of air of cp,air = 1 J/(g°C)?
The observed lapse rate of the atmosphere is on average about Γm = -6.5 °C/km, which is close to the moist adiabatic lapse rate. (Adiabatic means that no heat is added or removed from the air parcel.) This is in contrast to the dry adiabatic lapse rate, which is approximately Γd = -10 °C/km. Thus, given a surface air temperature of 30°C, the air at 10 km altitude at the equator would be -70°C in a dry atmosphere compared with -35°C in the real, moist atmosphere. Our calculation above was not quite correct due to the various assumptions we made, but the order of magnitude was right. This example illustrates the large effect of latent heat release on upper air temperatures.
Condensation occurs when the air is at 100% relative humidity and when cloud condensation nuclei are available. Cloud condensation nuclei are small particles in the air. In the atmosphere condensation typically occurs when the air is cooled, e.g. during ascending motions in convection or when air is lifted over mountains. The latent heat released during condensation in clouds leads to warming and thus more intense upward motions. This is an important driver of convection and storms (Fig. \(\PageIndex{11}\)).

Figure \(\PageIndex{11}\): Picture of a convective cloud. Warming from latent heat release during condensation makes the interior of a cloud more buoyant than the surrounding air and thus intensifies convection. From globalwaterforum.org.
Evaporation occurs when the relative humidity rh = q/qsat of the air above a water surface is less than 100%. q is the specific humidity, that is the amount of water vapor (in grams) per moist air (in kg) and qsat is the specific humidity at saturation. The lower the relative humidity the higher the rate of evaporation E ~ qsat – q. Stronger winds also cause more evaporation, similar to your blowing over your hot coffee or tea to cool it down. Evaporation leads to cooling of the remaining liquid water since it removes the fastest molecules, and the slower ones stay behind. This principle is also at work in air conditioners and refrigerators, in which air is cooled by evaporation of a coolant. Evaporative cooling is important in keeping Earth’s surface and especially the ocean cool. Over vegetated land areas transpiration of water by plants also cools the surface. Plants can limit their water loss through transpiration by closing their stomata.
Another property of water that is important for climate is its large heat capacity. The table below compares the heat capacity of water with that of air. On a per gram basis water already has more than four times the heat capacity of air. Moreover, the density of water is 1000 times that of air. Therefore, on a per volume basis the heat capacity of water is 4200 times that of air. As a result, the top 2 m of the ocean has the same heat capacity as the whole atmosphere.
| Units | Air | Water | ||
| Specific Heat Capacity | cp | J/(g°C) | 1 | 4.2 |
| Density | ρ | kg/m3 | 1 | 1000 |
| Volumetric Heat Capacity | cvol = cpρ | J/(m3°C) | 1000 | 4,200,000 |
Note
The differences in heat capacity of air versus water can be demonstrated in a simple experiment with two balloons. You can do this at home. Fill one balloon with with air, the other with water. We will hold the flame of a lighter to the balloon.But first make a guess what will happen. Will there be a difference in the results?
- Now perform the experiment with the air balloon first. What happened?
- Now perform the experiment with the water balloon. Is there a difference?
- Did you expect these results?
If you don’t want to do the experiment yourself you can watch a video here.
Experiment: Heat Capacity
The differences in heat capacity of air versus water can be demonstrated in a simple experiment with two balloons. You can do this at home. Fill one balloon with with air, the other with water. We will hold the flame of a lighter to the balloon.
- But first make a guess what will happen. Will there be a difference in the results?
- Now perform the experiment with the air balloon first. What happened?
- Now perform the experiment with the water balloon. Is there a difference?
- Did you expect these results?
If you don’t want to do the experiment yourself you can watch a video here.
Land also has a much lower heat capacity than the ocean. Let’s consider the budget equation for two cases: an air column with ocean and one with land. Let’s also assume the system was initially in balance, e.g. ΔCT/Δt = I – O = 0 (zero), which means the rate of change in heat content CT is zero and thus the temperature T is constant. C is the heat capacity, which is larger for the column with the ocean underneath. Now, we add a forcing ΔF on the right-hand-side such that ΔCT/Δt = ΔF. Because the heat capacity is a constant (it does not change with time) we can divide by C to get the temperature change ΔT/Δt = ΔF/C. This equation implies that the temperature change over the ocean will be slower than over land because it has a larger heat capacity C.
The effects of the differences in heat capacity between the ocean and land can be seen in Fig. \(\PageIndex{12}\), which shows the amplitude of the seasonal cycle in surface temperatures (summer minus winter). The seasonal cycle in the forcing is much larger at higher latitudes than in the tropics, which explains why the seasonal temperature variations in the tropics are smaller than at higher latitudes. But you also see a larger difference between the seasonal cycle over land and over the ocean at similar latitudes. E.g. over the North Pacific at 40°N temperatures in summer are only about 10°C warmer than in winter, whereas in the interior of North America they are 30°C warmer. The largest amplitudes of the seasonal cycle are over east Siberia, because it is the furthest downstream from the ocean (remember the prevailing westerly winds at those latitudes) and over Antarctica because it is, for dynamic and topographic reasons, isolated. Dynamically the large westerly winds over the Southern Ocean inhibit meridional transport. Topographically, the sheer height of the ice sheet removes it from what is happening at the sea surface.
In the data explorations in the Weather Chapter you may have found similar features such as a smaller seasonal cycle closer to the ocean than in the continental interior. Most people live close to the ocean presumably at least partly because climate variations there are more dampened and less extreme than in the interior of the continents
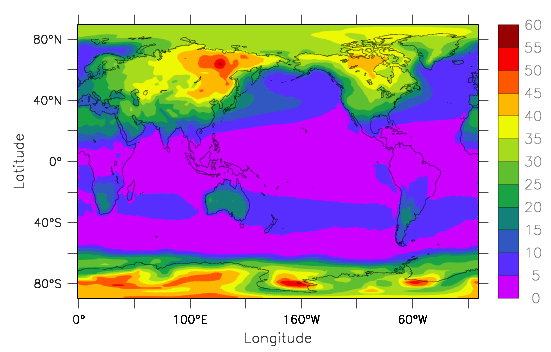
Figure \(\PageIndex{12}\): Amplitude of the Seasonal Cycle of Surface Temperatures. Plotted is the maximum minus the minimum of the average seasonal cycle from 1958 to 1996 from the National Center for Environmental Prediction (NCEP) Reanalysis. Units are in degrees Celsius.
The large heat capacity of the ocean not only dampens seasonal temperature variations but also those on other timescales. We have seen in Chapter 2 that observed warming over the past 100 years is also smaller over the ocean than over land. Now we understand that the observed land-sea contrast is due, at least in part, to the differences in heat capacities.
In fact, about 90% of the observed increase in Earth’s heat content goes into the ocean (Figure \(\PageIndex{13}\)). Most of the remaining 10% goes into ice and land, whereas the heat gain of the atmosphere is very small in comparison.
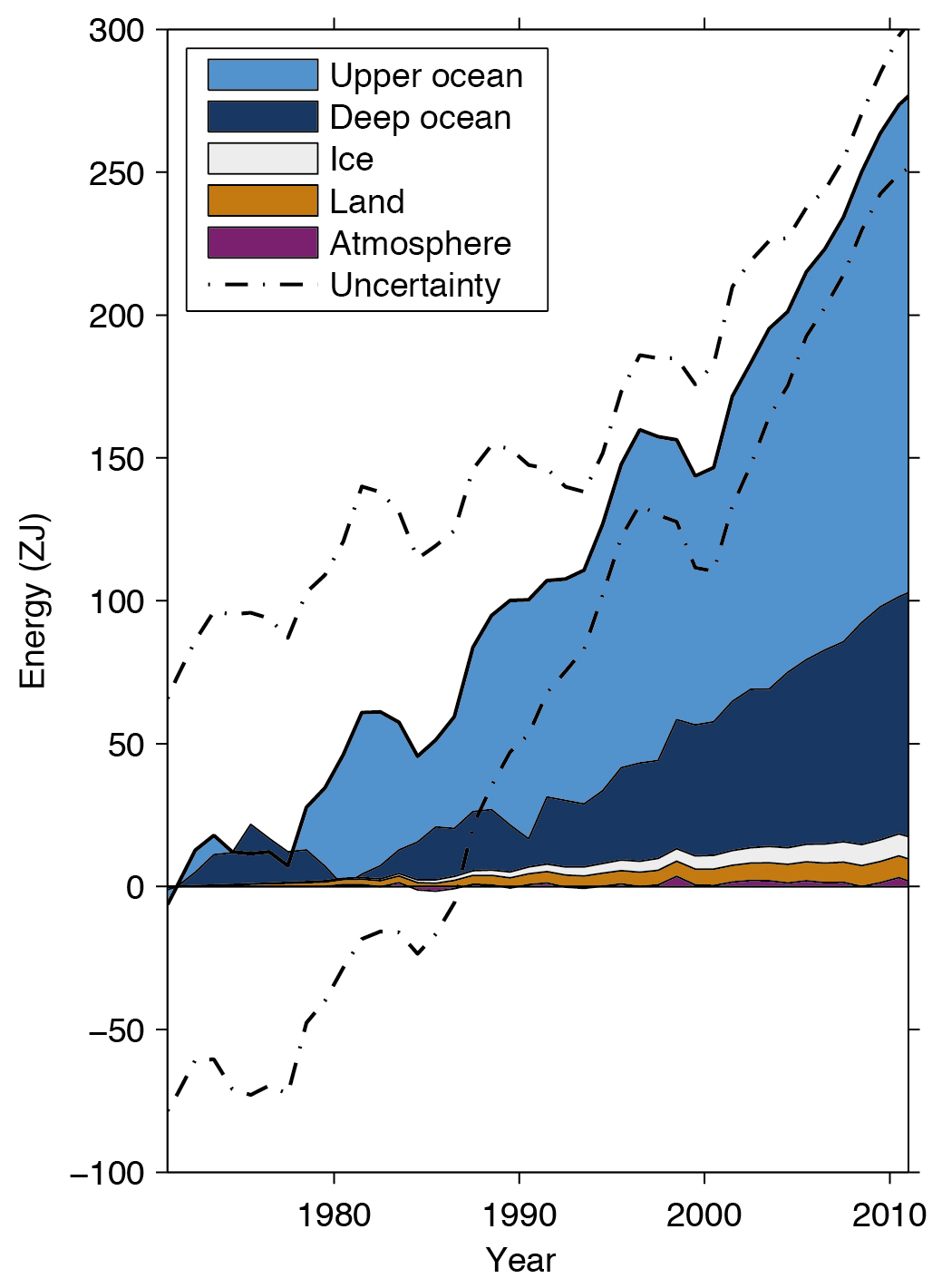
Figure \(\PageIndex{13}\): Changes in Earth’s Heat Content.
Fig. (\(\PageIndex{14}\)) shows a schematic of the global water cycle. Most water is contained in the ocean (more than one billion cubic km), whereas the atmosphere contains only a relatively small amount (13 thousand cubic km). Evaporation removes about 400 thousand cubic km from the ocean each year, most of which precipitates back over the ocean. 40 thousand cubic km are transported in the atmosphere from the ocean to land each year. Over land this water precipitates together with about 70 thousand cubic kilometers of recycled water from evapotranspiration from land surfaces.
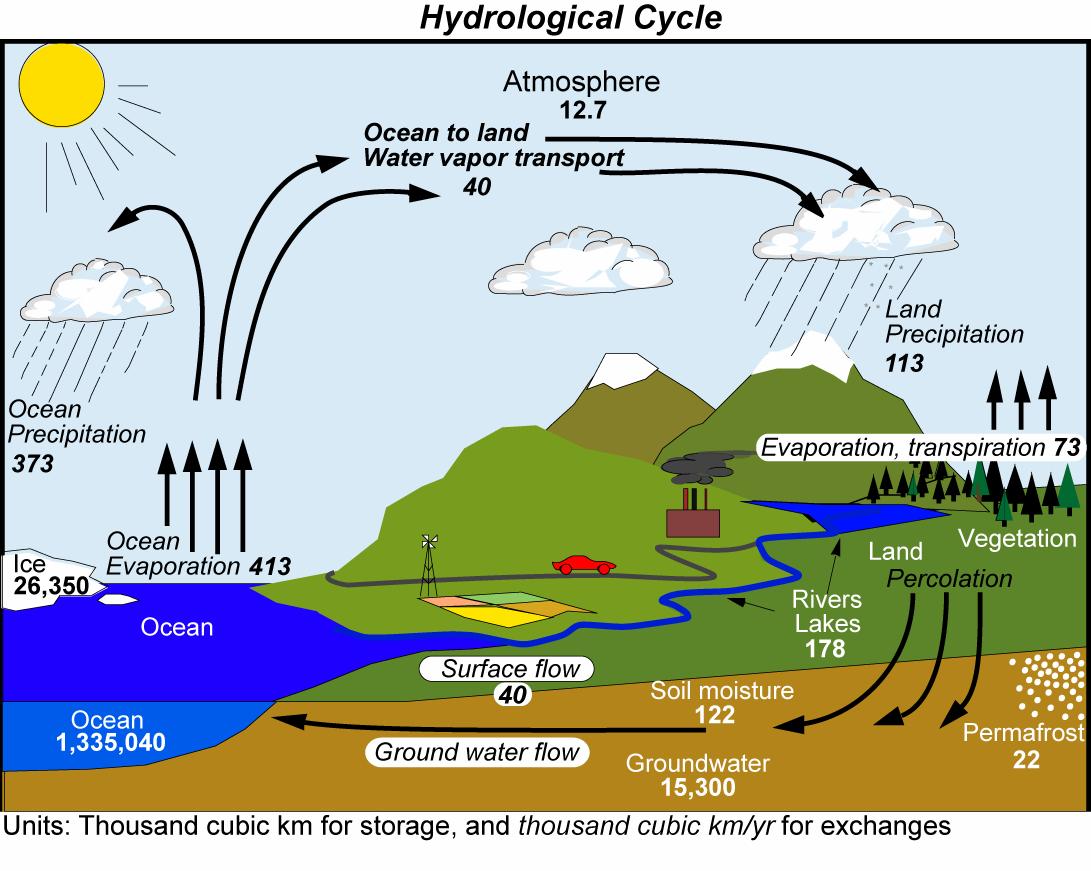
Figure \(\PageIndex{14}\): The Global Water Cycle. Fluxes are indicated in slanted font. From Trenberth et al. (2007). Image from ucar.edu.
Observations show increases in water vapor content in the atmosphere (Figure \(\PageIndex{15}\):). This is consistent with our understanding of the physics of the hydrologic cycle and its dependency on temperature (Clausius-Clapeyron relation). Warmer air can hold more water vapor, and due to the presence of the oceans there is no lack of water supply to the global atmosphere.
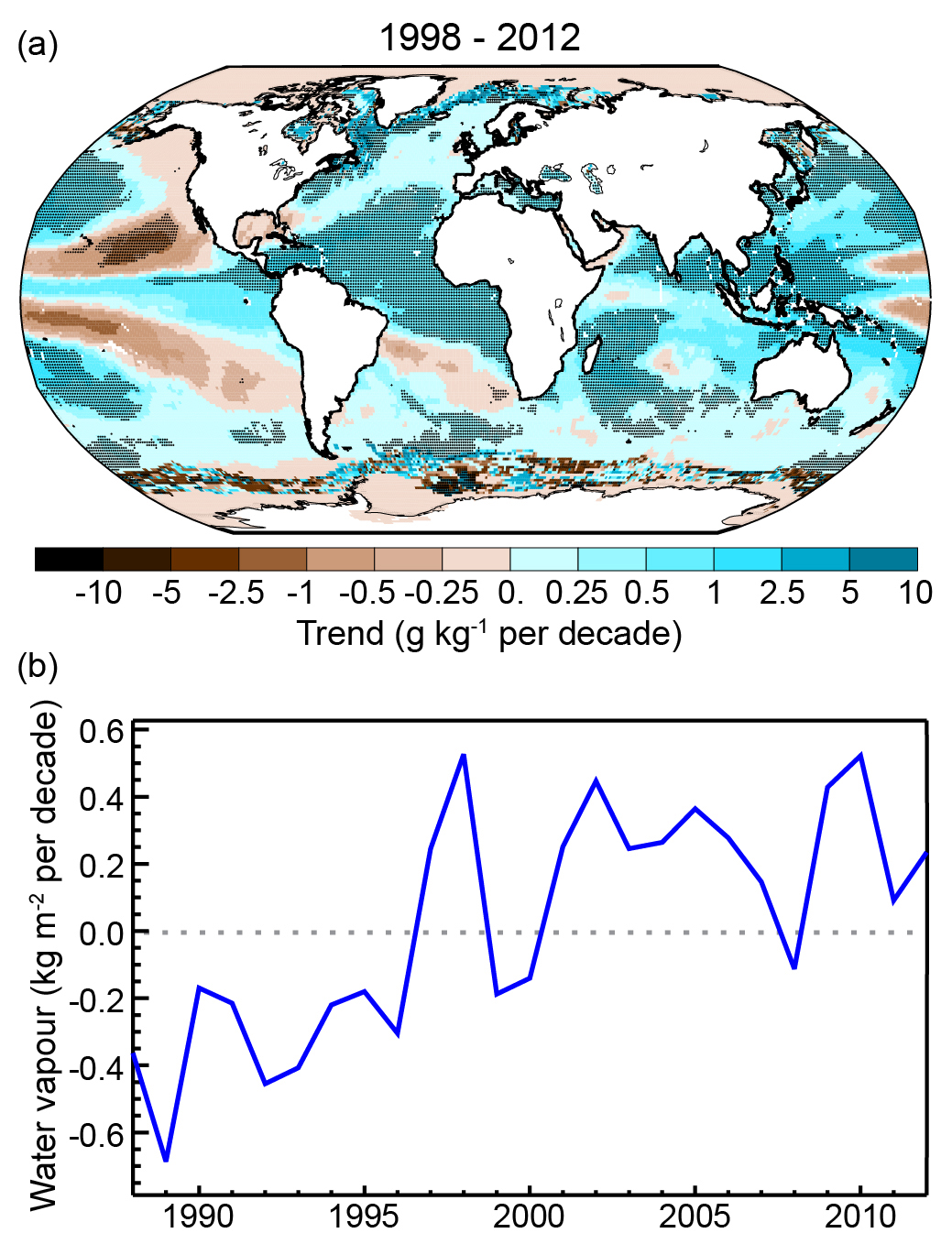
Figure \(\PageIndex{15}\): (a) Observed changes in surface specific humidity estimated from satellites. Dark shading indicates significant changes. (b) Changes in globally averaged water vapor content. From Harmann et al. (2013). Image from ipcc.ch.
c) Ocean Circulation
The general, planetary-scale circulation of the ocean can be separated into a wind-driven component that dominates the upper ocean and a density driven component that occupies the deep ocean. Five large gyres are the main features of the surface circulation in the subtropics (Fig. \(\PageIndex{16}\). The easterly trade winds push water towards the west in the tropics. The water piles up where it encounters land and flows poleward. The poleward flow brings warm waters from the tropics to the mid-latitudes. There, the westerly winds push the surface waters toward the east. Again, where the current hits a continent it piles up and flows north and south. The southward flowing part completes the subtropical gyre bringing cold waters towards the tropics. The poleward flow along the western boundaries of the subtropical gyres are warm currents, such as the Gulf Stream, the Kuroshio, and the Brazil Currents. Equatorward currents along the eastern boundaries are cold such as the California or the Peru (or Humboldt) Currents. Within the subtropical gyres the water flows in a spiral-like pattern towards the center of the gyre. This convergence causes sinking in the centers of the gyres. However, the water is relatively warm so it sinks only to depths of a few hundred meters. In the tropics, on the other hand, the trade winds cause divergence and upwelling.
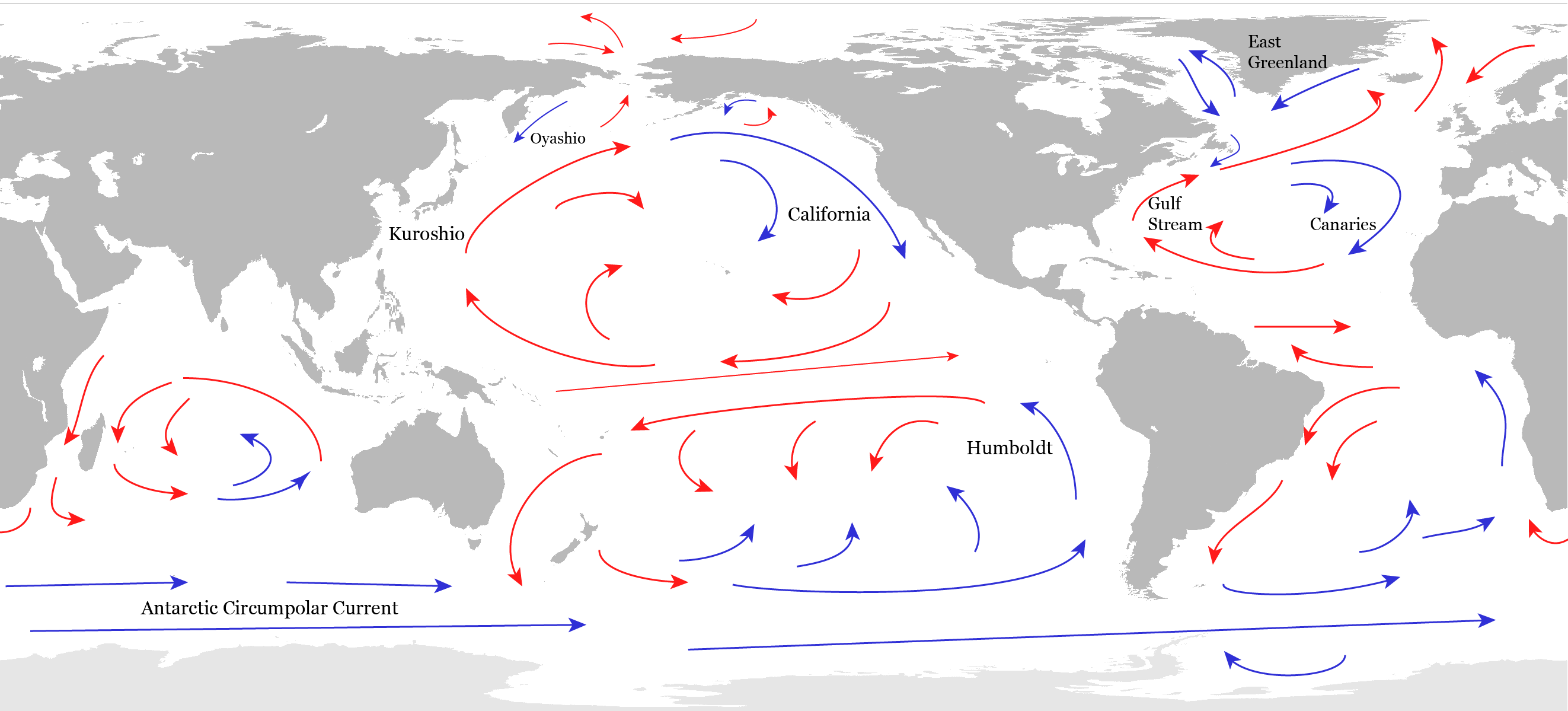
Figure \(\PageIndex{16}\): Sketch of the Surface Circulation of the Ocean. After Peixoto and Oort (1992).
Surface currents near the equator are particularly vigorous. The piling up of waters in the western equatorial Pacific, for example, causes the narrow Equatorial Counter Current to move eastward.
The strongest current in the world oceans is the Antarctic Circumpolar Current, which transports more than 100 million cubic meters of water per second around Antarctica flowing eastward. That amounts to 500 times the Amazon river discharge. The Southern Ocean is also an important region for upwelling of deep waters caused by a wind-driven divergence of surface waters.
Watch a high resolution model simulation of surface ocean currents here.
It shows more details such as mesoscale eddies, which are the ocean’s equivalent of weather systems in the atmosphere. Notice that they are much smaller in size than high and low pressure systems in the atmosphere due to the larger density of seawater compared with air. Try to identify some of the features discussed above such as the Gulf Stream and the Antarctic Circumpolar Current. These and other fascinating features are also seen in satellite observations of sea surface temperatures here
and here.
In contrast to the atmosphere, the ocean is mostly stably stratified. That is, denser water is layered below lighter water. The density of sea water is determined by temperature and salinity. The colder and saltier, the heavier it is. Typically warmer, more buoyant water is on top of colder water, especially at low latitudes (Fig. \(\PageIndex{17}\)). This is because water absorbs sunlight efficiently, which heats the surface. Winds cause lots of turbulence close to the surface, which creates a layer of uniform temperature called the surface mixed layer. Below that, between about 200 – 1000 m depth, is a region in which the temperature decreases rapidly with depth. This is called the thermocline. Turbulence is weak here. Further down is the weakly stratified deep and abyssal ocean. Vertical temperature gradients are small here. Closer to the sea floor turbulence increases due to interactions of flow with the bottom topography.
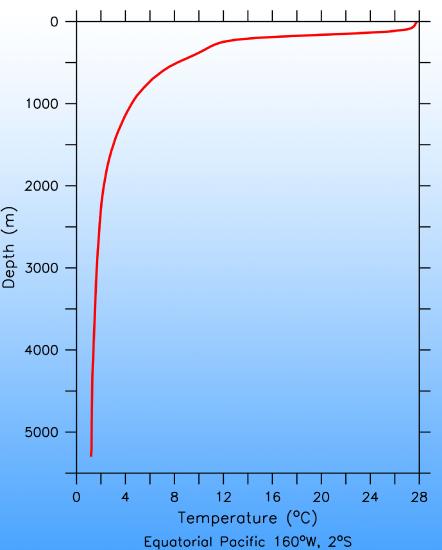
Figure \(\PageIndex{17}\): Typical Temperature Profile with Depth in the Ocean.
The deep ocean is cold because waters there originate from the high-latitude surface. Only in a few regions of the world’s oceans where the density of surface waters is large enough do they sink into the deep ocean (Fig. \(\PageIndex{18}\)). In the current ocean there is deep water formation in the North Atlantic and near Antarctica. Surface waters of the Atlantic are saltier than those of the Pacific because of water vapor transport within the atmosphere. Whereas mountain ranges at mid-latitudes block water vapor transport from the Pacific to the Atlantic with the westerly winds there, in the tropics gaps in the mountains allow water vapor transport with the trade winds from the Atlantic to the Pacific. This causes fresher, more buoyant surface waters in the Pacific. In the North Pacific this freshwater lens prevents sinking, whereas in the North Atlantic saltier waters are dense enough to sink to about 2-3 km depth. From there they flow south along the margin of the Americas pushed there by the Coriolis force. The deep water from the North Atlantic crosses the equator and the South Atlantic and enters into the Southern Ocean. Part of it rises back to the surface there whereas the rest flows into the Indian and Pacific Oceans, where it slowly ascends. The return flow at the surface flows through the Indonesian Archipelago into the Indian Ocean, merges with upwelled waters there and continues to flow westward around the tip of South Africa and back northward across the Atlantic. This planetary scale circulation pattern is called the thermohaline (thermo = temperature, haline = salinity) circulation or meridional (north-south) overturning circulation.
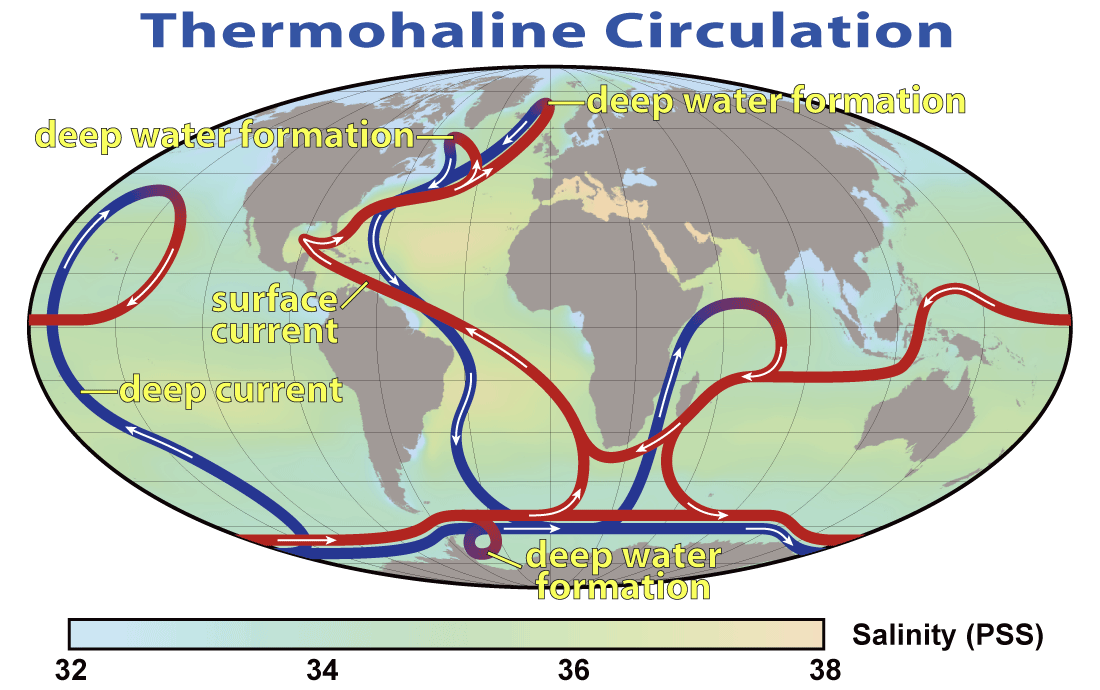
Figure \(\PageIndex{18}\): Cartoon of the Deep Ocean Circulation. Red and blue ribbons represent surface and deep currents, respectively. From Wikipedia.org.
Its circulation impacts tracer distributions in the ocean (Figure \(\PageIndex{19}\)). E.g. in the Atlantic the southward flowing North Atlantic Deep Water (NADW) can be identified as a water mass with relatively high salinity between about 2 – 4 km depth. Fresher Antarctic Bottom Water (AABW) flows north below NADW. It is colder and therefore denser than NADW. Relatively fresh Antarctic Intermediate Water (AAIW) flows north above NADW creating a sandwich-like structure in the deep Atlantic. In the North Atlantic there is a blob of high salinity water around 1 km depth and 40°N. This is outflow from the Mediterranean Sea, which is very salty.
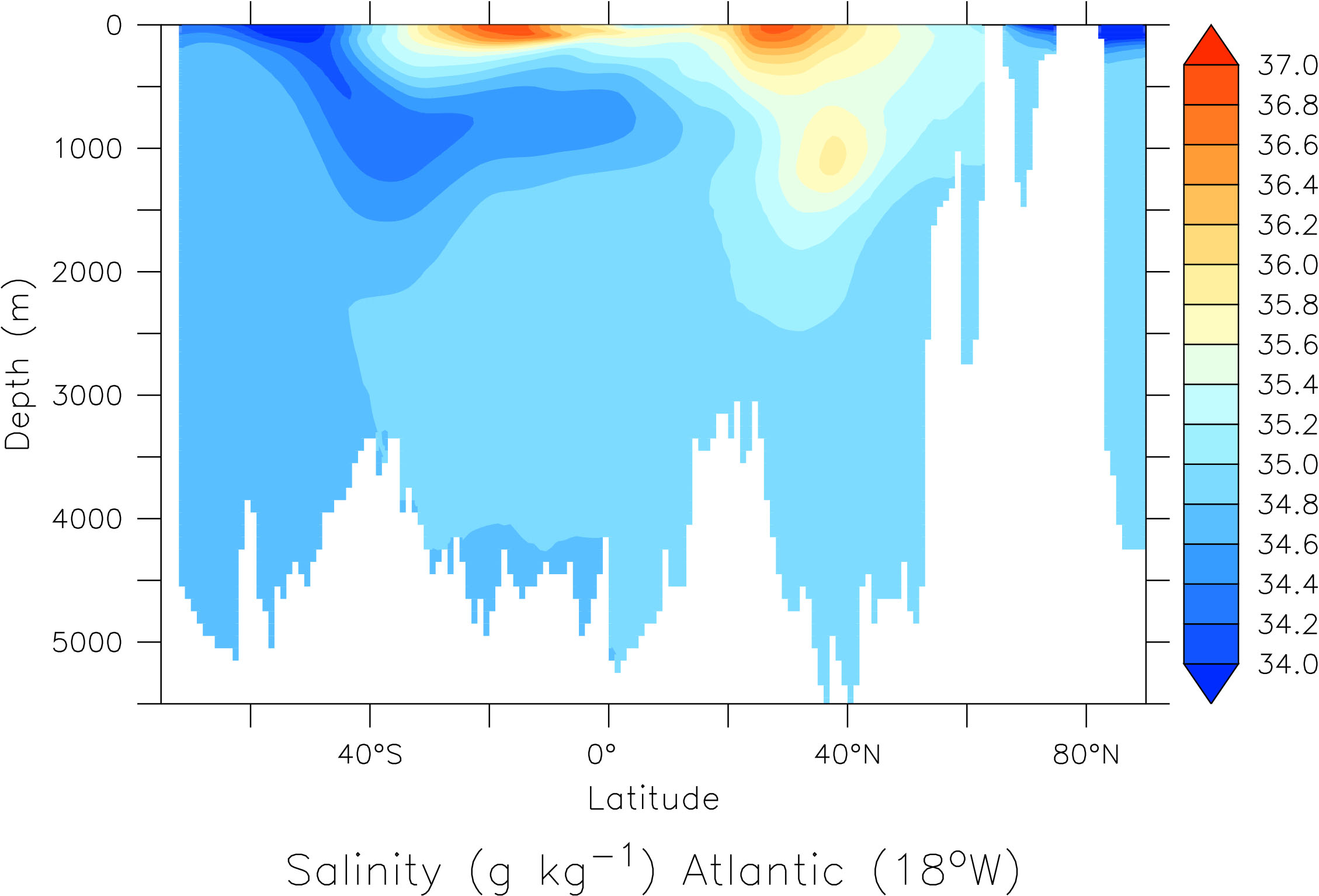
Figure \(\PageIndex{19}\): Salinity (in grams salt per kg of sea water) section through the Atlantic ocean at 18°W as a function of latitude and depth.
Experimet Thermohaline Circulation
Perform a simple experiment that illustrates the effects of salinity and temperature on the density of water. You’ll need the following ingredients:
- a container, preferably made out of a transparent material such as glass or plexiglass,
- ice cubes,
- a small sponge, and
- food coloring.
Fill the container with water. Now put the moist sponge at the surface of the water so that it swims on the top. Pour some salt on the sponge. Not too much. You don’t want it to spill over or capsize the sponge. Just enough so that the water in contact with the sponge will soak up the salt. Now add a few drops of food coloring on top of the salty sponge and observe what happens. Where does the water flow?
Now add an ice cube to the water. Drip a few drops of food coloring (choose a different color than before) onto the ice cube and observe. What happens? Describe your observations. Explain your observations with what you’ve learned about the effects of salinity and temperature on sea water density.
Observations show that the ocean is warming (Fig. \(\PageIndex{20}\)). Most of the increase in temperatures is concentrated near the surface consistent with a warming atmosphere as its cause. A prominent maximum of heat uptake is in the North Atlantic, similar to the pattern of anthropogenic carbon uptake (See this figure). The reason is the sinking and southward penetration of NADW, which transports both anthropogenic carbon and heat from the surface to the deep ocean there. Other regions of enhanced heat uptake are the subtropics, where surface waters sink to a few hundred meters depth in the centers of the subtropical gyres. Ocean temperature observations rule out that changes in ocean circulation are the cause of the observed warming of the surface. If this was the case deeper layers would have cooled, which is not what is observed. Therefore, the hypothesis that changes in ocean circulation have caused the observed warming of the atmosphere during the past 50 years has been falsified by subsurface temperature observations.
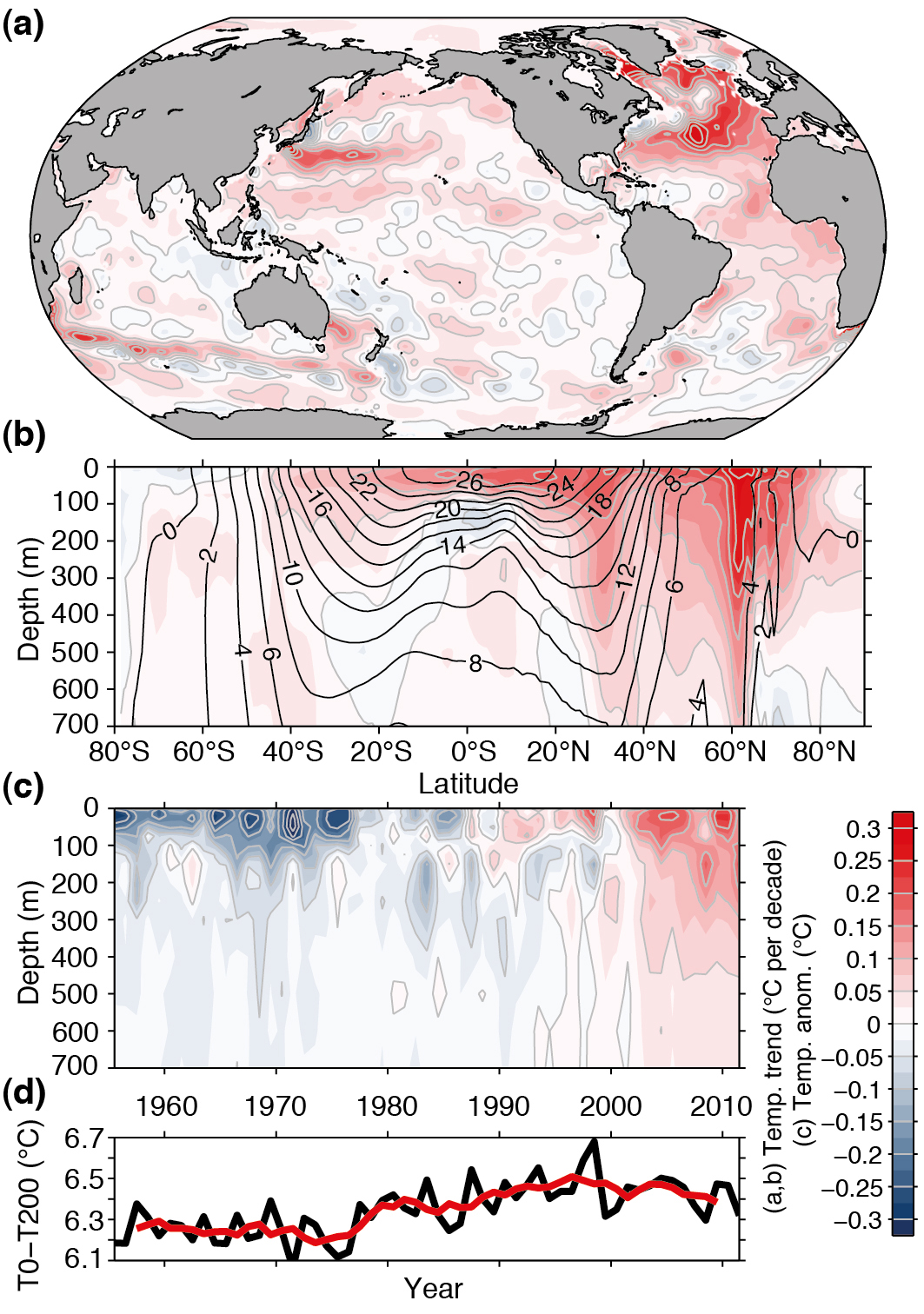
Figure \(\PageIndex{20}\): (a) Temperature trend over the top 700 m from 1971-2010. (b) Zonally averaged temperature trend. Black contour lines represent the mean temperature distribution. (c) Horizontally averaged temperature changes. (d) Changes in temperature difference between 200 m and the surface. From Rhein et al. (2013). Image from ipcc.ch.
Acceleration of the atmospheric hydrological cycle also affects ocean surface salinities (Figure \(\PageIndex{21}\)). Regions that are already salty such as the subtropics and the Atlantic get even saltier and regions that are already fresh like the North Pacific and the Southern Ocean get even fresher.
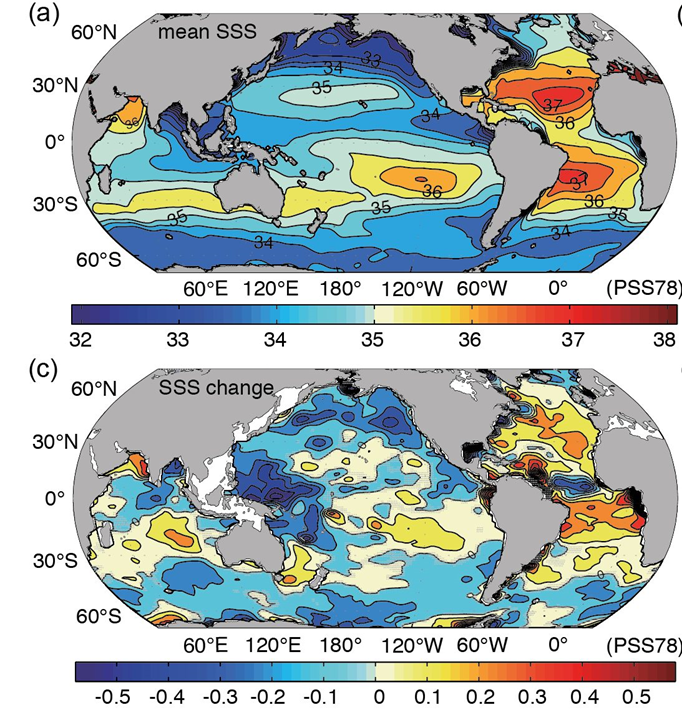
Figure \(\PageIndex{21}\): Surface ocean salinity (top) and salinity changes from 1950 to 2008 (bottom) in g/kg.
Warming and freshening of surface waters at high latitudes decreases their density and increases their buoyancy. This reduces deep water formation and the meridional overturning circulation. A reduction of the Atlantic meridional overturning circulation, which was initially predicted by climate models in the 1990’s (Manabe and Stouffer, 1993), is now observed in measurements from the subtropical Atlantic (Smeed et al., 2014). However, due to the relatively short period of the available data (2004 to the present) it is currently not clear how much of the observed reduction is caused by human greenhouse gas emissions and how much is due to natural variability. A long-term decline of the Atlantic meridional overturning circulation has been suggested by Rahmstorf et al. (2015) to cause the reduced warming over the subpolar North Atlantic in surface temperature observations (As shown here). Here is a nice interactive article about the topic.
Questions
- Why is it warmer at the equator than at the poles?
- Without heat transport in the atmosphere and oceans, how would temperatures be different at the equator and the poles?
- What determines the surface air pressure?
- What is the Hadley cell?
- How does the Hadley circulation influence precipitation patterns?
- What is the Intertropical Convergence Zone?
- From which direction blows the wind at the surface in the tropics, from which direction does it blow at mid-latitudes?
- In which direction does the Coriolis force acts in the northern and in the southern hemisphere?
- How does the Coriolis force impact the jet stream, the trade winds, and the westerly winds at mid-latitudes?
- What is latent heat of vaporization/condensation?
- How much more heat is required to vaporize water than to heat if from the melting to the boiling point?
- What is the lapse rate?
- How does vertical water vapor transport impact the lapse rate?
- When does evaporation occur?
- When does condensation occur?
- How much larger is the heat capacity of one cubic meter of water than one cubic meter of air?
- How does the difference in heat capacities of air and water impact climate variations?
- Which component of the climate system absorbs most of the energy that currently accumulates on Earth?
- Use the numbers in Fig. \(\PageIndex{14}\) to calculate the residence time of water in the atmosphere?
- Use the numbers in Fig. \(\PageIndex{14}\)to calculate the residence time of water in the ocean?
- In which direction do surface waters flow in the tropics, in which direction do they flow at mid-latitudes?
- What are the subtropical gyres, and what forces them.
- What is the strongest ocean current in the world?
- What is convergence, what is divergence? What does it imply for vertical flow (upwelling/downwelling)? Name one region each where surface ocean waters converge/diverge?
- What is stratification?
- What is the thermocline?
- What determines sea water density?
- What is the thermohaline circulation?
- Where do surface waters sink into the ocean’s interior?
- Where do they upwell back to the surface?
- Why is the Atlantic saltier than the Pacific?
- Where is the ocean warming the most?
- Is it possible that the warming observed in the atmosphere during the past 50 years was caused by changes in ocean circulation? Why?
- Where is the surface ocean becoming saltier, where fresher? How is the pattern of salinification/freshening related to the salinity of the surface ocean?
- How are changes in surface salinity related to changes in the atmospheric hydrological cycle?
References
Frierson, D. M. W., Y.-T. Hwang, N. S. Fuckar, R. Seager, S. M. Kang, A. Donohoe, E. A. Maroon, X. Liu, and D. S. Battisti (2013), Contribution of ocean overturning circulation to tropical rainfall peak in the Northern Hemisphere, Nature Geosci, 6(11), 940-944, doi:10.1038/ngeo1987.
Hartmann, D.L., A.M.G. Klein Tank, M. Rusticucci, L.V. Alexander, S. Brönnimann, Y. Charabi, F.J. Dentener, E.J. Dlugokencky, D.R. Easterling, A. Kaplan, B.J. Soden, P.W. Thorne, M. Wild and P.M. Zhai, 2013: Observations: Atmosphere and Surface. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T.F., D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P.M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Manabe, S., and R. J. Stouffer (1993), Century-Scale Effects of Increased Atmospheric CO2 on the Ocean-Atmosphere System, Nature, 364(6434), 215-218, doi: 10.1038/364215a0.
Peixoto, J., and A. Oort (1992) Physics of Climate, AIP Press.
Rahmstorf, S., J. E. Box, G. Feulner, M. E. Mann, A. Robinson, S. Rutherford, and E. J. Schaffernicht (2015), Exceptional twentieth-century slowdown in Atlantic Ocean overturning circulation, Nature Climate Change, 5(5), 475-480, doi: 10.1038/Nclimate2554.
Rhein, M., S.R. Rintoul, S. Aoki, E. Campos, D. Chambers, R.A. Feely, S. Gulev, G.C. Johnson, S.A. Josey, A. Kostianoy, C. Mauritzen, D. Roemmich, L.D. Talley and F. Wang, 2013: Observations: Ocean. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T.F., D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P.M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Smeed, D. A., G. D. McCarthy, S. A. Cunningham, E. Frajka-Williams, D. Rayner, W. E. Johns, C. S. Meinen, M. O. Baringer, B. I. Moat, A. Duchez, and H. L. Bryden (2014), Observed decline of the Atlantic meridional overturning circulation 2004-2012, Ocean Sci., 10(1), 29-38, doi: 10.5194/os-10-29-2014.
Trenberth, K. E., L. Smith, T. Qian, A. Dai, and J. Fasullo (2007), Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data, Journal of Hydrometeorology, 8(4), 758-769, doi:10.1175/jhm600.1.


