5.4: How can supersaturation be achieved?
- Page ID
- 3378
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Three basic mechanisms for cooling the air are RUM: Radiation, Uplift, and Mixing.
Radiation and mixing happen at constant pressure (isobaric); uplift happens at constant energy (adiabatic). Let’s consider these three cases in more detail. A good way to show what is happening is to use the water phase diagram. The video (3:15) entitled "Supersaturation Processes 2" below will explain these three processes in greater detail:
Supersaturation Processes 2
- Click here for transcript of the Supersaturation Processes 2 video.
-
Clouds will not form unless the air becomes supersaturated, meaning that its relative humidity is slightly greater than 100%. Or put it another way, it's supersaturation is greater than 0%. Let's look at the three ways that supersaturation can be achieved, radiative cooling, mixing, and adiabatic ascent. We can use the water phase diagram of water vapor on the y-axis versus temperature on the x-axis to examine these processes. Supersaturation means that the environment moves from the all-vapor part of the phase diagram into the all-liquid part by crossing the equilibrium line, which is given by the Clausius Clapeyron equation. I will mention only the essentials for each process, what changes and what stays the same. For radiative cooling, the water vapor pressure stays the same, but the temperature drops. And because the saturation vapor pressure depends only on temperature, the saturation vapor pressure also drops. The saturation vapor pressure decreases until it gets equal to and then a little less than the vapor pressure. And then the supersaturation above 0. The next process is mixing. Mixing clouds usually form when unsaturated, warm, moist air from a source is mixed into the unsaturated, colder, drier environmental air. As the warm, moist air mixes with the colder, drier air, the temperature and vapor pressure of the moist air parcel becomes the average of the temperature and vapor pressure of the moist, warm air parcel multiplied by the number of moles and the temperature and vapor pressure of the cold, dry environmental air multiplied by the number of moles, all this divided by the total number of moles. As the air parcel mixes with more environmental air, the parcel's temperature and vapor pressure move along the mixing line between the two initial air parcel states. If this line crosses the equilibrium line and goes into the liquid part of the phase diagram, supersaturation becomes greater than 0 and the cloud forms. If the air parcel continues to entrain the dry air, continues along the mixing line, and it may eventually cross the equilibrium line back into the vapor region, ant the cloud will evaporate. Contrails are one example of a mixing cloud. The contrail length tells you something about what the temperature and environmental pressure of the environmental air must be. The third process is adiabatic ascent. As an air parcel ascends, it's pressure and temperature drop. Because the water vapor mixing ratio is constant until a cloud forms, the drop in the pressure means a drop in the water vapor pressure. At the same time, a drop in the temperature means a drop in the saturation vapor pressure, which depends only on temperature. So vapor pressure and saturation vapor pressure are both dropping. However, in adiabatic ascent, the saturation vapor pressure drops faster than the vapor pressure, and eventually, they become equal. And then supersaturation becomes greater than 0, and the cloud forms.
Radiative Cooling
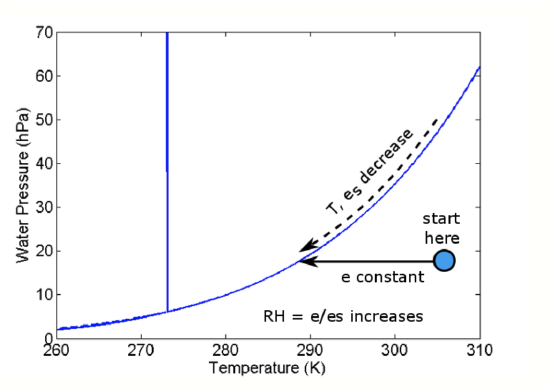
All matter radiates energy as electromagnetic waves, as we will see in the next lesson. When an air mass radiates this energy (mostly in the infrared part of the spectrum), it cools down, but the amount of water vapor does not change.
We can understand this process by using the water phase diagram (see figure below). Initially, the air mass is at the position of the blue dot. As the air parcel cools and the temperature drops, the air parcel temperature moves to the left on the diagram but the water vapor pressure does not change. However, because the temperature drops, es drops. When es becomes slightly less than e, a cloud forms.
Summary
- e is constant as T decreases.
- Since es depends only on T, es also decreases until es < e.
- When es becomes slightly less than e, a cloud forms.
An example of radiative cooling in action is radiation fog, which occurs overnight when Earth's surface and the air near it cool until a fog forms (see figure below).

Mixing
Assume two air parcels with different temperatures and water vapor partial pressures are at the same total pressure. If these two parcels mix, then the temperature and the water vapor partial pressure is going to be a weighted average of the T and e of the two parcels. The weighting is determined by the fraction of moles that each parcel contributes to the mixed parcel. Mathematically, for parcel 1 with e1, T1, and N1 (number of moles) and parcel 2 with e2, T2, and N2, the e and T of the mixed parcel are given by the equations:
\[e=\frac{N_{1}}{N_{1}+N_{2}} e_{1}+\frac{N_{2}}{N_{1}+N_{2}} e_{2}\] \[T=\frac{N_{1}}{N_{1}+N_{2}} T_{1}+\frac{N_{2}}{N_{1}+N_{2}} T_{2}\]
or approximately
\[e=\frac{M_{1}}{M_{1}+M_{2}} e_{1}+\frac{M_{2}}{M_{1}+M_{2}} e_{2}\] \[T=\frac{M_{1}}{M_{1}+M_{2}} T_{1}+\frac{M_{2}}{M_{1}+M_{2}} T_{2}\]
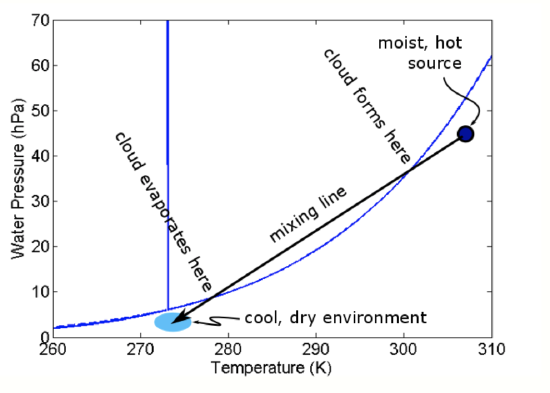
where M1 and M2 are the masses of the air parcels. On the phase diagram, these give straight lines for different proportions of the mixed parcel being from parcel 1 (0% to 100%) and parcel 2 (100% to 0%), as in the figure below.
Note that both of these two air parcels are unsaturated. So how does a cloud form? Think about a single warm, moist air parcel mixing into the environment of colder, drier air. As the warm mixes into more and more of the drier air, it gets increasingly diluted but the mixed parcel continues to grow. As the amount of environmental air in the mixture increases, the average e and T of the mixed air parcel decreases to be closer to the environmental values and the mixed parcel’s e and T follow a mixing line. Starting in the upper right near the warmer parcel, as the mixed parcel continues to grow, eventually the e and T will hit the Clausius-Clapeyron curve. As it continues to push into the liquid portion of the phase diagram and become supersaturated, a mixing cloud will form. The cloud will stay as long as the mixed e and T put the parcel to the left of the Clausius-Clapeyron curve. However, once the mixed parcel comes to the right of the curve, the cloud will evaporate.
Example:
Suppose air Parcel 1 has e = 20 hPa, T = 40oC, and N = 40,000 moles; and Parcel 2 has e = 5 hPa, T = 10oC, and N = 80,000 moles. Then using equation 5.4 (top):
\[e=\frac{40,0000}{40,000+80,000} 20+\frac{80,000}{40,00+80,000} 5=10 \mathrm{hPa}\]
\[T=\frac{40,000_{1}}{40,000+80,000} 40+\frac{80,000}{40,00+80,000} 10=20^{\circ} \mathrm{C}\]
There are many good examples of mixing clouds. One is a jet contrail; a second is your breath on a cold day; a third is a fog that forms when cold air moves over warm moist ground, say just after rain.

Uplift
The uplift of air can lead to cloud formation, as we know from the skew-T. Uplift is generally the same as adiabatic ascent. This adiabatic ascent can be driven by convection, by a less dense air mass overriding a more dense one, or by air flowing up and over a mountain. The following happens:
- The water vapor mixing ratio remains the same, but e drops as p drops, thus reducing the possibility that RH = e/es will reach 100%.
- The temperature drops in accordance with Poisson’s relations so that esalso drops.
The question is “Does e or es drop faster so that eventually e equals es?" It turns out that es drops faster. As a result, in uplifted air, e and es converge at the lifting condensation level (LCL) and a cloud forms just at that level (see figure below).
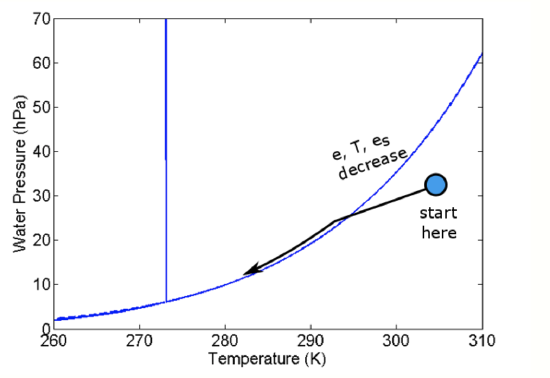
The arrow on the figure above shows the changes in e and T (and thus es) as an air parcel rises. Once es <= e, then s > 0 and the air parcel is supersaturated. This supersaturated situation is not stable; the water vapor in excess of es forms liquid. As the uplift continues, more water vapor is converted into liquid water and the vapor pressure remains close to es. All convective clouds, that is clouds with vertical extent, form this way. An example of adiabatic uplift is a cumulus cloud, as seen in the figure below.

Why is supersaturation required for a cloud drop to form?
I thought that cloud drops formed when \(w = w_s\). Why is supersaturation required for a cloud drop to form?
To answer this question, we need to look through a microscope at the nanometer scale, which is the scale of molecules and small particles. You all know that cloud condensation nuclei are needed for clouds to form, but do you know why? Watch the following video (3:16) entitled "Glory: The Cloud Makers."
Glory: The Cloud makers
- Click here for transcript of the Glory: The Cloud Makers video.
-
[music playing] NARRATOR: Aerosols are suspended throughout Earth's atmosphere, and the tiny, varied particles play a mysterious role in human induced climate change. Just like people, every aerosol particle is unique. Sometimes aerosols occur naturally, from things like volcanoes, but they can also originate from human activity. Aerosols are short-lived, but have an active lifetime! In just a short expanse of time, particles can change their size and composition and even travel across vast oceans. Aerosols are difficult to study, and one important new area of research involves how these particles impact clouds. Without aerosols, clouds could not exist. MICHAEL MISHCHENKO: An aerosol particle can serve as a cloud condensation nucleus. NARRATOR: The introduction of too many aerosols will modify a cloud's natural properties. MICHAEL MISHCHENKO: The more aerosol particles we have in the atmosphere, the more cloud droplets we can have. NARRATOR: Clouds play an important role in regulating Earth's climate; aerosol-rich clouds become bigger, brighter, and longer lasting. Aerosols impact clouds in other ways. Some aerosol particles primarily reflect solar radiation and cool the atmosphere, and others absorb radiation, which warms the air. When aerosols heat the atmosphere, they create an environment where clouds can't thrive. The suppression of clouds leads to further warming of the atmosphere by solar radiation. Researchers are still working to understand the role of these curious particles. MICHAEL MISHCHENKO: We need to study the distribution of particles globally, and the only way to do that is from satellites. NARRATOR: New tools will soon help scientists study aerosols. The Aerosol Polarimetry Sensor, or APS, is among a suite of instruments onboard NASA's upcoming Glory mission. The APS will provide a global dataset of aerosol distribution with unprecedented accuracy and specificity. Unique data from the Glory mission, along with NASA's fleet of Earth observing satellites, will help researchers investigate the intricacies of Earth's changing climate. [music playing] [wind blowing] Credit: NASA
In the atmosphere, relative humidity rarely rises much above 100% because small aerosol particles act as Cloud Condensation Nuclei (CCN). Two effects most strongly determine the amount of supersaturation that each particle must experience in order to accumulate enough water to grow into a cloud drop. The first is a physical effect of curvature on increasing the water vapor equilibrium pressure; the second is a chemical effect of the aerosol dissolving in the growing water drop and reducing its vapor equilibrium pressure. You will learn about these two effects in the next two sections of this lesson.


